Signo de la función
De Wikillerato
(Página nueva: <br/> ==Introducción== <br/> En muchos casos, es interesante el conocer el signo que toma la función <math> \mathrm{f} \left( \, x \, \right) </math> dependiendo de...) |
|||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 33: | Línea 33: | ||
<br/> | <br/> | ||
| - | + | Supongamos tambien que existe una función | |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
| Línea 48: | Línea 48: | ||
<br/> | <br/> | ||
| - | + | En este caso, a los propietarios y empleados de la compañia les interesaría mucho saber para que | |
valores de | valores de | ||
<math> | <math> | ||
| Línea 68: | Línea 68: | ||
<br/> | <br/> | ||
| - | ==Signo de la función y grafica== | + | ==Signo de la función y su grafica== |
<br/> | <br/> | ||
| Línea 97: | Línea 97: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \mathrm{f} \left( \, x \, \right) | + | 0 > \mathrm{f} \left( \, x \, \right) |
</math> | </math> | ||
</center> | </center> | ||
| - | + | Si uno no tiene mucha habilidad para resolver inecuaciones, | |
| - | puede utilizar el método que se describe mas abajo. | + | puede, alternativamente, utilizar el método que se describe mas abajo. |
<br/> | <br/> | ||
| Línea 124: | Línea 124: | ||
Supongamos que las abcisas de los puntos de corte con el eje X y de los puntos | Supongamos que las abcisas de los puntos de corte con el eje X y de los puntos | ||
| - | de discontinuidad son, | + | de discontinuidad son, ordenadas de menor a mayor |
<center> | <center> | ||
<math> | <math> | ||
| Línea 130: | Línea 130: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | Estas dividen a la recta real en | |
<math> | <math> | ||
n + 1 | n + 1 | ||
| Línea 193: | Línea 193: | ||
<br/> | <br/> | ||
| - | + | Finalmente, en cada uno de los puntos de discontinuidad donde este definida la función, evaluamos el signo de | |
<math> | <math> | ||
f | f | ||
</math> | </math> | ||
| - | en dicho punto | + | en dicho punto. |
| + | |||
| + | <br/> | ||
| + | |||
| + | Con este ultimo paso terminariamos el estudio del signo y sabriamos para que | ||
| + | valores de | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | para | + | es positiva y |
| + | para que | ||
| + | valores de | ||
<math> | <math> | ||
x | x | ||
</math> | </math> | ||
| - | |||
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| + | es negativa. | ||
| + | |||
| + | [[Categoría: Matemáticas]] | ||
Revisión actual
Tabla de contenidos |
Introducción
En muchos casos, es interesante el conocer el signo que toma la función
 dependiendo de los valores de
dependiendo de los valores de
 .
.
Ejemplo
Supongamos que la variable dependiente
 son los beneficios de una compañia en un año cualquiera. Resulta que estos beneficios
dependen de los ingresos de la compañia a lo largo del año y que representaremos
por
son los beneficios de una compañia en un año cualquiera. Resulta que estos beneficios
dependen de los ingresos de la compañia a lo largo del año y que representaremos
por
 .
.
Supongamos tambien que existe una función
 que establece de manera precisa como depende
que establece de manera precisa como depende
 de
de
 .
.
En este caso, a los propietarios y empleados de la compañia les interesaría mucho saber para que
valores de

 toma valores negativos ( perdidas ) y para que
valores de
toma valores negativos ( perdidas ) y para que
valores de

 toma valores positivos ( ganancias ).
toma valores positivos ( ganancias ).
Signo de la función y su grafica
Para encontrar los valores de
 para los cuales
para los cuales
 es positiva, podemos resolver la inecuación
es positiva, podemos resolver la inecuación
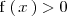
y para encontrar los valores de
 para los cuales
para los cuales
 es negativa, podemos resolver la inecuación
es negativa, podemos resolver la inecuación
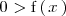
Si uno no tiene mucha habilidad para resolver inecuaciones, puede, alternativamente, utilizar el método que se describe mas abajo.
Procedimiento de análisis del signo
En primer lugar, hallamos los puntos de corte de la grafica de la
función
 con el eje X y lo puntos de discontinuidad de
con el eje X y lo puntos de discontinuidad de
 .
.
Supongamos que las abcisas de los puntos de corte con el eje X y de los puntos de discontinuidad son, ordenadas de menor a mayor
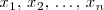
Estas dividen a la recta real en
 intervalos:
intervalos:
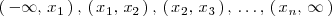
En cada uno de estos intervalos escogemos un
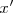 y evaluamos
y evaluamos
 en el.
en el.
Si
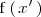 es positivo, entonces
es positivo, entonces
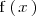 es positivo para todo
es positivo para todo
 en el intervalo donde hemos cogido
en el intervalo donde hemos cogido
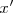 .
.
Reciprocamente, si
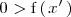 ,
entonces
,
entonces
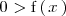 para todo
para todo
 en el intervalo donde hemos cogido
en el intervalo donde hemos cogido
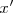 .
.
Finalmente, en cada uno de los puntos de discontinuidad donde este definida la función, evaluamos el signo de
 en dicho punto.
en dicho punto.
Con este ultimo paso terminariamos el estudio del signo y sabriamos para que
valores de

 es positiva y
para que
valores de
es positiva y
para que
valores de

 es negativa.
es negativa.



