Aceleración
De Wikillerato
(→Casos particulares) |
|||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | Llamamos aceleración <math>\vec a</math> a la variación temporal del vector velocidad, es decir: | + | Llamamos '''aceleración''' (<math>\vec a</math>) a la variación temporal del [[vector]] [[Concepto de velocidad|velocidad]], es decir: |
<math>\vec a = \frac{\Delta\vec v}{\Delta t}</math> | <math>\vec a = \frac{\Delta\vec v}{\Delta t}</math> | ||
| - | En el caso en el que la variación de la velocidad no sea constante, al cociente | + | En el caso en el que la variación de la velocidad no sea [[constante]], al [[cociente]] |
<math> a = \frac{\Delta v}{\Delta t}</math> | <math> a = \frac{\Delta v}{\Delta t}</math> | ||
| - | se le denomina aceleración media. | + | se le denomina '''aceleración media'''. |
| - | En este caso, si consideramos intervalos de tiempo instantáneos, podremos hablar de aceleración instantánea y se podrá definir mediante la ecuación, | + | En este caso, si consideramos intervalos de [[tiempo]] instantáneos, podremos hablar de '''aceleración instantánea''' y se podrá definir mediante la [[ecuación]], |
<math>\vec a = \lim_{\Delta t\to 0} \frac{\Delta\vec v}{\Delta t} = \frac{d\vec v}{dt}</math> | <math>\vec a = \lim_{\Delta t\to 0} \frac{\Delta\vec v}{\Delta t} = \frac{d\vec v}{dt}</math> | ||
| - | La aceleración media es un escalar, pues no podemos atribuirle una dirección, dado que la variación temporal de v no es constante. Sin embargo, la aceleración instantánea es una magnitud vectorial, pues nos proporciona las variaciones del vector velocidad en un instante preciso. En el | + | La aceleración media es un [[escalar]], pues no podemos atribuirle una [[dirección]], dado que la variación temporal de <math>v</math> no es constante. Sin embargo, la aceleración instantánea es una [[magnitud]] vectorial, pues nos proporciona las variaciones del vector velocidad en un instante preciso. En el '''[[Sistema Internacional|S.I.]]''' la unidad en que se expresa la aceleración es <math>m s^{-2}</math>, pues se obtiene de dividir una diferencia de velocidades entre un tiempo preciso, <math> m s^{-1}/s</math>. |
Teniendo en cuenta que: | Teniendo en cuenta que: | ||
| - | <math> \vec v = v_x\vec i + v_y\vec j + v_z\vec k</math> | + | <math> \vec v = v_x\vec i + v_y \vec j + v_z \vec k </math> |
si derivamos, se obtiene: | si derivamos, se obtiene: | ||
| - | <math>\vec a = \frac{d ( v_x\vec i + v_y\vec j + v_z\vec k)}{dt}</math> | + | <math> |
| + | \vec a = \frac{d ( v_x\vec i + v_y\vec j + v_z\vec k)}{dt} | ||
| + | </math> | ||
<math>\vec a = \frac{d v_x}{dt} \vec i+ \frac{d v_y}{dt} \vec j + \frac{d v_z}{dt} \vec k</math> | <math>\vec a = \frac{d v_x}{dt} \vec i+ \frac{d v_y}{dt} \vec j + \frac{d v_z}{dt} \vec k</math> | ||
| - | con lo cual: | + | con lo cual:: |
| - | <math> \vec a = a_x\vec i + a_y\vec j + a_z\vec k</math> | + | <math> \vec a = a_x \vec i + a_y \vec j + a_z \vec k</math> |
| - | Que es la expresión de la aceleración en un instante dado en función de sus componentes en un sistema ortogonal tridimensional. | + | Que es la [[expresión]] de la aceleración en un instante dado en función de sus componentes en un [[sistema ortogonal tridimensional]]. |
| - | Desde un punto de | + | Desde un punto de vista analítico se podrá escribir también: |
<math>\vec a = \frac{d\vec v}{d t} = \frac{\frac {d\vec r}{dt}}{dt}</math>, | <math>\vec a = \frac{d\vec v}{d t} = \frac{\frac {d\vec r}{dt}}{dt}</math>, | ||
| - | o lo que es igual <math>\vec a = \frac{d^2\vec r}{d t^2} </math>. | + | o lo que es igual <math>\vec a = \frac{d^2\vec r}{d t^2} </math>. |
Es decir, el resultado de derivar con respecto al tiempo el vector <math>\vec r</math> dos veces consecutivas, que se leerá como la derivada segunda de <math>\vec r</math> con respecto de <math>t</math> dos veces. | Es decir, el resultado de derivar con respecto al tiempo el vector <math>\vec r</math> dos veces consecutivas, que se leerá como la derivada segunda de <math>\vec r</math> con respecto de <math>t</math> dos veces. | ||
| + | |||
| + | ====Casos particulares==== | ||
| + | |||
| + | a) Si el [[movimiento]] se encuentra contenido en un [[plano]], podremos escribir: | ||
| + | |||
| + | <math> \vec a = a_x\vec i + a_y\vec j </math> | ||
| + | |||
| + | siendo <math> a_x</math> y <math> a_y</math> las componentes de la aceleración en sistemas de coordenadas cartesiano. | ||
| + | |||
| + | b) Cuando se trata de un [[movimiento rectilíneo]], tendremos | ||
| + | |||
| + | <math> \vec a = a\vec u_r </math> | ||
| + | |||
| + | siendo <math> \vec u_r </math> el [[vector unitario]] en la dirección de la [[recta]] que soporta el movimiento. | ||
| + | |||
| + | En este caso, podremos hablar de un movimiento rectilíneo acelerado, y si a es constante con respecto al tiempo, hablaremos de un '''movimiento rectilíneo uniformemente acelerado'''. La aceleración podrá ser positiva, si hace aumentar la velocidad en cada instante, o negativa, si la hace disminuir. | ||
| + | |||
| + | == Véase también == | ||
| + | # [[Movimiento rectilíneo]] | ||
| + | |||
| + | [[Category: Física]] | ||
Revisión actual
Llamamos aceleración (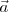 ) a la variación temporal del vector velocidad, es decir:
) a la variación temporal del vector velocidad, es decir:
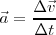
En el caso en el que la variación de la velocidad no sea constante, al cociente
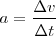
se le denomina aceleración media.
En este caso, si consideramos intervalos de tiempo instantáneos, podremos hablar de aceleración instantánea y se podrá definir mediante la ecuación,
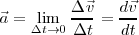
La aceleración media es un escalar, pues no podemos atribuirle una dirección, dado que la variación temporal de  no es constante. Sin embargo, la aceleración instantánea es una magnitud vectorial, pues nos proporciona las variaciones del vector velocidad en un instante preciso. En el S.I. la unidad en que se expresa la aceleración es
no es constante. Sin embargo, la aceleración instantánea es una magnitud vectorial, pues nos proporciona las variaciones del vector velocidad en un instante preciso. En el S.I. la unidad en que se expresa la aceleración es 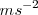 , pues se obtiene de dividir una diferencia de velocidades entre un tiempo preciso,
, pues se obtiene de dividir una diferencia de velocidades entre un tiempo preciso, 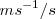 .
.
Teniendo en cuenta que:
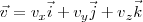
si derivamos, se obtiene:
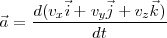
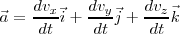
con lo cual::
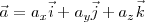
Que es la expresión de la aceleración en un instante dado en función de sus componentes en un sistema ortogonal tridimensional.
Desde un punto de vista analítico se podrá escribir también:
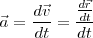 ,
,
o lo que es igual 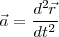 .
.
Es decir, el resultado de derivar con respecto al tiempo el vector 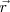 dos veces consecutivas, que se leerá como la derivada segunda de
dos veces consecutivas, que se leerá como la derivada segunda de 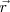 con respecto de
con respecto de  dos veces.
dos veces.
Casos particulares
a) Si el movimiento se encuentra contenido en un plano, podremos escribir:
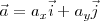
siendo 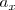 y
y 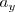 las componentes de la aceleración en sistemas de coordenadas cartesiano.
las componentes de la aceleración en sistemas de coordenadas cartesiano.
b) Cuando se trata de un movimiento rectilíneo, tendremos
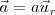
siendo 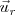 el vector unitario en la dirección de la recta que soporta el movimiento.
el vector unitario en la dirección de la recta que soporta el movimiento.
En este caso, podremos hablar de un movimiento rectilíneo acelerado, y si a es constante con respecto al tiempo, hablaremos de un movimiento rectilíneo uniformemente acelerado. La aceleración podrá ser positiva, si hace aumentar la velocidad en cada instante, o negativa, si la hace disminuir.



