Primitiva de una función
De Wikillerato
(→Definición) |
(→Definición) |
||
| Línea 1: | Línea 1: | ||
| + | |||
==Definición== | ==Definición== | ||
| Línea 28: | Línea 29: | ||
\mathrm{f} \left( \, x \, \right) | \mathrm{f} \left( \, x \, \right) | ||
</math> | </math> | ||
| - | si la derivada de | + | si la [[Definici\'on de derivada|derivada]] de |
<math> | <math> | ||
\mathrm{F} \left( \, x \, \right) | \mathrm{F} \left( \, x \, \right) | ||
| Línea 41: | Línea 42: | ||
</math> | </math> | ||
. | . | ||
| + | |||
| + | <br/> | ||
<center> | <center> | ||
| Línea 59: | Línea 62: | ||
Calcular la primitiva de una función es el proceso inverso al de calcular su derivada. | Calcular la primitiva de una función es el proceso inverso al de calcular su derivada. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Ejemplo== | ||
| + | |||
| + | <br/> | ||
Consideremos la función: | Consideremos la función: | ||
| Línea 64: | Línea 73: | ||
<math> f(x) = x^2 \, </math>. | <math> f(x) = x^2 \, </math>. | ||
| - | Su derivada | + | Su derivada es: |
| - | <math> | + | <center> |
| + | <math> | ||
| + | \mathrm{f}^\prime \left( \,x \, \right) \, = \, 2 \cdot x | ||
| + | </math> | ||
| + | </center> | ||
por lo que la primitiva de <math>g(x) \,</math> que denotaremos como <math>\int g(x)\, </math> es igual a: | por lo que la primitiva de <math>g(x) \,</math> que denotaremos como <math>\int g(x)\, </math> es igual a: | ||
Revisión de 14:47 10 mar 2008
Definición
Dadas dos funciones
 y
y
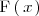 , definidas en un intervalo
, definidas en un intervalo
![</p>
<pre>I =
</pre>
<p>\left[
</p>
<pre> \, a, \, b \,
</pre>
<p>\right]
</p>
<pre>I =
</pre>
<p>\left[
</p>
<pre> \, a, \, b \,
</pre>
<p>\right]](/images/math/math-ec1b2022a1621b88d0396b296196a49e.png) , diremos que
, diremos que
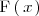 es una función primitiva de
es una función primitiva de
 si la derivada de
si la derivada de
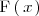 es la función
es la función
 en el intervalo
en el intervalo
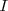 .
.
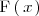 es primitiva de
es primitiva de
 en
[Unparseable or potentially dangerous latex formula. Error 3 ]
en
[Unparseable or potentially dangerous latex formula. Error 3 ]
Calcular la primitiva de una función es el proceso inverso al de calcular su derivada.
Ejemplo
Consideremos la función:
[Unparseable or potentially dangerous latex formula. Error 3 ].
Su derivada es:
[Unparseable or potentially dangerous latex formula. Error 3 ]
por lo que la primitiva de [Unparseable or potentially dangerous latex formula. Error 3 ] que denotaremos como [Unparseable or potentially dangerous latex formula. Error 3 ] es igual a:
[Unparseable or potentially dangerous latex formula. Error 3 ].
Sin embargo, el resultado anterior es sólo parcialmente correcto. El problema es que la inversa de la derivada no es única. Si os dais cuenta, podemos sumar a 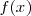 una constante y su derivada no cambiará.
una constante y su derivada no cambiará.
Por lo tanto si:
[Unparseable or potentially dangerous latex formula. Error 3 ],
tenemos que
[Unparseable or potentially dangerous latex formula. Error 3 ],
donde  es una constante.
es una constante.



