Buscar en WikilleratO
Temario:
Seleccionar asignatura
Matemáticas
Física
Filosofía
Lengua y Literatura
Dibujo Técnico
Historia
Historia del Arte
Química
Biología
Límite de una función
De Wikillerato
(Diferencias entre revisiones)
Línea 1:
Línea 1: - %% {{{ =limite
-
El límite de la función
El límite de la función
<math>
<math>
Línea 192:
Línea 190: </math>
</math>
lo suficientemente pequeño.
lo suficientemente pequeño.
-
- <br/>
-
- [[Category:Matemáticas]]
-
- %% }}}
- %% {{{ =continuidad de funciones
-
- Una función
- <math>
- \mathrm{f}
- </math>
- es '''''continua''''' en el punto
- <math>
- x \, = \, x_0
- </math>
- si
- <math>
- \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) \, = \,
- \mathrm{f} \left( \, x_0 \, \right)
- </math>.
-
- <br/>
-
- El que una función
- <math>
- \mathrm{f}
- </math>
- sea continua en el punto
- <math>
- x \, = \, x_0
- </math>
- implica que
- <math>
- \mathrm{f} \left( \, x_0 \, \right)
- </math>
- existe y que
- <math>
- \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right)
- </math>
- tambien existe.
-
- <br/>
-
- Una función es '''''continua en un intervalo''''' si es continua en todos los puntos del
- intervalo.
-
- <br/>
-
- Una función es '''''continua en todo su dominio''''' cuando lo es en todos los puntos que
- lo componen.
-
- <br/>
-
- [[Category:Matemáticas]]
-
- %% }}}
- %% {{{ =discontinuidades
- ==Definición==
-
- <br/>
-
- Una función es '''''discontinua''''' en un punto
- <math>
- x \, = \, x_0
- </math>
- si
- <math>
- \mathrm{f}
- </math>
- no es continua en dicho punto.
-
- <br/>
-
- ==Tipos de discontinuidades==
-
- <br/>
-
- ===Discontinuidad evitable===
-
- <br/>
-
- Una función
- <math>
- \mathrm{f}
- </math>
- tiene una '''''discontinuidad evitable''''' en un punto
- <math>
- x \, = \, x_0
- </math>
- cuando existe el limite de la función en dicho punto.
-
- <br/>
-
- ====Ejemplo====
-
- <br/>
-
- La función
- <math>
- \mathrm{f}
- </math>
- definida por:
-
- <br/>
-
- <center>
- <math>
- \mathrm{f} \left( \, x \, \right) \, = \,
- \left\{
- \begin{array}[c]{rcl}
- \frac{\displaystyle x^2 \, - \, 1}{\displaystyle x \, - \, 1} & , &
- \quad \makebox{si}\quad x \neq 1
- \\
- 3 & , & \quad \makebox{si} \quad x \, = \, 1
- \end{array}
- \right.
- </math>
- </center>
-
- <br/>
-
- no es continua en el punto
- <math>
- x \, = \, 1
- </math>
- porque
- <math>
- \lim_{x \to 1} \mathrm{f} \left( \, x \, \right) \, = \, 2
- </math>
- mientras que
- <math>
- \mathrm{f} \left( \, 1 \, \right) \, = \, 3
- </math>
- , es decir:
-
- <br/>
-
- <center>
- <math>
- \lim_{x \to 1} \mathrm{f} \left( \, x \, \right) \, \neq \,
- \mathrm{f} \left( \, 1 \, \right)
- </math>
- </center>
-
- <br/>
-
- Como
- <math>
- \lim_{x \to 1} \mathrm{f} \left( \, x \, \right)
- </math>
- existe, la discontinuidad que
- <math>
- \mathrm{f}
- </math>
- tiene en el punto
- <math>
- x \, = \, 1
- </math>
- es evitable.
-
- <br/>
-
- ===Discontinuidad de primera especie===
-
- <br/>
-
- Una función presenta una '''''discontinuidad de primera especie''''' en el punto
- <math>
- x \, = \, x_0
- </math>
- si los limites laterales de
- <math>
- f
- </math>
- en
- <math>
- x \, = \, x_0
- </math>
- existen pero son distintos, es decir:
-
- <br/>
-
- <center>
- <math>
- \lim_{x \to x_0^+} \mathrm{f} \left( \, x \, \right) \, \neq \,
- \lim_{x \to x_0^-} \mathrm{f} \left( \, x \, \right)
- </math>
- </center>
-
- <br/>
-
- ====Ejemplo====
-
- <br/>
-
- La función
- <math>
- \mathrm{f}
- </math>
- definida por:
-
- <br/>
-
- <center>
- <math>
- \mathrm{f} \left( \, x \, \right) \, = \,
- \left\{
- \begin{array}[c]{rcl}
- x^2 \, + \, 1 & , & \quad \makebox{si} \quad 1 \ge x
- \\
- x \, - \, 1 & , & \quad \makebox{si} \quad x \, > \, 1
- \end{array}
- \right.
- </math>
- </center>
-
- <br/>
-
- no es continua en el punto
- <math>
- x \, = \, 1
- </math>
- porque
- <math>
- \lim_{x \to 1} \mathrm{f} \left( \, x \, \right)
- </math>
- no existe, al ser ambos limites laterales distintos:
-
- <br/>
-
- <center>
- <math>
- \lim_{x \to 1^+} \mathrm{f} \left( \, x \, \right) \, = \, 0
- </math>
-
- <br/>
-
- <math>
- \lim_{x \to 1^-} \mathrm{f} \left( \, x \, \right) \, = \, 2
- </math>
- </center>
-
- <br/>
-
- Como ambos limites laterales existen, la discontinuidad que
- <math>
- \mathrm{f}
- </math>
- tiene en el punto
- <math>
- x \, = \, 1
- </math>
- es de primera especie.
-
- <br/>
-
- ===Discontinuidad de segunda especie===
-
- <br/>
-
- Una función
- <math>
- f
- </math>
- presenta una '''''discontinuidad de segunda especie''''' en el punto
- <math>
- x \, = \, x_0
- </math>
- si no existe alguno de los limites laterales de
- <math>
- f
- </math>
- en dicho punto.
-
- <br/>
-
- ====Ejemplo====
-
- <br/>
-
- La función
- <math>
- \mathrm{f}
- </math>
- definida por:
-
- <br/>
-
- <center>
- <math>
- \mathrm{f} \left( \, x \, \right) \, = \,
- \left\{
- \begin{array}[c]{rcl}
- \frac{1}{x} & , & \quad \makebox{si} \quad 0 \ge x
- \\
- 1 & , & \quad \makebox{si} \quad x \, > \, 0
- \end{array}
- \right.
- </math>
- </center>
-
- <br/>
-
- no es continua en el punto
- <math>
- x \, = \, 0
- </math>
- porque
- <math>
- \lim_{x \to 0} \mathrm{f} \left( \, x \, \right)
- </math>
- no existe, al no existir el limite por la izquierda de
- <math>
- \mathrm{f}
- </math>
- cuando
- <math>
- x \to 0
- </math>:
-
- <br/>
-
- <center>
- <math>
- \lim_{x \to 0^-} \mathrm{f} \left( \, x \, \right) \, = \, -\infty
- </math>
- </center>
-
- <br/>
-
- Como este limite por la izquierda no existe
- <math>
- \mathrm{f}
- </math>
- tiene en el punto
- <math>
- x \, = \, 0
- </math>
- una discontinuidad de segunda especie.
<br/>
<br/>
[[Category:Matemáticas]]
[[Category:Matemáticas]]
Revisión de 15:06 11 ene 2007
El límite de la función
límites laterales existen y son iguales a
Lo expresamos de la siguiente manera:
El que la anterior igualdad sea cierta significa que podemos hacer
Se dice que el límite de la funcion
Lo expresamos como:
[Unparseable or potentially dangerous latex formula. Error 3 ]
El que la anterior igualdad sea cierta significa que podemos hacer
Analogamente, se dice que el límite de la funcion
Lo expresamos como:
El que la anterior igualdad sea cierta significa que podemos hacer
Los contenidos de
Wikillerato están disponibles bajo una
licencia de Creative Commons .
Pueden utilizarse y redistribuirse libremente siempre que se reconozca su procedencia.
 , cuando
, cuando
 tiende a
tiende a
 existe y es igual a
existe y es igual a
 , si ambos límites laterales existen y son iguales a
, si ambos límites laterales existen y son iguales a
 , es decir
, es decir
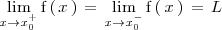
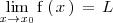
 tan cercano a
tan cercano a
 como queramos eligiendo
como queramos eligiendo
 lo suficientemente proximo a
lo suficientemente proximo a
 , por la derecha o por la izquierda.
, por la derecha o por la izquierda.
 , cuando
, cuando
 tiende a
tiende a
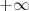 , es
, es
 si cualquier sucesión
si cualquier sucesión
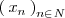 que tiende a
que tiende a
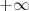 verifica que
verifica que
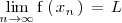 .
.
 tan cercano a
tan cercano a
 como queramos eligiendo
como queramos eligiendo
 lo suficientemente grande.
lo suficientemente grande.
 , cuando
, cuando
 tiende a
tiende a
 , es
, es
 si cualquier sucesión
si cualquier sucesión
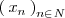 que tiende a
que tiende a
 verifica que
verifica que
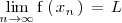 .
.
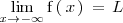
 tan cercano a
tan cercano a
 como queramos eligiendo
como queramos eligiendo
 lo suficientemente pequeño.
lo suficientemente pequeño.



