Razones trigonométricas de la suma y diferencia de ángulos
De Wikillerato
(Diferencias entre revisiones)
m (Revertidas las ediciones realizadas por 190.14.227.187 (Talk); a la última edición de 213.97.196.225) |
|||
| (8 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | + | Se puede demostrar que dados dos angulos | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
\alpha | \alpha | ||
</math> | </math> | ||
| - | | + | y |
<math> | <math> | ||
| - | + | \beta | |
</math> | </math> | ||
| - | + | , el seno de su suma viene dado por la formula: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
<center> | <center> | ||
| Línea 281: | Línea 93: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | El coseno de la suma de los angulos | ||
| + | <math> | ||
| + | \alpha | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | \beta | ||
| + | </math> | ||
| + | viene dado por la formula: | ||
<br/> | <br/> | ||
| Línea 369: | Línea 193: | ||
<br/> | <br/> | ||
| + | La segunda igualdad es cierta por las relaciones entre las razones trigonometricas de | ||
| + | | ||
| + | <math> | ||
| + | \alpha | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | -\alpha | ||
| + | </math>: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{cos} | ||
| + | \left( | ||
| + | \, -\alpha \, | ||
| + | \right) | ||
| + | \, = \, \mathrm{cos} | ||
| + | \left( | ||
| + | \, \alpha \, | ||
| + | \right) | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | \mathrm{sen} | ||
| + | \left( | ||
| + | \, -\alpha \, | ||
| + | \right) | ||
| + | \, = \, -\mathrm{sen} | ||
| + | \left( | ||
| + | \, \alpha \, | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si te preguntas porque esto es así, puedes encontrar la respeusta en [[Reducción de las razones trigonometricas]]. | ||
| + | |||
| + | <br/> | ||
| + | |||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión actual
Se puede demostrar que dados dos angulos
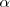 y
y
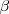 , el seno de su suma viene dado por la formula:
, el seno de su suma viene dado por la formula:
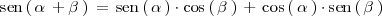
Si en la formula anterior sustituimos
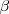 por
por
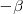 obtenemos:
obtenemos:
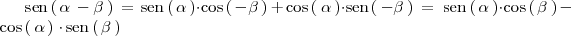
El coseno de la suma de los angulos
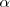 y
y
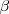 viene dado por la formula:
viene dado por la formula:
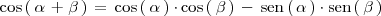
Si en la formula anterior sustituimos
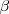 por
por
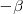 obtenemos:
obtenemos:
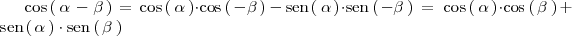
La segunda igualdad es cierta por las relaciones entre las razones trigonometricas de
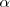 y
y
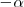 :
:
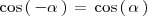
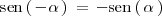
Si te preguntas porque esto es así, puedes encontrar la respeusta en Reducción de las razones trigonometricas.



