Navegación
Herramientas
La divisibilidad en los polinomios
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| + | |||
==Definición de polinomio DIVISIBLE por otro== | ==Definición de polinomio DIVISIBLE por otro== | ||
| Línea 114: | Línea 115: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \begin{array}{ | + | \begin{array}{l} |
| - | \mathrm{P} \left( \, x \, \right) | + | \mathrm{P} \left( \, x \, \right) = x - 3 |
\\ | \\ | ||
| - | \mathrm{Q} \left( \, x \, \right) | + | \mathrm{Q} \left( \, x \, \right) = x^2 + x + 1 |
\end{array} | \end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
Revisión de 08:17 19 sep 2010
Tabla de contenidos[ocultar] |
Definición de polinomio DIVISIBLE por otro
Un polinomio
es divisible por otro polinomio
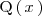cuando existe otro polinomio
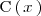tal que
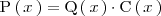
Los polinomios
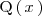y
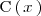se llaman divisores de
.
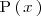Ejemplo
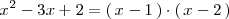
Por lo tanto el polinomio
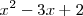es divisible por los polinomios
y
,
o dicho de otra manera, los polinomios
y
son divisores del polinomio
.
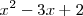Definición de polinomio IRREDUCIBLE
Un polinomio
de grado
se dice que es irreducible cuando ningún polinomio de grado
menor que
y mayor que 0 es divisor de
.
Cualquier polinomio que no sea irreducible se puede descomponer en forma de producto de polinomios irreducibles.
Ejemplos
Los siguientes dos polinomios son irreducibles:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Tweet
