Navegación
Herramientas
Integral indefinida
De Wikillerato
(Diferencias entre revisiones)
(→Ejemplo) |
(→Ejemplo) |
||
| (5 ediciones intermedias no se muestran.) | |||
| Línea 58: | Línea 58: | ||
El simbolo | El simbolo | ||
| - | <math> | + | <math>\int \quad\quad</math> |
| - | \int | + | |
| - | </math> | + | |
se lee "integral de". | se lee "integral de". | ||
| Línea 95: | Línea 93: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \int 2 \,u \,x \ | + | \int 2 \,u \,x \,\, \mathrm{d}x \, = \, x^2 \cdot u \, + \, C \quad |
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | [[Categoría:Matemáticas]] | ||
Revisión actual
Definición
Sea
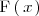una primitiva de
en el intervalo
![I \, = \,
\left[
</p>
<pre> \, a, \, b \,
</pre>
<p>\right]](/images/math/math-0bfe901292fdbe15ae4c584db65bec48.png "I \, = \,
\left[
</p>
<pre> \, a, \, b \,
</pre>
<p>\right]")
. Llamamos integral indefinida de
al conjunto de todas sus primitivas, y lo representamos por:
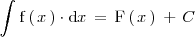
Para cada valor de
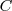existe una primitiva de
.
La constante
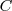recibe el nombre de constante de integración.
El simbolo
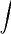se lee "integral de".
A la función
se le llama integrando.
La exprexión
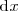nos indica que buscamos la primitiva de la función
con respecto a la variable
. De esta forma, cualquier otra variable que aparezca en el integrando se considerara como una constante.
Ejemplo
Tweet
