Funciones acotadas
De Wikillerato
89.7.158.180 (Discutir)
(Página nueva: ==Definición== <br/> Se dice que un conjunto <math> A </math> de números reales esta acotado superiormente ( inferiormente ) si existe un número real que es mayor ( menor )...)
Ir a las siguientes diferencias →
Revisión de 09:44 31 jul 2010
Tabla de contenidos[ocultar] |
Definición
Se dice que un conjunto
 de números reales esta acotado superiormente ( inferiormente ) si existe un
número real que es
mayor ( menor ) o igual que todos los elementos de
de números reales esta acotado superiormente ( inferiormente ) si existe un
número real que es
mayor ( menor ) o igual que todos los elementos de
 .
.
Ejemplo
El intervalo
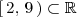
es un conjunto acotado superiormente porque
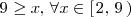
Tambien esta acotado inferiormente porque
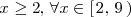
Definición
Una función
 esta acotada superiormente si su recorrido esta acotado superiormente, es decir,
si existe un número
esta acotada superiormente si su recorrido esta acotado superiormente, es decir,
si existe un número
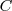 tal que
tal que
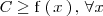 en el dominio de
en el dominio de

Analogamente,
 esta acotada inferiormente si su recorrido esta acotado inferiormente, es decir,
si existe un número
esta acotada inferiormente si su recorrido esta acotado inferiormente, es decir,
si existe un número
 tal que
tal que
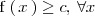 en el dominio de
en el dominio de

Una función acotada es aquella que esta acotada superior e inferiormente.
Ejemplo
El recorrido de la función
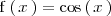 es el intervalo cerrado
es el intervalo cerrado
![\left[ \, -1, \, 1 \, \right]
\left[ \, -1, \, 1 \, \right]](/images/math/math-835b91871a82c41933594d58cb622152.png) .
Como este intervalo esta acotado, tanto superior como inferiormente,
la función
.
Como este intervalo esta acotado, tanto superior como inferiormente,
la función
 esta acotada tanto superior como inferiormente, es decir, la función
esta acotada tanto superior como inferiormente, es decir, la función
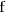 esta acotada.
esta acotada.
Propiedades
Propiedad 1
En la grafica de
 , el que
, el que
 este acotada superiormente ( inferiormente ) se traduce en que existe una linea horizontal (
paralela al eje
este acotada superiormente ( inferiormente ) se traduce en que existe una linea horizontal (
paralela al eje
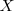 ), tal que ningun punto de la grafica se encuentra por encima ( debajo ) de dicha recta.
), tal que ningun punto de la grafica se encuentra por encima ( debajo ) de dicha recta.
Propiedad 2
Una función
 con una asintota vertical
no puede estar acotada, pero puede estar acotada superior o inferiormente.
con una asintota vertical
no puede estar acotada, pero puede estar acotada superior o inferiormente.
Mas concretamente:
- Si existe un número real
 ,
tal que
,
tal que
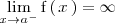 o
o
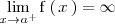 , entonces
, entonces
 no esta acotada superiormente.
no esta acotada superiormente.
- Reciprocamente, si existe un número real
 ,
tal que
,
tal que
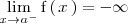 o
o
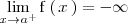 , entonces
, entonces
 no esta acotada inferiormente.
no esta acotada inferiormente.
Propiedad 3
Si
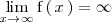 o
o
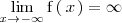 ,
entonces
,
entonces
 NO esta acotada superiormente.
NO esta acotada superiormente.
Si
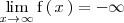 o
o
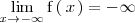 ,
entonces
,
entonces
 NO esta acotada inferiormente.
NO esta acotada inferiormente.
Ejemplo
La función
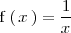
tiene una asintota vertical de ecuación
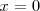 .
Por lo tanto, la función
.
Por lo tanto, la función
 no esta acotada.
no esta acotada.
Para averiguar si esta acotada superior o inferiormente, calculamos cada uno de los siguientes limites laterales:
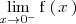
y
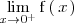
El primero es
 y el segundo es
y el segundo es
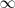 .
Por lo tanto,
.
Por lo tanto,
 no esta acotada ni superior, ni inferiormente.
no esta acotada ni superior, ni inferiormente.
Ejemplo
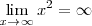
Por lo tanto,
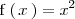 no esta acotada superiormente.
no esta acotada superiormente.



