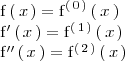Navegación
Herramientas
Función derivada y derivadas sucesivas
De Wikillerato
(Diferencias entre revisiones)
| Línea 96: | Línea 96: | ||
<br/> | <br/> | ||
| - | + | Así | |
<center> | <center> | ||
<math> | <math> | ||
\begin{array}{l} | \begin{array}{l} | ||
| - | \mathrm{f} = \mathrm{f}^{\left( \, 0 \, \right)} | + | \mathrm{f} \left( \, x \, \right) = \mathrm{f}^{\left( \, 0 \, \right)} \left( |
| + | \, x \, \right) | ||
\\ | \\ | ||
| - | \mathrm{f}^\prime = \mathrm{f}^{\left( \, 1 \, \right)} | + | \mathrm{f}^\prime \left( \, x \, \right) = \mathrm{f}^{\left( \, 1 \, \right)} |
| + | \left( \, x \, \right) | ||
\\ | \\ | ||
| - | \mathrm{f}^{\prime\prime} = \mathrm{f}^{\left( \, 2 \, \right)} | + | \mathrm{f}^{\prime\prime} \left( \, x \, \right) = \mathrm{f}^{\left( \, 2 \, |
| - | \end{array} | + | \right)} \left( \, x \, \right) |
| + | \end{array} | ||
</math> | </math> | ||
</center> | </center> | ||
Revisión actual
Una función
es derivable en el intervalo
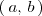si lo es en cada punto de dicho intervalo.
Si
es una función derivable en el intervalo
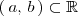, la función derivada de
es la que a cada
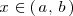le hace corresponder la derivada de
en dicho punto. Esta función se designa por
.
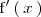Llamamos derivada de segundo orden o derivada segunda de
a la función derivada de
.
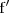Esta función se denota por
.
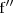Llamamos derivada de tercer orden o derivada tercera de
a la función derivada de
.
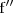Esta función se denota por
.
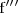En general, llamamos
derivada n-ésima de
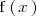y la denotamos por
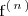a la función derivada de
.
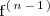Así
Tweet
