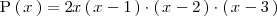Procedimiento para factorizar un polinomio
De Wikillerato
| Línea 1: | Línea 1: | ||
| + | |||
<br/> | <br/> | ||
| Línea 115: | Línea 116: | ||
es un divisor de | es un divisor de | ||
<math> | <math> | ||
| - | + | a_0 | |
</math>, | </math>, | ||
utilizando para ello la [[Regla de Ruffini|regla de Ruffini]] | utilizando para ello la [[Regla de Ruffini|regla de Ruffini]] | ||
| Línea 193: | Línea 194: | ||
Como se trata de un polinomio de grado mayor que dos y con coeficiente enteros, | Como se trata de un polinomio de grado mayor que dos y con coeficiente enteros, | ||
utilizamos la [[Regla de Ruffini|regla de Ruffini]] con este polinomio y con | utilizamos la [[Regla de Ruffini|regla de Ruffini]] con este polinomio y con | ||
| - | + | las fracciones de la forma | |
<math> | <math> | ||
| - | \frac{ | + | \frac{a}{b} |
| - | </math> | + | </math>, |
| - | + | donde | |
<math> | <math> | ||
| - | + | a | |
</math> | </math> | ||
| - | </ | + | es un divisor de |
| - | + | <math> | |
| + | a_0 = -12 | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | b | ||
| + | </math> | ||
| + | es un divisor de | ||
| + | <math> | ||
| + | a_3 = 2 | ||
| + | </math>. | ||
| + | | ||
| + | Utilizando la regla de Ruffini con estas fracciones encontramos que 3 es una raiz de | ||
<math> | <math> | ||
\mathrm{Q} \left( \, x \, \right) | \mathrm{Q} \left( \, x \, \right) | ||
Revisión de 15:41 9 feb 2011
1.
Sacamos  factor común, si ello es posible, y tantas veces
como se pueda.
factor común, si ello es posible, y tantas veces
como se pueda.
2.
Si el polinomio
 es de grado dos:
es de grado dos:
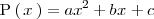
resolvemos la ecuación
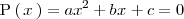
Si esta ecuación no tiene solución, el polinomio
 es irreducible,
pero si la ecuación anterior tiene soluciones
es irreducible,
pero si la ecuación anterior tiene soluciones
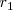 y
y
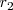 ,
entonces podemos factorizar
,
entonces podemos factorizar
 de la siguiente manera:
de la siguiente manera:
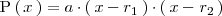
Puede ocurrir que
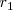 y
y
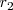 coincidan ( sean iguales ).
coincidan ( sean iguales ).
3. Si el polinomio
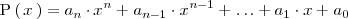
• es de grado mayor que dos y
• sus coeficientes son enteros,
intentamos encontrar las raices reales del polinomio
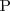 entre los números racionales de la forma
entre los números racionales de la forma
 donde
donde
 es un divisor de
es un divisor de
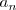 y
y
 es un divisor de
es un divisor de
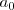 ,
utilizando para ello la regla de Ruffini
con cada una de estas fracciones y con el polinomio
,
utilizando para ello la regla de Ruffini
con cada una de estas fracciones y con el polinomio
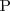 .
.
si y solo si
es divisor de
.
Así, si llegado a un cierto punto en el proceso de factorización hemos encontrado raices
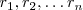 del polinomio
del polinomio
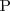 ,
entonces existe un polinomio
,
entonces existe un polinomio
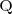 tal que
tal que
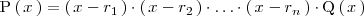
e intentariamos descomponer mas
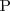 factorizando
factorizando
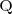 .
.
Ejemplo
Factorizemos el polinomio:
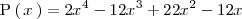
Como se puede sacar un
 factor común, eso es lo primero que hacemos:
factor común, eso es lo primero que hacemos:
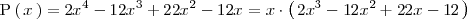
A continuación factorizamos
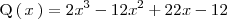
Como se trata de un polinomio de grado mayor que dos y con coeficiente enteros,
utilizamos la regla de Ruffini con este polinomio y con
las fracciones de la forma
 ,
,
donde
 es un divisor de
es un divisor de
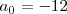 y
y
 es un divisor de
es un divisor de
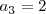 .
Utilizando la regla de Ruffini con estas fracciones encontramos que 3 es una raiz de
.
Utilizando la regla de Ruffini con estas fracciones encontramos que 3 es una raiz de
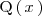 ,
es decir,
,
es decir,
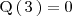 ,
y que
,
y que
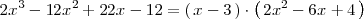
Finalmente, factorizamos el polinomio
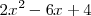
resolviendo la ecuación
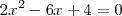
cuyas soluciones son 2 y 1, de manera que
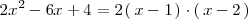
y, por tanto