Teorema de Bayes
De Wikillerato
| Línea 9: | Línea 9: | ||
A_1, \, A_2, \, \ldots, \, A_n \, | A_1, \, A_2, \, \ldots, \, A_n \, | ||
</math> | </math> | ||
| - | sucesos incompatibles dos a dos, tales que siempre ocurre alguno de ellos | + | sucesos incompatibles dos a dos, tales que siempre ocurre alguno de ellos, y sea |
| - | + | ||
<math> | <math> | ||
B | B | ||
| Línea 60: | Línea 59: | ||
\cdot \mathrm{P} | \cdot \mathrm{P} | ||
\left( | \left( | ||
| - | \, B \, \left| \, A_1 \, \right | + | \, B \, \left| \, A_1 \, \right) |
\right) | \right) | ||
\, + \, | \, + \, | ||
| Línea 69: | Línea 68: | ||
\cdot \mathrm{P} | \cdot \mathrm{P} | ||
\left( | \left( | ||
| - | \, B \, \left| \, A_2 \, \right | + | \, B \, \left| \, A_2 \, \right) |
\, + \, \ldots \, + \, | \, + \, \ldots \, + \, | ||
\mathrm{P} | \mathrm{P} | ||
| Línea 77: | Línea 76: | ||
\cdot \mathrm{P} | \cdot \mathrm{P} | ||
\left( | \left( | ||
| - | \, B \, \left| \, A_n \, \right | + | \, B \, \left| \, A_n \, \right) |
\right) | \right) | ||
} | } | ||
| Línea 282: | Línea 281: | ||
\left( | \left( | ||
\, R \, \left| \, U_2 \, \right. | \, R \, \left| \, U_2 \, \right. | ||
| + | \right) | ||
\, + \, | \, + \, | ||
\mathrm{P} | \mathrm{P} | ||
Revisión de 19:27 26 dic 2006
Tabla de contenidos[ocultar] |
Enunciado
Sean
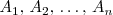 sucesos incompatibles dos a dos, tales que siempre ocurre alguno de ellos, y sea
sucesos incompatibles dos a dos, tales que siempre ocurre alguno de ellos, y sea
 un suceso cualquiera del que se conocen las probabilidades condicionales
un suceso cualquiera del que se conocen las probabilidades condicionales
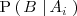 .
.
Entonces las probabilidades
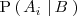 vienen dadas por la expresión:
vienen dadas por la expresión:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Demostración
Por definición de probabilidad condicionada
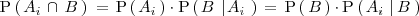
despejando [Unparseable or potentially dangerous latex formula. Error 3 ] , se tiene:
[Unparseable or potentially dangerous latex formula. Error 3 ]
La probabilidad
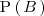 , por el teorema de la probabilidad total, es igual a
, por el teorema de la probabilidad total, es igual a
[Unparseable or potentially dangerous latex formula. Error 3 ]
Sustituyendo en la ecuación anterior, obtenemos la fórmula de Bayes.
Ejemplo
Tenemos tres urna:
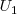 con tres bolas rojas y 5 negras,
con tres bolas rojas y 5 negras,
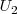 con dos bolas rojas y una negra y
con dos bolas rojas y una negra y
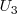 con dos bolas rojas y tres negras. Escogemos una urna al azar y extraemos una
bola. Si la bola ha sido roja, ¿cuál es la probabilidad de haber sido extraída de la urna
con dos bolas rojas y tres negras. Escogemos una urna al azar y extraemos una
bola. Si la bola ha sido roja, ¿cuál es la probabilidad de haber sido extraída de la urna
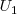 ?
?
Llamamos
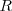 al suceso sacar bola roja. La probabilidad pedida es
al suceso sacar bola roja. La probabilidad pedida es
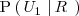 . Utilizando el teorema de Bayes, tenemos:
. Utilizando el teorema de Bayes, tenemos:
[Unparseable or potentially dangerous latex formula. Error 3 ]



