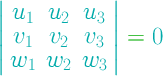Dependencia e independencia lineal
De Wikillerato
Una combinación lineal de los vectores
 , es una suma de la forma:
, es una suma de la forma:
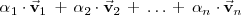
siendo los coeficientes
 numeros reales.
numeros reales.
Ejemplo:
Dados los vectores
 y
y
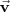 , una combinación lineal de ellos es el vector
, una combinación lineal de ellos es el vector
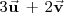
Los vectores
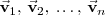 son linealmente independientes si:
son linealmente independientes si:
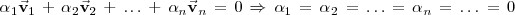
Ejemplo:
Los vectores
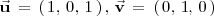 y
y
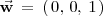 son linealmente independientes, pues:
son linealmente independientes, pues:

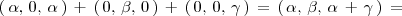
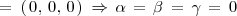
Los vectores
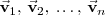 son linealmente independientes si existen escalares
son linealmente independientes si existen escalares
 no todos nulos tales que:
no todos nulos tales que:
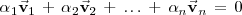
Ejemplo:
Los vectores
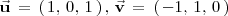 y
y
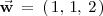 son linealmente dependientes, pues:
son linealmente dependientes, pues:

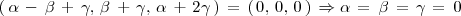
Igualando componentes:
![\left.
</p>
<pre> \begin{array}[c]{rcl}
\alpha\, - \, \beta \, + \, \gamma & = & 0
\\
\beta \, + \, \gamma & = & 0
\\
\alpha \, + \, 2\gamma & = & 0
\end{array}
</pre>
<p>\right\}
</p>
<pre>\, \Rightarrow \beta \, = \, -\gamma, \, \alpha \, = \, -2\gamma
</pre>
<p>
\left.
</p>
<pre> \begin{array}[c]{rcl}
\alpha\, - \, \beta \, + \, \gamma & = & 0
\\
\beta \, + \, \gamma & = & 0
\\
\alpha \, + \, 2\gamma & = & 0
\end{array}
</pre>
<p>\right\}
</p>
<pre>\, \Rightarrow \beta \, = \, -\gamma, \, \alpha \, = \, -2\gamma
</pre>
<p>](/images/math/math-5df83e3ec529fee5da2501449dc541a7.png)
Para cualquier valor que tome
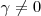 se obtiene un valor para
se obtiene un valor para
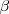 y otro para
y otro para
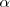 tambien distintos de cero, luego
tambien distintos de cero, luego
 ,
,
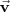 y
y
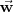 son linealmente dependientes.
son linealmente dependientes.
En
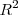 , dos vectores
, dos vectores
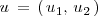 y
y
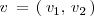 son:
son:
|
linealmente independientes si: |
linealmente dependientes si: |
|---|---|
|
|
|
En
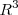 , tres vectores
, tres vectores
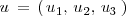 ,
,
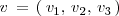 y
y
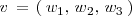 son:
son:
|
linealmente independientes si: |
linealmente dependientes si: |
|---|---|
|
|
|