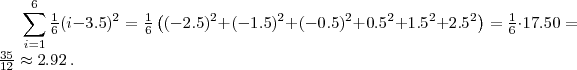Navegación
Varianza
De Wikillerato
La varianza de una variable aleatoria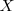 
es una medida de su dispersión. Sea ![\mu = E[x]](/images/math/math-7e23466124d060bd3e431b9e70905233.png "\mu = E[x]")
, la definición formal de la varianza es:
![Var[X] = \sigma^{2}(X) = E[(X- \mu)^2]](/images/math/math-acc22b304d7b2be938e215397f12e0ec.png "Var[X] = \sigma^{2}(X) = E[(X- \mu)^2]")
Existe una formalización alternativa que en muchos casos puede facilitar los cálculos. Esta se deriva desde esta primera de la siguiente manera:
![Var(X) & = E[ ( X - \mu ) ^ 2 ] \\
& = E[ ( X ^ 2 - 2X\mu + \mu ^ 2) ] \\
& = E( X ^ 2) - 2\mu E(X) + \mu ^ 2 \\
& = E( X ^ 2) - 2\mu ^ 2 + \mu ^ 2 \\
& = {E} ( X ^ 2) - \mu ^ 2](/images/math/math-c6f30a94580d32a8676f80aa79913135.png "Var(X) & = E[ ( X - \mu ) ^ 2 ] \\
& = E[ ( X ^ 2 - 2X\mu + \mu ^ 2) ] \\
& = E( X ^ 2) - 2\mu E(X) + \mu ^ 2 \\
& = E( X ^ 2) - 2\mu ^ 2 + \mu ^ 2 \\
& = {E} ( X ^ 2) - \mu ^ 2")
Caso discreto
En caso que 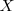sea una variable aleatoria discreta con valores 
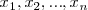y sus probabilidades estén representadas por la función de probabilidad 
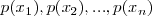, la se calcula como:
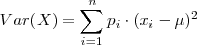
donde
.
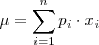Caso continuo
Si la variable aleatoria 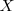es una variable aleatoria continua con función de densidad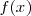 
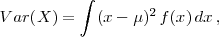
donde
![\mu = \int x \, f(x) \, dx\ = E[X]](/images/math/math-51fcaaaef62d29bffc52945f48170b59.png "\mu = \int x \, f(x) \, dx\ = E[X]")
y las integrales están definidas sobre el rango de .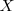
Propiedades de la varianza
Algunas propiedades de la varianza son:
-
-
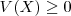
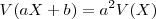siendo a y b números reales cualesquiera. De esta propiedad se deduce que la varianza de una constante es cero, es decir,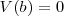 
-
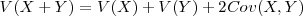, donde Cov(X,Y) es la covarianza de X e Y.
-
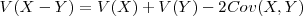, donde Cov(X,Y) es la covarianza de X e Y.
Ejemplo
Dado perfecto
Un dado de seis caras puede representarse como una variable aleatoria discreta que toma, valores del 1 al 6 con probabilidad igual a 1/6. El valor esperado es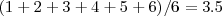 
. Por lo tanto, su varianza es:
