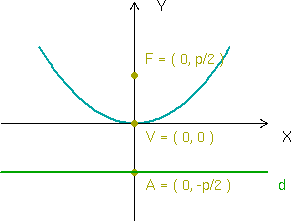Parábola
De Wikillerato
Tabla de contenidos[ocultar] |
Definición
Llamamos lugar geometrico al conjunto de puntos que satisfacen una determinada propiedad.
Llamamos parábola al lugar geométrico de los puntos de un plano que equidistan
de un punto fijo
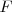 y de una recta fija
y de una recta fija
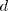 .
.
Veamos cuales son los elementos de la parábola:
1. El punto
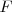 se denomina foco y la recta
se denomina foco y la recta
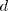 es la directriz de la parábola.
es la directriz de la parábola.
2. La recta que pasa por el foco y es perpendicular a la directriz se llama eje de la parábola. En la figura de arriba el eje de la parábola coincide con el eje
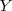 .
.
3. El punto en el que el eje corta a la parábola recibe el nombre de vértice.
(
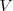 en la figura de arriba )
en la figura de arriba )
4. Se denomina parámetro,
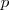 , a la distancia del foco a la directriz.
, a la distancia del foco a la directriz.
Ecuación
La condición:
"los puntos de la parábola equidistan de
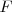 y de
y de
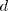 ."
."
se puede expresar matematicamente de la siguiente forma:
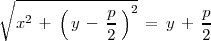
donde el miembro de la izquierda es la distancia de un punto
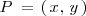 a
a
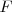 y el miembro de la derecha es la distancia de
y el miembro de la derecha es la distancia de
 a
a
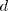 .
.
Elevando al cuadrado y agrupando terminos semejantes, obtenemos:
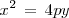
Así, podemos generalizar esta ecuación para parábolas no solo verticales sino también horizontales y cuyo vertice no se encuentre en el origen (0,0).
La ecuación para una parábola vertical es
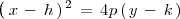
Esta parábola tiene su vertice en el punto (h,k) y es concava hacia arriba si p>0 y es hacia abajo si p<0.
Para obtener la ecuación de una parabola horizontal, como es de esperarse, se intercambian en la ecuación anterior los lugares de "x" y de "y". Es como si giraramos el plano cartesiano 90º. De esta forma la parabola abre hacia la derecha si p>0 y hacia la izquierda si p<0.
Ejemplo
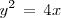
es la ecuación de una parábola cuyo eje es el eje
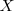 y cuya directriz es la recta de ecuación:
y cuya directriz es la recta de ecuación:
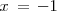 . Su foco es el punto
. Su foco es el punto
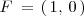 .
.
Referencias
- Cónicas: Ecuaciones de la hipérbola y la parábola, Pilar Ferrero Casado. Matemáticas: ESO, Bachillerato y Selectividad.