Continuidad de una función en un punto
De Wikillerato
(Diferencias entre revisiones)
(→Texto de titular) |
(→Referencias) |
||
| (3 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | Una función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | es continua en el punto | ||
| + | <math> | ||
| + | x \, = \, x_0 | ||
| + | </math> | ||
| + | si | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) \, = \, | ||
| + | \mathrm{f} \left( \, x_0 \, \right) | ||
| + | </math>. | ||
| - | = | + | <br/> |
| - | <math> | + | |
| + | El que una función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | sea continua en el punto | ||
| + | <math> | ||
| + | x \, = \, x_0 | ||
| + | </math> | ||
| + | implica que | ||
| + | <math> | ||
| + | \mathrm{f} \left( \, x_0 \, \right) | ||
| + | </math> | ||
| + | existe y que | ||
| + | <math> | ||
| + | \lim_{x \to x_0} \mathrm{f} \left( \, x \, \right) | ||
| + | </math> | ||
| + | tambien existe. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Una función es continua en un intervalo si es continua en todos los puntos del intervalo. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Una fución es continua en todo su dominio cuando lo es en todos los puntos que lo | ||
| + | componen. | ||
| + | |||
| + | |||
| + | == Referencias == | ||
| + | # ''[http://www.vadenumeros.es/primero/tipos-de-discontinuidad.htm Continuidad de una función en un punto]'', Pilar Ferrero Casado. Matemáticas: ESO, Bachillerato y Selectividad | ||
| + | |||
| + | [[Category:Matemáticas]] | ||
Revisión actual
Una función
 es continua en el punto
es continua en el punto
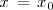 si
si
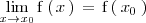 .
.
El que una función
 sea continua en el punto
sea continua en el punto
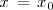 implica que
implica que
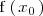 existe y que
existe y que
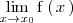 tambien existe.
tambien existe.
Una función es continua en un intervalo si es continua en todos los puntos del intervalo.
Una fución es continua en todo su dominio cuando lo es en todos los puntos que lo componen.
Referencias
- Continuidad de una función en un punto, Pilar Ferrero Casado. Matemáticas: ESO, Bachillerato y Selectividad



