Radiación del Cuerpo Negro. Hipótesis de Planck
De Wikillerato
| (6 ediciones intermedias no se muestran.) | |||
| Línea 28: | Línea 28: | ||
donde T es la temperatura absoluta en grados Kelvin, <math>k = 5.6703 x 10^{-8} W/m^2K^4</math> (en unidades de [[Sistema Internacional de Medidas]]: W, vatios; m metros, K, grados Kelvin) es una constante llamada de '''constante de Stefan-Bolztmann'''. Este resultado fue también derivado a través de consideraciones teóricas con base en la termodinámica clásica por un alumno de Stefan, el físico austriaco Ludwing Boltzmann (1844-1906) cinco años más tarde en 1884, por lo que la ecuación <math>[1]</math> es llamada '''ley de Stefan-Boltzmann'''. Esta ecuación nos indica que la cantidad total de energía radiada (la''' emitancia total o poder emisivo total''') por un cuerpo negro en equilibrio térmico aumenta con la cuarta potencia de su temperatura absoluta. | donde T es la temperatura absoluta en grados Kelvin, <math>k = 5.6703 x 10^{-8} W/m^2K^4</math> (en unidades de [[Sistema Internacional de Medidas]]: W, vatios; m metros, K, grados Kelvin) es una constante llamada de '''constante de Stefan-Bolztmann'''. Este resultado fue también derivado a través de consideraciones teóricas con base en la termodinámica clásica por un alumno de Stefan, el físico austriaco Ludwing Boltzmann (1844-1906) cinco años más tarde en 1884, por lo que la ecuación <math>[1]</math> es llamada '''ley de Stefan-Boltzmann'''. Esta ecuación nos indica que la cantidad total de energía radiada (la''' emitancia total o poder emisivo total''') por un cuerpo negro en equilibrio térmico aumenta con la cuarta potencia de su temperatura absoluta. | ||
| - | Los objetos que no son cuerpos negros radian energía por unidad de área a una tasa menor que la del cuerpo negro a la misma temperatura. Esa tasa dependen en otras propiedades además de la temperatura, tales como el color y la composición de la superficie. El efecto de estas dependencias es combinado en en un facto llamado''' emisividad''' <math>\ | + | Los objetos que no son cuerpos negros radian energía por unidad de área a una tasa menor que la del cuerpo negro a la misma temperatura. Esa tasa dependen en otras propiedades además de la temperatura, tales como el color y la composición de la superficie. El efecto de estas dependencias es combinado en en un facto llamado''' emisividad''' <math>\epsilon</math> el cual debe ser incluido como factor multiplicador en la ecuación <math>[1]</math>. El valor de <math>\epsilon</math>es también dependiente de la temperatura y siempre es menor que la unidad. |
La distribución espectral de la radiación emitida por un cuerpo negro se encuentra que es empíricamente dependiente de la temperatura absoluta, mientras que la forma de la curva de emisión es independiente de la forma de la cavidad, como también, de la naturaleza del material de las paredes. | La distribución espectral de la radiación emitida por un cuerpo negro se encuentra que es empíricamente dependiente de la temperatura absoluta, mientras que la forma de la curva de emisión es independiente de la forma de la cavidad, como también, de la naturaleza del material de las paredes. | ||
| - | Al igual que el poder radiado total <math>R</math>, la '''distribución espectral''' de la radiación emitida por un cuerpo negro se encuentra empíricamente que depende de la temperatura absoluta T. Si se representa para una determinada temperatura gráficamente el poder emitido por unidad de área <math>R</math>, en función de longitud de onda (<math>\lambda</math>) la llamada ''función de distribución espectral'' <math> R(\lambda,T)</math> (la notación matemática expresa que la función <math>R</math> depende de las dos variables, <math>\lambda</math> y T), se obtiene un curva acampanada lisa que tiende a cero tanto para longitudes de onda muy larga, como para longitudes de onda muy corta, en general la curva presenta un máximo para cierta longitud de onda <math>\lambda^max</math> que depende de la temperatura absoluta T de manera muy simple: | + | Al igual que el poder radiado total <math>R</math>, la '''distribución espectral''' de la radiación emitida por un cuerpo negro se encuentra empíricamente que depende de la temperatura absoluta T. Si se representa para una determinada temperatura gráficamente el poder emitido por unidad de área <math>R</math>, en función de longitud de onda (<math>\lambda</math>) la llamada ''función de distribución espectral'' <math> R(\lambda,T)</math> (la notación matemática expresa que la función <math>R</math> depende de las dos variables, <math>\lambda</math> y T), se obtiene un curva acampanada lisa que tiende a cero tanto para longitudes de onda muy larga, como para longitudes de onda muy corta, en general la curva presenta un máximo para cierta longitud de onda <math>\lambda^{max}</math> que depende de la temperatura absoluta T de manera muy simple: |
| - | <math>\lambda^{max}T = Constante [Co]=2.898x10^{-3} m K</math> <math>[2]</math> | + | <math>\lambda^{max}T = Constante [Co]=2.898x10^{-3} m . K</math> <math>[2]</math> |
| - | Este resultado expresa '''la ley de desplazamiento de Wien''' | + | Este resultado expresa '''la ley de desplazamiento de Wien''' que fue obtenida por el físico alemán Wilhelm Wien (1864-1928). Desplazamiento en referencia al desplazamiento hacia longitudes de onda más corta que sufre el máximo de la curva conforme se incrementa la temperatura. Así, la longitud en la cual la distribución (emisión) es máxima varia inversamente con la temperatura. La constante <math>Co</math> es una [[constante universal]] que describe una propiedad de las cavidades o superficies radiantes en general. La cantidad total de radiación emitida es más o menos la misma para todas las superficies materiales. |
El poder radiado fuera del agujero <math>R</math> es proporcional a la ''densidad total de energía'' <math>\rho</math>(energía por unidad de volumen de la radiación en la cavidad del cuerpo negro ideal). Se puede demostrar que la [[constante de proporcionalidad]] es igual <math>c/4</math> donde <math>c</math> es la velocidad de la luz. | El poder radiado fuera del agujero <math>R</math> es proporcional a la ''densidad total de energía'' <math>\rho</math>(energía por unidad de volumen de la radiación en la cavidad del cuerpo negro ideal). Se puede demostrar que la [[constante de proporcionalidad]] es igual <math>c/4</math> donde <math>c</math> es la velocidad de la luz. | ||
| Línea 46: | Línea 46: | ||
<math>R(\lambda,T)=1/4c\rho(\lambda,T)</math> <math>[4]</math> | <math>R(\lambda,T)=1/4c\rho(\lambda,T)</math> <math>[4]</math> | ||
| - | Esta relación se cumple para para cualquier cuerpo negro en equilibrio térmico. ''La función de distribución de densidad de energía'' <math>\rho(\lambda,T)</math> en el interior de la cavidad del cuerpo negro es completamente independiente de las propiedades y formas de los cuerpos puede que forma la pared del recinto del cuerpo negro. Por ello el espectro de radiación térmica emitido por un cuerpo negro en equilibrio térmico posee características universales. Una universalidad que cumple con el [[segundo principio de la termodinámica]]. Las funciones son por tanto ''funciones universales'' dependientes únicamente de la longitud de onda (o de la frecuencia ) y de la temperatura absoluta <math>\rho(\lambda,T)</math> y <math> R(\lambda,T)</math> | + | Esta relación se cumple para para cualquier cuerpo negro en equilibrio térmico. ''La función de distribución de densidad de energía'' <math>\rho(\lambda,T)</math> en el interior de la cavidad del cuerpo negro es completamente independiente de las propiedades y formas de los cuerpos puede que forma la pared del recinto del cuerpo negro. Por ello el espectro de radiación térmica emitido por un cuerpo negro en equilibrio térmico posee características universales. Una universalidad que cumple con el [[segundo principio de la termodinámica]]. Las funciones son por tanto ''funciones universales'' dependientes únicamente de la longitud de onda (o de la frecuencia ) y de la temperatura absoluta <math>\rho(\lambda,T)</math> y <math> R(\lambda,T)</math>. |
La función <math> \rho(\lambda,T)</math> puede ser calculada a partir de la física clásica de manera sencilla. El método requiere encontrar el número de modos de oscilación del campo electromagnético en la cavidad con la longitud de onda en la cavidad en el intervalo <math>\lambda</math> y multiplicando la energía promedio por nodo. El resultado es que el número de modos de oscilación por unidad de volumen n(<math>\lambda</math>) es independiente de la forma de la cavidad elegida y es dado por <math>n(\lambda)=8 \pi \lambda^{-4}</math> <math>[5]</math>. De acuerdo con la [[teoría cinética clásica]] la energía promedio por modo de oscilación es <math>kT</math>, la misma que para un oscilador armónico en una dimensión, <math>k</math> es la '''constante de Boltzmann''' <math> k =1.3806503 x 10^{- 23} J/K </math>. | La función <math> \rho(\lambda,T)</math> puede ser calculada a partir de la física clásica de manera sencilla. El método requiere encontrar el número de modos de oscilación del campo electromagnético en la cavidad con la longitud de onda en la cavidad en el intervalo <math>\lambda</math> y multiplicando la energía promedio por nodo. El resultado es que el número de modos de oscilación por unidad de volumen n(<math>\lambda</math>) es independiente de la forma de la cavidad elegida y es dado por <math>n(\lambda)=8 \pi \lambda^{-4}</math> <math>[5]</math>. De acuerdo con la [[teoría cinética clásica]] la energía promedio por modo de oscilación es <math>kT</math>, la misma que para un oscilador armónico en una dimensión, <math>k</math> es la '''constante de Boltzmann''' <math> k =1.3806503 x 10^{- 23} J/K </math>. | ||
| Línea 56: | Línea 56: | ||
Utilizando argumentos de electrodinámica clásica el físico inglés John-Willian Struct (Lord Rayleigh) (1842-1919) derivó y posteriormente fue modificada por sir James James (1877-1946) una función teórica de distribución espectral de densidad de energía <math>\rho(\lambda,T)</math>: | Utilizando argumentos de electrodinámica clásica el físico inglés John-Willian Struct (Lord Rayleigh) (1842-1919) derivó y posteriormente fue modificada por sir James James (1877-1946) una función teórica de distribución espectral de densidad de energía <math>\rho(\lambda,T)</math>: | ||
| - | <math>\rho(\lambda,T)=8\pi kT/\lambda^{4}</math> <math>[6]</math>; en función de la frecuencia <math>\rho(\nu, T)=8\ | + | <math>\rho(\lambda,T)=8\pi kT/\lambda^{4}</math> <math>[6]</math>; en función de la frecuencia <math>\rho(\nu, T)=\frac{8\pi kT\nu^{2}}{c^3}</math> <math>[7]</math>, llamada '''ley de Rayleigh-Jeans''', donde <math>k</math> es la constante de Boltzmann. |
Esta ley muestra un serio conflicto entre las predicciones de la física clásica y los resultados experimentales. A muy bajas longitudes de onda esta ley estaba de acuerdo con la distribución espectral determinada experimentalmente, pero a longitudes de ondas corta de más alta frecuencia esta ley predice que <math>\rho(\lambda,T)</math> va incrementando de valor aproximándose a la infinidad cuando <math>\lambda->0</math>, mientras que experimentalmente se comprueba que la distribución se aproxima cero cuando<math>\lambda->0</math>. Este enorme desacuerdo entre la mediada experimental de <math>(\lambda,T)</math> y la predicción fundamental de la física clásica a longitudes de onda corta fue llamada en 1911 por el físico austriaco, uno de los padres de la [[Teoría cuántica]] Paul S. Ehrenfest (1880-1933) ''la catástrofe ultravioleta'', la ley de radiación Rayleigh-Jeans predecía una gran emisión de radiación ultravioleta UV por el cuerpo negro, cosa que experimentalmente no ocurre . Este ''comportamiento anómalo'' indicaría por ejemplo que seríamos abrasados por cualquier horno o pedazo de hierro incandescente , lo cual evidentemente no ocurre. O en palabras del físico y divulgador científico de origen ucraniano conocido con el nombre de George Gamov (1904-1968), “...al abrir la puerta del horno de una cocina o el cierre del hogar de una locomotora, seriamos alcanzado por la mortal radiación de las ondas cortas y moriríamos inmediatamente. La conclusión es evidentemente absurda , pero por otra parte resulta de la aplicación de las leyes fundamentales de la física clásica a la energía radiante. | Esta ley muestra un serio conflicto entre las predicciones de la física clásica y los resultados experimentales. A muy bajas longitudes de onda esta ley estaba de acuerdo con la distribución espectral determinada experimentalmente, pero a longitudes de ondas corta de más alta frecuencia esta ley predice que <math>\rho(\lambda,T)</math> va incrementando de valor aproximándose a la infinidad cuando <math>\lambda->0</math>, mientras que experimentalmente se comprueba que la distribución se aproxima cero cuando<math>\lambda->0</math>. Este enorme desacuerdo entre la mediada experimental de <math>(\lambda,T)</math> y la predicción fundamental de la física clásica a longitudes de onda corta fue llamada en 1911 por el físico austriaco, uno de los padres de la [[Teoría cuántica]] Paul S. Ehrenfest (1880-1933) ''la catástrofe ultravioleta'', la ley de radiación Rayleigh-Jeans predecía una gran emisión de radiación ultravioleta UV por el cuerpo negro, cosa que experimentalmente no ocurre . Este ''comportamiento anómalo'' indicaría por ejemplo que seríamos abrasados por cualquier horno o pedazo de hierro incandescente , lo cual evidentemente no ocurre. O en palabras del físico y divulgador científico de origen ucraniano conocido con el nombre de George Gamov (1904-1968), “...al abrir la puerta del horno de una cocina o el cierre del hogar de una locomotora, seriamos alcanzado por la mortal radiación de las ondas cortas y moriríamos inmediatamente. La conclusión es evidentemente absurda , pero por otra parte resulta de la aplicación de las leyes fundamentales de la física clásica a la energía radiante. | ||
| Línea 64: | Línea 64: | ||
<h4>Planck y el inicio de la Revolución Cuántica</h4> | <h4>Planck y el inicio de la Revolución Cuántica</h4> | ||
| - | El catorce de diciembre del año 1900 en los albores del siglo XX, el físico alemán Max Planck (1858-1947) presentó un trabajo acerca de la ley de la radiación del cuerpo negro en una reunión de la Sociedad Alemana de Física, en Berlin, y esta fecha puede considerarse como el nacimiento de la física cuántica. En su deducción de la expresión teórica de la intensidad de radiación en función de la longitud de onda y de la temperatura, Planck abandonó la física clásica al introducir un hipótesis radical ''ad hoc'' cuya esencia puede formularse como sigue | + | El catorce de diciembre del año 1900 en los albores del siglo XX, el físico alemán Max Planck (1858-1947) presentó un trabajo acerca de la ley de la radiación del cuerpo negro en una reunión de la Sociedad Alemana de Física, en Berlin, y esta fecha puede considerarse como el nacimiento de la física cuántica. En su deducción de la expresión teórica de la intensidad de radiación en función de la longitud de onda y de la temperatura, Planck abandonó la física clásica al introducir un hipótesis radical ''ad hoc'' cuya esencia puede formularse como sigue: Un oscilador de frecuencia natural <math>\nu</math> puede'' tomar o ceder energía'' únicamente en proporciones de magnitud <math>E=h\nu</math> <math>[8]</math>, donde <math>h</math> es una nueva constante de la naturaleza, llamada en honor de Planck '''constante de Planck''' (el ''cuanto de acción'', pues tiene [[dimensiones de acción]] (energía por tiempo) J.s; Julios (J), unidad de energía por segundo (s) unidad de tiempo) y solo puede tener, y por lo tanto solo emitir energía dadas por <math>E=nh\nu</math><math>[9]</math>, donde <math>n</math> es un entero positivo, <math>\nu</math> la frecuencia de la radiación. Planck fue capaz con esta hipótesis encontrar una expresión teórica para la función de distribución espectral de densidad energía en función de la longitud de onda <math>(\lambda, T) </math>o de la frecuencia <math>(\rho, T) </math>de la radiación de la cavidad del cuerpo negro: |
<math>\rho(\lambda,T) =\frac{8\pi hc} {\lambda^{5}}\frac{1}{ e^{\frac{hc}{\lambda kT}}-1}</math> <math>[10]</math> | <math>\rho(\lambda,T) =\frac{8\pi hc} {\lambda^{5}}\frac{1}{ e^{\frac{hc}{\lambda kT}}-1}</math> <math>[10]</math> | ||
| - | <math>\rho(\nu,T) =\frac{ | + | <math>\rho(\nu,T) =\frac{8\pi\nu^{2}}{c^3}\frac{h\nu}{ e^{\frac{h\nu}{kT}}-1}</math> <math>[11]</math> |
| - | Donde <math> \rho(\lambda,T)</math> es la densidad de energía radiante en la cavidad por unidad de intervalo de longitud de onda, para la longitud de onda <math>\lambda</math>, | + | Donde <math> \rho(\lambda,T)</math> es la densidad de energía radiante en la cavidad por unidad de intervalo de longitud de onda, para la longitud de onda <math>\lambda</math>, a la tempera absoluta <math>T</math>, la constante <math>k</math> es la constante de Boltzmann, y <math>c</math> es la velocidad de la luz, y <math>h</math> es la '''constante de Planck'''. |
| - | Esta función llamada '''ley de Planck''' se ajustaba muy bien a los datos obtenidos experimentalmente. El valor de la constante de Planck <math>h</math>, puede ser determinado encajando la función de la ecuación a los datos experimentales. El valor actual aceptado para la constante <math | + | Esta función llamada '''ley de Planck''' se ajustaba muy bien a los datos obtenidos experimentalmente. El valor de la constante de Planck <math>h</math>, puede ser determinado encajando la función de la ecuación a los datos experimentales. El valor actual aceptado para la constante <math>h</math> es igual: |
<math>h= 6.626 x10^{-34} J.s = 4.136 x10^{-15} eV.s</math> | <math>h= 6.626 x10^{-34} J.s = 4.136 x10^{-15} eV.s</math> | ||
Revisión actual
Tabla de contenidos |
Radiación del Cuerpo Negro. Hipótesis de Planck
Antecedentes históricos
Es bien conocida la anécdota de que a finales del siglo XIX un destacado físico de la época William Thomson (1824-1907) conocido como Lord Kelvin, se atrevió a decir que solo dos pequeñas “nubecillas” arrojaban sombras sobre el majestuoso panorama de conocimiento que había construido la física clásica desde Galileo y Newton hasta ese momento: el resultado del experimento de Michelson-Morley, el cual había fallado en detectar la existencia del supuesto éter luminífero; y la radiación del cuerpo negro, i.e la incapacidad de la teoría electromagnética clásica de predecir la distribución de la energía radiante emitida a diferentes frecuencias emitidas por un radiador idealizado llamado cuerpo negro. Lo que Lord Kelvin no puedo predecir es que al tratar de disipar esas dos “nubecillas”, la física se vería irremediablemente arrastrada a una nueva física: la física moderna fundada sobre dos revoluciones en ciernes: la revolución relativista y la revolución cuántica con un científico protagonista en ambas: Albert Einstein.
Radiación del Cuerpo Negro
El primer atisbo del nuevo mundo cuántico se inicia en el transito de los siglos XIX y XX con el estudio de la emisión de radiación de cuerpo calientes. Así, la primera evidencia de la naturaleza cuántica (i.e discreta) de la radiación vino del estudio de la radiación térmica emitida por cuerpos opacos (aquellos que no son transparentes). Cuando la radiación lumínica incide sobre un cuerpo opaco, parte es reflejada, y el resto es absorbida. Los cuerpos que aparecen coloreados a la luz reflejan la mayoría de la radiación que incide sobre ellos, mientras que los cuerpos oscuros absorben la mayoría de ella. La radiación absorbida por un cuerpo incrementa la energía cinética de los átomos que constituyen el cuerpo, los cuales oscilan sobre sus posiciones de equilibrio. Dado que la energía de traslación promedio de los átomos determina la temperatura del cuerpo, la energía absorbida causa que la temperatura se incremente. No obstante, los átomos contienen cargas (electrones) y estos son acelerados por las oscilaciones. Consecuentemente como requiere la teoría electromagnética clásica los átomos emiten radiación electromagnética, la cual reduce la energía cinética de las oscilaciones y tiende a reducir la temperatura. Cuando la tasa de absorción iguala a la de emisión, la temperatura es constante y se dice que el cuerpo está en equilibrio térmico con su ambiente. Un buen absorbente de radiación es también un buen emisor, y a la inversa (Ley de Kirchhoff) esta es una de las razones por las que las paredes de los termos se construyen espejadas.
La radiación electromagnética emitida bajo estas circunstancias es llamada radiación térmica.Las superficie de un cuerpo material mantenido a una temperatura elevada emite luz de todas las frecuencias o longitudes de onda. Por lo tanto la radiación térmica es la radiación electromagnética emitida por un cuerpo en virtud de su temperatura. Dicha radiación presenta una distribución espectral (la emisión según las distintas frecuencias o longitudes de onda), cuya forma concreta depende depende de la temperatura establecida. A temperaturas ordinarias por debajo de 600ºC, la radiación térmica emitida por un cuerpo (e.g. una barra de hierro) de la energía emitida se concentra en longitudes de onda más largas que la de luz visible (en la zona infrarroja del espectro electromagnético), y los cuerpos son visibles por la luz que reflejan. Cuando el cuerpo es calentado, la cantidad de radiación térmica emitida se incrementa y la energía radiada se extiende a longitudes de onda cada vez más cortas, a una temperatura de aproximadamente 600-700 ºC, hay suficiente energía para ser emitida en el espectro visible por lo que el cuerpo empieza a resplandecer y aparece como un brillo rojo oscuro a temperaturas más altas (1200ºC) aparece como blanco azulado brillante, por encima de esa temperatura se emite ya radiación ultravioleta (UV) además de la visible e infrarroja.
El rango pues de longitudes de onda de la radiación térmica se sitúa entre las 0.1 μm y los 100μm, de este modo se extiende desde el ultravioleta hasta el infrarrojo, incluyendo por tanto la parte del visible del espectro electromagnético. Así. A temperaturas suficientemente altas, los cuerpos emiten radiación en la región del visible, y se hacen luminosos por si mismos mientras que, a bajas temperaturas, son visibles al ojo por la luz que reflejan y no por la emitida (que puede ser detectada con una cámara apropiada que es sensible a la radiación infrarroja).
Una superficie o cuerpo que absorbe toda la radiación que incide sobre ella se llama superficie de cuerpo negro ideal. Como este cuerpo no refleja nada, aparecerá negro a nuestros ojos. Un cuerpo negro también será un emisor ideal, y así la luz emitida por un cuerpo negro se llama radiación de cuerpo negro. Un cuerpo negro es por lo tanto una idealización, pues no existe ningún cuerpo real que cumpla las condiciones citadas. No obstante, en la naturaleza podemos encontrar cuerpos que se comportan aproximadamente como un cuerpo negro, un ejemplo de este tipo lo constituye un objeto que tiene una cavidad con paredes impermeables al calor lo más rugosas y ennegrecidas posibles que se comunica con el exterior con un pequeño orificio, es decir, un orificio que es pequeño comparado con las dimensiones finales de la cavidad. La radiación que, procedente del exterior, incida sobre dicho orificio penetrará en la cavidad, siendo absorbida por las paredes de ésta tras sucesivas reflexiones internas, si el tamaño del agujero es mucho más pequeño que el área total de dichas paredes, la probabilidad de que esta radiación vuelva a salir al exterior puede considerarse despreciable. El orificio se comporta como un absorbente perfecto. De otra forma la radiación térmica emergente hacia el exterior procedente de dicho agujero será espectralmente idéntica a la de un cuerpo negro a una determinada temperatura T, el agujero está pues absorbiendo toda la energía que le llega y por otra emitiendo la radiación correspondiente al equilibrio a la misma temperatura, el agujero puede ser considerado un cuerpo negro.
Para entender el concepto de cuerpo negro podemos pensar en una caja de cartón pintada en su interior de negro en la que se ha practicado un pequeño orificio en una de sus caras, visto desde fuera, el orificio resulta considerablemente “más negro” que cualquier superficie “negra” material.
En una medición de cuantitativa de la radiación de un cuerpo negro tenemos un recinto cerrado u “horno”, construido con un material adecuado, con un pequeño orificio en la pared . Se dirigen los instrumentos hacia el orificio y de esta manera medimos la energía radiante que emerge del interior del recinto. Llamada por ello también radiación de una cavidad. A partir de consideraciones termodinámicas muy generales el físico alemán Gustav R. Kirchhoff (1824-1887) quien en 1862 había introducido en la Física el concepto de cuerpo negro demostró que, para cualquier longitud de onda, la razón de la intensidad de emisión por una superficie arbitraria a la intensidad de emisión de una superficie de un cuerpo negro es igual al coeficiente de absorción del material para el valor de longitud de onda en cuestión. La superficie de cuerpo negro es, por lo tanto, un emisor patrón adecuado y se pueden limitar todas las consideraciones de la radiación térmica a la radiación que procede del orificio de una cavidad.
Ley de Stefan-Boltzmann
Así, en vez de estudiar la radiación procedente de una superficie material, cabe observar la radiación que procede de un pequeño orificio en la pared de una superficie material cerrada mantenida a una temperatura fija. En estas mediada experimentales se halló los siguientes hechos empíricos :
En 1879 el físico esloveno-austriaco Josef Stefan (1835-1893) encontró una relación empírica entre la potencia radiada por un cuerpo negro por unidad de área, llamada emitancia o poder emisivo R, dada en vatios por metro cuadrado (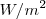 ) y la temperatura absoluta:
) y la temperatura absoluta:
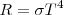
![[1] [1]](/images/math/math-f68b3e71cb9c9fc7184ee937f1d31000.png)
donde T es la temperatura absoluta en grados Kelvin, 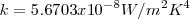 (en unidades de Sistema Internacional de Medidas: W, vatios; m metros, K, grados Kelvin) es una constante llamada de constante de Stefan-Bolztmann. Este resultado fue también derivado a través de consideraciones teóricas con base en la termodinámica clásica por un alumno de Stefan, el físico austriaco Ludwing Boltzmann (1844-1906) cinco años más tarde en 1884, por lo que la ecuación
(en unidades de Sistema Internacional de Medidas: W, vatios; m metros, K, grados Kelvin) es una constante llamada de constante de Stefan-Bolztmann. Este resultado fue también derivado a través de consideraciones teóricas con base en la termodinámica clásica por un alumno de Stefan, el físico austriaco Ludwing Boltzmann (1844-1906) cinco años más tarde en 1884, por lo que la ecuación ![[1] [1]](/images/math/math-7edb124f6e6e3c0bd88bf6282a8e603a.png) es llamada ley de Stefan-Boltzmann. Esta ecuación nos indica que la cantidad total de energía radiada (la emitancia total o poder emisivo total) por un cuerpo negro en equilibrio térmico aumenta con la cuarta potencia de su temperatura absoluta.
es llamada ley de Stefan-Boltzmann. Esta ecuación nos indica que la cantidad total de energía radiada (la emitancia total o poder emisivo total) por un cuerpo negro en equilibrio térmico aumenta con la cuarta potencia de su temperatura absoluta.
Los objetos que no son cuerpos negros radian energía por unidad de área a una tasa menor que la del cuerpo negro a la misma temperatura. Esa tasa dependen en otras propiedades además de la temperatura, tales como el color y la composición de la superficie. El efecto de estas dependencias es combinado en en un facto llamado emisividad  el cual debe ser incluido como factor multiplicador en la ecuación
el cual debe ser incluido como factor multiplicador en la ecuación ![[1] [1]](/images/math/math-7edb124f6e6e3c0bd88bf6282a8e603a.png) . El valor de
. El valor de  es también dependiente de la temperatura y siempre es menor que la unidad.
es también dependiente de la temperatura y siempre es menor que la unidad.
La distribución espectral de la radiación emitida por un cuerpo negro se encuentra que es empíricamente dependiente de la temperatura absoluta, mientras que la forma de la curva de emisión es independiente de la forma de la cavidad, como también, de la naturaleza del material de las paredes.
Al igual que el poder radiado total 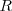 , la distribución espectral de la radiación emitida por un cuerpo negro se encuentra empíricamente que depende de la temperatura absoluta T. Si se representa para una determinada temperatura gráficamente el poder emitido por unidad de área
, la distribución espectral de la radiación emitida por un cuerpo negro se encuentra empíricamente que depende de la temperatura absoluta T. Si se representa para una determinada temperatura gráficamente el poder emitido por unidad de área 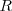 , en función de longitud de onda (
, en función de longitud de onda (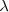 ) la llamada función de distribución espectral
) la llamada función de distribución espectral 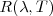 (la notación matemática expresa que la función
(la notación matemática expresa que la función 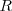 depende de las dos variables,
depende de las dos variables, 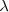 y T), se obtiene un curva acampanada lisa que tiende a cero tanto para longitudes de onda muy larga, como para longitudes de onda muy corta, en general la curva presenta un máximo para cierta longitud de onda
y T), se obtiene un curva acampanada lisa que tiende a cero tanto para longitudes de onda muy larga, como para longitudes de onda muy corta, en general la curva presenta un máximo para cierta longitud de onda 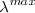 que depende de la temperatura absoluta T de manera muy simple:
que depende de la temperatura absoluta T de manera muy simple:
![\lambda^{max}T = Constante [Co]=2.898x10^{-3} m . K \lambda^{max}T = Constante [Co]=2.898x10^{-3} m . K](/images/math/math-8dc89a9acb3d266acfbcba39c24eda3d.png)
![[2] [2]](/images/math/math-ec736101c15bd1d1133c7e3d7015ddd9.png)
Este resultado expresa la ley de desplazamiento de Wien que fue obtenida por el físico alemán Wilhelm Wien (1864-1928). Desplazamiento en referencia al desplazamiento hacia longitudes de onda más corta que sufre el máximo de la curva conforme se incrementa la temperatura. Así, la longitud en la cual la distribución (emisión) es máxima varia inversamente con la temperatura. La constante 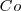 es una constante universal que describe una propiedad de las cavidades o superficies radiantes en general. La cantidad total de radiación emitida es más o menos la misma para todas las superficies materiales.
es una constante universal que describe una propiedad de las cavidades o superficies radiantes en general. La cantidad total de radiación emitida es más o menos la misma para todas las superficies materiales.
El poder radiado fuera del agujero 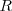 es proporcional a la densidad total de energía
es proporcional a la densidad total de energía 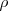 (energía por unidad de volumen de la radiación en la cavidad del cuerpo negro ideal). Se puede demostrar que la constante de proporcionalidad es igual
(energía por unidad de volumen de la radiación en la cavidad del cuerpo negro ideal). Se puede demostrar que la constante de proporcionalidad es igual 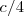 donde
donde  es la velocidad de la luz.
es la velocidad de la luz.
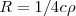
![[3] [3]](/images/math/math-5997f14afe377dff877df1d1629d9c02.png)
De igual manera la distribución espectral del poder emitido por el agujero es proporcional a la distribución espectral de la densidad de energía en la cavidad. Si 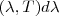 es la energía por unidad de volumen en la cavidad en el rango
es la energía por unidad de volumen en la cavidad en el rango 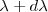 , entonces
, entonces 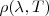 y
y 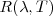 están relacionados por:
están relacionados por:
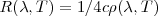
![[4] [4]](/images/math/math-b89757a59b41b6506218bd6647cd5ee7.png)
Esta relación se cumple para para cualquier cuerpo negro en equilibrio térmico. La función de distribución de densidad de energía 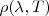 en el interior de la cavidad del cuerpo negro es completamente independiente de las propiedades y formas de los cuerpos puede que forma la pared del recinto del cuerpo negro. Por ello el espectro de radiación térmica emitido por un cuerpo negro en equilibrio térmico posee características universales. Una universalidad que cumple con el segundo principio de la termodinámica. Las funciones son por tanto funciones universales dependientes únicamente de la longitud de onda (o de la frecuencia ) y de la temperatura absoluta
en el interior de la cavidad del cuerpo negro es completamente independiente de las propiedades y formas de los cuerpos puede que forma la pared del recinto del cuerpo negro. Por ello el espectro de radiación térmica emitido por un cuerpo negro en equilibrio térmico posee características universales. Una universalidad que cumple con el segundo principio de la termodinámica. Las funciones son por tanto funciones universales dependientes únicamente de la longitud de onda (o de la frecuencia ) y de la temperatura absoluta 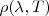 y
y 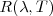 .
.
La función 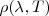 puede ser calculada a partir de la física clásica de manera sencilla. El método requiere encontrar el número de modos de oscilación del campo electromagnético en la cavidad con la longitud de onda en la cavidad en el intervalo
puede ser calculada a partir de la física clásica de manera sencilla. El método requiere encontrar el número de modos de oscilación del campo electromagnético en la cavidad con la longitud de onda en la cavidad en el intervalo 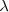 y multiplicando la energía promedio por nodo. El resultado es que el número de modos de oscilación por unidad de volumen n(
y multiplicando la energía promedio por nodo. El resultado es que el número de modos de oscilación por unidad de volumen n(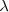 ) es independiente de la forma de la cavidad elegida y es dado por
) es independiente de la forma de la cavidad elegida y es dado por 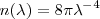
![[5] [5]](/images/math/math-311713d7e899562efc3b7c08c8a01ccb.png) . De acuerdo con la teoría cinética clásica la energía promedio por modo de oscilación es
. De acuerdo con la teoría cinética clásica la energía promedio por modo de oscilación es 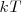 , la misma que para un oscilador armónico en una dimensión,
, la misma que para un oscilador armónico en una dimensión, 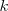 es la constante de Boltzmann
es la constante de Boltzmann 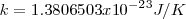 .
.
Ley de Rayleigh-Jeans
En el siglo XIX se habían realizado ya mediciones cuidadosas relativas a la ley de radiación del cuerpo negro. El principal problema teórico consistía en deducir la ley de la radiación a partir de los principios fundamentales de la física clásica.
Utilizando argumentos de electrodinámica clásica el físico inglés John-Willian Struct (Lord Rayleigh) (1842-1919) derivó y posteriormente fue modificada por sir James James (1877-1946) una función teórica de distribución espectral de densidad de energía 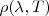 :
:
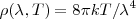
![[6] [6]](/images/math/math-efa651c624c49f90c998fb329daf1ea9.png) ; en función de la frecuencia
; en función de la frecuencia 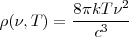
![[7] [7]](/images/math/math-c7e87f6a9b372fed3cdc993d50c13979.png) , llamada ley de Rayleigh-Jeans, donde
, llamada ley de Rayleigh-Jeans, donde 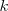 es la constante de Boltzmann.
es la constante de Boltzmann.
Esta ley muestra un serio conflicto entre las predicciones de la física clásica y los resultados experimentales. A muy bajas longitudes de onda esta ley estaba de acuerdo con la distribución espectral determinada experimentalmente, pero a longitudes de ondas corta de más alta frecuencia esta ley predice que 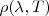 va incrementando de valor aproximándose a la infinidad cuando
va incrementando de valor aproximándose a la infinidad cuando 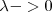 , mientras que experimentalmente se comprueba que la distribución se aproxima cero cuando
, mientras que experimentalmente se comprueba que la distribución se aproxima cero cuando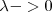 . Este enorme desacuerdo entre la mediada experimental de
. Este enorme desacuerdo entre la mediada experimental de 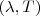 y la predicción fundamental de la física clásica a longitudes de onda corta fue llamada en 1911 por el físico austriaco, uno de los padres de la Teoría cuántica Paul S. Ehrenfest (1880-1933) la catástrofe ultravioleta, la ley de radiación Rayleigh-Jeans predecía una gran emisión de radiación ultravioleta UV por el cuerpo negro, cosa que experimentalmente no ocurre . Este comportamiento anómalo indicaría por ejemplo que seríamos abrasados por cualquier horno o pedazo de hierro incandescente , lo cual evidentemente no ocurre. O en palabras del físico y divulgador científico de origen ucraniano conocido con el nombre de George Gamov (1904-1968), “...al abrir la puerta del horno de una cocina o el cierre del hogar de una locomotora, seriamos alcanzado por la mortal radiación de las ondas cortas y moriríamos inmediatamente. La conclusión es evidentemente absurda , pero por otra parte resulta de la aplicación de las leyes fundamentales de la física clásica a la energía radiante.
y la predicción fundamental de la física clásica a longitudes de onda corta fue llamada en 1911 por el físico austriaco, uno de los padres de la Teoría cuántica Paul S. Ehrenfest (1880-1933) la catástrofe ultravioleta, la ley de radiación Rayleigh-Jeans predecía una gran emisión de radiación ultravioleta UV por el cuerpo negro, cosa que experimentalmente no ocurre . Este comportamiento anómalo indicaría por ejemplo que seríamos abrasados por cualquier horno o pedazo de hierro incandescente , lo cual evidentemente no ocurre. O en palabras del físico y divulgador científico de origen ucraniano conocido con el nombre de George Gamov (1904-1968), “...al abrir la puerta del horno de una cocina o el cierre del hogar de una locomotora, seriamos alcanzado por la mortal radiación de las ondas cortas y moriríamos inmediatamente. La conclusión es evidentemente absurda , pero por otra parte resulta de la aplicación de las leyes fundamentales de la física clásica a la energía radiante.
Así, la aplicación de las leyes básicas de la física clásica había conducido a la absurda ley de radiación de cuerpo negro que afirma que la intensidad de radiación radiada aumenta en monotonía con la frecuencia de tal manera que la intensidad radiada es total es infinita. Lo que significaría que la radiación no puede estar en equilibrio térmico con la materia, cualquiera que sea la temperatura, resultado teórico que evidentemente desmienten los hechos experimentales.
Planck y el inicio de la Revolución Cuántica
El catorce de diciembre del año 1900 en los albores del siglo XX, el físico alemán Max Planck (1858-1947) presentó un trabajo acerca de la ley de la radiación del cuerpo negro en una reunión de la Sociedad Alemana de Física, en Berlin, y esta fecha puede considerarse como el nacimiento de la física cuántica. En su deducción de la expresión teórica de la intensidad de radiación en función de la longitud de onda y de la temperatura, Planck abandonó la física clásica al introducir un hipótesis radical ad hoc cuya esencia puede formularse como sigue: Un oscilador de frecuencia natural  puede tomar o ceder energía únicamente en proporciones de magnitud
puede tomar o ceder energía únicamente en proporciones de magnitud 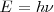
![[8] [8]](/images/math/math-041bd3d5f7775a49b25036b205a084f9.png) , donde
, donde 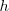 es una nueva constante de la naturaleza, llamada en honor de Planck constante de Planck (el cuanto de acción, pues tiene dimensiones de acción (energía por tiempo) J.s; Julios (J), unidad de energía por segundo (s) unidad de tiempo) y solo puede tener, y por lo tanto solo emitir energía dadas por
es una nueva constante de la naturaleza, llamada en honor de Planck constante de Planck (el cuanto de acción, pues tiene dimensiones de acción (energía por tiempo) J.s; Julios (J), unidad de energía por segundo (s) unidad de tiempo) y solo puede tener, y por lo tanto solo emitir energía dadas por 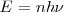
![[9] [9]](/images/math/math-9c181ce514a5b3b7448bf286d22938e4.png) , donde
, donde  es un entero positivo,
es un entero positivo,  la frecuencia de la radiación. Planck fue capaz con esta hipótesis encontrar una expresión teórica para la función de distribución espectral de densidad energía en función de la longitud de onda
la frecuencia de la radiación. Planck fue capaz con esta hipótesis encontrar una expresión teórica para la función de distribución espectral de densidad energía en función de la longitud de onda 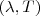 o de la frecuencia
o de la frecuencia 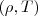 de la radiación de la cavidad del cuerpo negro:
de la radiación de la cavidad del cuerpo negro:
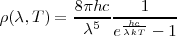
![[10] [10]](/images/math/math-72c6de23946c890c5f38892fa34fa37a.png)
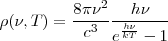
![[11] [11]](/images/math/math-d453df59240d501fbe009575ed8356a7.png)
Donde 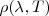 es la densidad de energía radiante en la cavidad por unidad de intervalo de longitud de onda, para la longitud de onda
es la densidad de energía radiante en la cavidad por unidad de intervalo de longitud de onda, para la longitud de onda 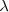 , a la tempera absoluta
, a la tempera absoluta 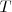 , la constante
, la constante 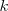 es la constante de Boltzmann, y
es la constante de Boltzmann, y  es la velocidad de la luz, y
es la velocidad de la luz, y 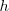 es la constante de Planck.
es la constante de Planck.
Esta función llamada ley de Planck se ajustaba muy bien a los datos obtenidos experimentalmente. El valor de la constante de Planck 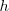 , puede ser determinado encajando la función de la ecuación a los datos experimentales. El valor actual aceptado para la constante
, puede ser determinado encajando la función de la ecuación a los datos experimentales. El valor actual aceptado para la constante 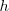 es igual:
es igual:
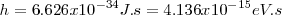
La importancia fundamental, la explicación física de la cuantificación o cuantización (discretización) introducida por la ecuación ![[10] [10]](/images/math/math-72c6de23946c890c5f38892fa34fa37a.png) ,
, ![[11] [11]](/images/math/math-d453df59240d501fbe009575ed8356a7.png) no fue completamente entendida por Planck que la consideraba simplemente solo un truco matemático para ajustar una función matemática a los datos físicos. Planck era un físico formado en la tradición clásica, y que solo abandono los supuestos clásicos “en un acto de desesperación” como el dijo alguna vez. El significado físico de la entrada del cuanto de acción en la escena física, no fue generalmente apreciada por los físicos hasta 1905, cuando el genial físico de origen alemán Albert Einstein (1879-1955) aplicó las ideas cuánticas de Planck a la explicación del efecto fotoeléctrico, al sugerir que la misma no era una misteriosa propiedad de los osciladores en las paredes de la cavidad y la radiación de cuerpo negro, la cuantificación es una característica fundamental de la propia energía lumínica[[1]].
no fue completamente entendida por Planck que la consideraba simplemente solo un truco matemático para ajustar una función matemática a los datos físicos. Planck era un físico formado en la tradición clásica, y que solo abandono los supuestos clásicos “en un acto de desesperación” como el dijo alguna vez. El significado físico de la entrada del cuanto de acción en la escena física, no fue generalmente apreciada por los físicos hasta 1905, cuando el genial físico de origen alemán Albert Einstein (1879-1955) aplicó las ideas cuánticas de Planck a la explicación del efecto fotoeléctrico, al sugerir que la misma no era una misteriosa propiedad de los osciladores en las paredes de la cavidad y la radiación de cuerpo negro, la cuantificación es una característica fundamental de la propia energía lumínica[[1]].
Bibliografía
George Gamow. Biografía de la Física. Alianza Editorial.1980. Una explicación deliciosa de los entresijos de la física clásica y moderna.
Hey, T & Walter Patrick. El Universo Cuántico, Alianza Editorial. 1989. Una completa entrada en el mundo cuántico.
Sánchez del Rio (coordinador). Física Cuántica. Ediciones Pirámide. 1997 . Un libro sobre física cuántica escrito por varios físicos españoles.
Paul.A.Tipler & Ralph A. Lewellyn. Modern Physics.W.H. Freeman Company. New York. Third Edition.1999. Un clásico de los libros de texto de física moderna.
Enlaces externos
Hyperphysics: Blackbody Radiation [[2]]
Tweet


