Dualidad de la materia. De Broglie
De Wikillerato
(Página nueva: <h4>Antecedentes históricos</h4> Hasta la primera veintena de años del siglo XX, la física había descubierto a las claras que la naturaleza física de la radiación (luz) mostrab...) |
|||
| Línea 21: | Línea 21: | ||
Para fotones la relación de De Broglie resultan a partir de la ecuación de Einstein de la cuantización de la Energía: | Para fotones la relación de De Broglie resultan a partir de la ecuación de Einstein de la cuantización de la Energía: | ||
| - | + | <math>E=h\nu</math> <math>[2]</math> | |
y de la [[ecuación relativista]] que relaciona la energía de un partícula con su masa y su momento: | y de la [[ecuación relativista]] que relaciona la energía de un partícula con su masa y su momento: | ||
| Línea 27: | Línea 27: | ||
<math>E^2=(pc)^2+ (mc^2)^2 </math> <math>[3]</math> | <math>E^2=(pc)^2+ (mc^2)^2 </math> <math>[3]</math> | ||
| - | para una partícula de masa en reposo <math>m= | + | para una partícula de masa en reposo <math>m=0</math> como el fotón, por lo que la parte <math>(mc^2)^2</math> es igual a cero, y entonces tenemos que despejando <math>p</math> en la ecuación <math>[3]</math> que el momento del fotón vale: |
<math>p=\frac{E}{c}</math> <math>[4]</math> | <math>p=\frac{E}{c}</math> <math>[4]</math> | ||
| - | Por otra parte <math>E=h\nu=\frac{hc}{\lambda} | + | Por otra parte tenemos que <math>E=h\nu=\frac{hc}{\lambda} </math> <math>[5]</math> |
| - | + | así que | |
| - | + | <math>p=\frac{hc}{c\lambda}=\frac{h}{\lambda}</math> <math>[6]</math> | |
| - | + | Las relaciones momento-longitud de onda para una partícula como un fotón pueden ser derivadas así de esta forma y De Broglie propuso que las relación de momento-longitud de onda se aplica a otra partículas también. es decir, De Broglie propuso que la relación era universalmente aplicable. Así, la relacion de De Broglie se pueden aplicar de manera universal a cualquier entidad particular que tenga momento: fotones, electrones, neutrones, protones, DNA, etc.... | |
| - | <math>\lambda | + | Así, depejando <math>\lambda</math> en la ecuación <math>[6]</math> tenemos la relación de De Broglie |
| - | + | <math>\lambda=\frac{h}{p}=\frac{h}{mv}</math> | |
| - | + | De Broglie indicó además que esas relaciones conducirían a a una interpretación física de la cuantización de las órbitas electrónicas que Niels Bohr introdujo en su modelo atómico, a saber que la cuantización es equivalente a una condición de'' onda estacionaria'', ondas que satisfacen la condición de que su longitud contiene un número entero de longitudes de onda <math>\lambda</math>, una onda en la primera órbita cuántica, dos en la segunda , etc... | |
| - | <math> | + | |
| - | + | ||
| - | + | ||
| - | El significado de las relaciones de De Broglie es que en ella se resumen una “fusión de opuestos”: el momento <math>p</math> es un propiedad de las partículas; mientras que la longitud de onda (\lambda) es una propiedad de las ondas. Está dualidad, la posesión de propiedades que la físca clásica son características de ambas partículas y ondas, es un tema persistente en la interpretación de la mecánica cuántica. | + | Si tenemos la condición de cuantización del momento angular orbital del electrón de Bohr: |
| + | |||
| + | <math>L=mvr=n\hbar=\frac{nh}{2\pi}</math> con <math>n=1,2,3...</math> <math>[7]</math> | ||
| + | |||
| + | despejando, y teniendo en cuenta la relación de De Broglie: | ||
| + | |||
| + | <math>2\pi r=\frac{nh}{mv}=\frac{nh}{p}=n\lambda=C</math> <math>[8]</math> | ||
| + | |||
| + | Donde <math>C</math> es la circunferencia de la órbita | ||
| + | |||
| + | En palabras de físico cuántico y divulgador científico George Gamov,:”... para las órbitas intermedias [aquellas que podrían existir entre las órbitas estacionarias] , una “onda de materia piloto” corriendo en un circulo “no puede morderse” la cola , y en consecuencia no puede existir este tipo de movimiento. De Broglie cambió las “órbitas esqueléticas” de Bohr por una “carnosa” noción de tubos de órgano, membranas de tambor, etc...la mecánica cuántica de partículas adquirió propiedades semejantes a las ondas sonoras o luminosas” (b). | ||
| + | |||
| + | El significado de las relaciones de De Broglie es que en ella se resumen una “fusión de opuestos”: el momento <math>p</math> es un propiedad de las partículas; mientras que la longitud de onda (<math>\lambda</math>) es una propiedad de las ondas. Está dualidad, la posesión de propiedades que la físca clásica son características de ambas partículas y ondas, es un tema persistente en la interpretación de la mecánica cuántica. | ||
| + | |||
Así, la idea de explicar los estados de energía discretos en la materia por ondas estacionarias era una idea muy prometedora, pues explicaba de manera natural a existencia de cuantización. | Así, la idea de explicar los estados de energía discretos en la materia por ondas estacionarias era una idea muy prometedora, pues explicaba de manera natural a existencia de cuantización. | ||
La ideas de De Broglie fueron expandidas y desarrolladas en una completa teoría (llamada inicialmente “mecánica cuántica de ondas”) por Erwing Schrödinger en 1925. | La ideas de De Broglie fueron expandidas y desarrolladas en una completa teoría (llamada inicialmente “mecánica cuántica de ondas”) por Erwing Schrödinger en 1925. | ||
| - | |||
<h4>Verificación experimental de la hipótesis de De Broglie</h4> | <h4>Verificación experimental de la hipótesis de De Broglie</h4> | ||
Revisión de 18:16 29 nov 2008
Tabla de contenidos |
Antecedentes históricos
Hasta la primera veintena de años del siglo XX, la física había descubierto a las claras que la naturaleza física de la radiación (luz) mostraba un aspecto dual de comportamiento onda-corpúsculo. Así, por una parte los fenómenos de difracción e interferencia indicaban claramente que la luz consistía en ondas electromagnéticas, su carácter ondulatorio; pero por otra parte fenómenos como el efecto fotoeléctrico y el efecto Compton, solo se podían explicar adecuadamente si la luz era considerada como un conjunto de paquetes discretos, quanta (singular quantum ), cuantos o fotones de energía lumínica, su carácter corpuscular. Un noble francés, llevaría un paso más adelante esa dualidad onda-corpúsculo al situar la misma no solo en la radiación lumínica sino también en la propia materia.
Hipótesis de De Broglie
En el año 1924 un joven aristócrata francés, el marqués Louis de Broglie (1892-1987) presentó un trabajo de Tesis Doctoral, titulada Recherches sur la théorie des quanta (Investigaciones sobre la teoría cuántica) por el que reclamaba el título de Doctor, y que estaba llena de ideas insólitas (solo después de la intercesión de Einstein, De Broglie obtuvo su título de Doctor, por el cual además obtuvo el Premio Nobel en 1929).
De Broglie había comenzado su carrera científica como estudiante de historia medieval y solo después de servir como ingeniero de radio en la armada francesa se interesó por la ciencia y por la física teórica de la mano de su hermano también físico Murice De Broglie. Entre las ideas y audaces encontradas en su Tesis Doctoral se encontraba la propuesta (hipótesis) de que el comportamiento dual característico que hasta entonces se había conocido para la radiación lumínica (luz) podía ser una característica esencial de la materia, en particular para los electrones. Hasta la fecha no había ninguna prueba experimental que pudiera corroborar esa idea tan especulativa, a la cual De Broglie fue llevada por un “penetrante intuición”, como “un rayo en el cielo”o como decía Einstein por un “pensamiento feliz” (del mismo que le llevó a él al principio de equivalencia).
En palabras de De Broglie:
“...Después de que terminara la primera guerra mundial, pensé en profundidad sobre los quanta y el dualismo onda-cospúsculo...y fue entonces cuando tuve una súbita inspiración, el dualismo onda-corpúsculo de Einstein era un fenómeno absolutamente general que se extendía a toda la Naturaleza física” (a).
De Broglie apoyó su intuitiva propuesta matemáticamente (en Ciencia, sin matemáticas que respalden las ideas intuitivas, estas se suelen quedar sin ser consideradas seriamente) con la siguiente ecuacione para 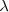 la longitud de onda de las ondas electrónicas o más generalmente ondas de materia, ecuación la cuale es ahora conocida como relación de De Broglie o relación momento-longitud:
la longitud de onda de las ondas electrónicas o más generalmente ondas de materia, ecuación la cuale es ahora conocida como relación de De Broglie o relación momento-longitud:
Donde 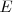 es la energía,
es la energía,  es el momento,
es el momento, 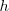 es la constante de Planck y
es la constante de Planck y 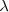 es la llamada longitud de onda de De Broglie, la cual es inversamente proporcional al momento de la partícula. Con estas ecuaciones la contante de Planck y el quatum fueron introducidos también en la materia. De Broglie alcanzó dichas ecuaciones en base a consideraciones relativistas, siguiendo un desarrollo matemático similar a aquel por el que se obtiene el momento de un fotón. Veamos como:
es la llamada longitud de onda de De Broglie, la cual es inversamente proporcional al momento de la partícula. Con estas ecuaciones la contante de Planck y el quatum fueron introducidos también en la materia. De Broglie alcanzó dichas ecuaciones en base a consideraciones relativistas, siguiendo un desarrollo matemático similar a aquel por el que se obtiene el momento de un fotón. Veamos como:
Para fotones la relación de De Broglie resultan a partir de la ecuación de Einstein de la cuantización de la Energía:
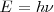
![[2] [2]](/images/math/math-ec736101c15bd1d1133c7e3d7015ddd9.png)
y de la ecuación relativista que relaciona la energía de un partícula con su masa y su momento:
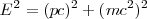
![[3] [3]](/images/math/math-5997f14afe377dff877df1d1629d9c02.png)
para una partícula de masa en reposo 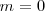 como el fotón, por lo que la parte
como el fotón, por lo que la parte 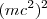 es igual a cero, y entonces tenemos que despejando
es igual a cero, y entonces tenemos que despejando  en la ecuación
en la ecuación ![[3] [3]](/images/math/math-5997f14afe377dff877df1d1629d9c02.png) que el momento del fotón vale:
que el momento del fotón vale:
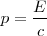
![[4] [4]](/images/math/math-b89757a59b41b6506218bd6647cd5ee7.png)
Por otra parte tenemos que 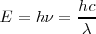
![[5] [5]](/images/math/math-311713d7e899562efc3b7c08c8a01ccb.png)
así que
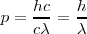
![[6] [6]](/images/math/math-efa651c624c49f90c998fb329daf1ea9.png)
Las relaciones momento-longitud de onda para una partícula como un fotón pueden ser derivadas así de esta forma y De Broglie propuso que las relación de momento-longitud de onda se aplica a otra partículas también. es decir, De Broglie propuso que la relación era universalmente aplicable. Así, la relacion de De Broglie se pueden aplicar de manera universal a cualquier entidad particular que tenga momento: fotones, electrones, neutrones, protones, DNA, etc....
Así, depejando 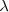 en la ecuación
en la ecuación ![[6] [6]](/images/math/math-efa651c624c49f90c998fb329daf1ea9.png) tenemos la relación de De Broglie
tenemos la relación de De Broglie
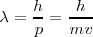
De Broglie indicó además que esas relaciones conducirían a a una interpretación física de la cuantización de las órbitas electrónicas que Niels Bohr introdujo en su modelo atómico, a saber que la cuantización es equivalente a una condición de onda estacionaria, ondas que satisfacen la condición de que su longitud contiene un número entero de longitudes de onda 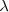 , una onda en la primera órbita cuántica, dos en la segunda , etc...
, una onda en la primera órbita cuántica, dos en la segunda , etc...
Si tenemos la condición de cuantización del momento angular orbital del electrón de Bohr:
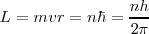 con
con 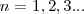
![[7] [7]](/images/math/math-c7e87f6a9b372fed3cdc993d50c13979.png)
despejando, y teniendo en cuenta la relación de De Broglie:
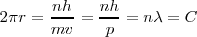
![[8] [8]](/images/math/math-041bd3d5f7775a49b25036b205a084f9.png)
Donde  es la circunferencia de la órbita
es la circunferencia de la órbita
En palabras de físico cuántico y divulgador científico George Gamov,:”... para las órbitas intermedias [aquellas que podrían existir entre las órbitas estacionarias] , una “onda de materia piloto” corriendo en un circulo “no puede morderse” la cola , y en consecuencia no puede existir este tipo de movimiento. De Broglie cambió las “órbitas esqueléticas” de Bohr por una “carnosa” noción de tubos de órgano, membranas de tambor, etc...la mecánica cuántica de partículas adquirió propiedades semejantes a las ondas sonoras o luminosas” (b).
El significado de las relaciones de De Broglie es que en ella se resumen una “fusión de opuestos”: el momento  es un propiedad de las partículas; mientras que la longitud de onda (
es un propiedad de las partículas; mientras que la longitud de onda (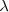 ) es una propiedad de las ondas. Está dualidad, la posesión de propiedades que la físca clásica son características de ambas partículas y ondas, es un tema persistente en la interpretación de la mecánica cuántica.
) es una propiedad de las ondas. Está dualidad, la posesión de propiedades que la físca clásica son características de ambas partículas y ondas, es un tema persistente en la interpretación de la mecánica cuántica.
Así, la idea de explicar los estados de energía discretos en la materia por ondas estacionarias era una idea muy prometedora, pues explicaba de manera natural a existencia de cuantización. La ideas de De Broglie fueron expandidas y desarrolladas en una completa teoría (llamada inicialmente “mecánica cuántica de ondas”) por Erwing Schrödinger en 1925.
Verificación experimental de la hipótesis de De Broglie
Experimento de Davisson-Germer
Bibliografía
(a).- Cita , traducida del inglés, obtenida del libro:
Paul.A.Tipler & Ralph A. Lewellyn. Modern Physics.W.H. Freeman Company. New Tork Third Edition.1999. Un clásico de los libros de texto de física moderna
(b) .- Cita obtenida del libro George Gamov. Biografía de la Física. Alianza Editorial. 1980.
Enlaces externos
Lectura del premio Nobel de De Broglie: [[1]]
Hiperphysics: the De Broglie Hypothesis: [[2]]
Tweet

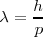
![[1] [1]](/images/math/math-7edb124f6e6e3c0bd88bf6282a8e603a.png)

