La ley de Einstein del efecto fotoeléctrico
De Wikillerato
| (9 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | En su artículo Einstein daba una explicación teórica a varias de las propiedades hasta entonces misteriosas de la luz, y que no eran explicables por la teoría clásica electromagnética proponiendo la hipótesis (revolucionaria para aquel tiempo) de que la '''radiación lumínica está cuantizada''', esto es es la luz emitida por los objetos radiantes está formada de '''paquetes discretos de energía''', llamados ''quanta'' (singular'' quantum'' , del latín, cantidad), '''cuantos de luz''' (''das Lichtquant'' como los llamó Einstein) con una energía | + | En su artículo Einstein daba una explicación teórica a varias de las propiedades hasta entonces misteriosas de la luz, y que no eran explicables por la teoría clásica electromagnética proponiendo la hipótesis (revolucionaria para aquel tiempo) de que la '''radiación lumínica está cuantizada''', esto es es la luz emitida por los objetos radiantes está formada de '''paquetes discretos de energía''', llamados ''quanta'' (singular '' quantum'' , del latín, cantidad), '''cuantos de luz''' (''das Lichtquant'' como los llamó Einstein en alemán) con una energía <math>E= h\nu</math> (siendo <math>h</math> la '''constante de Planck''', y <math>\nu</math>, la frecuencia de la radiación electromagnética), posteriormente denominados '''fotones''' (partículas de luz), en 1926 por el físicoquímico norteamericano Gilbert N. Lewis (1875 -1946) . |
| - | Así, Einstein asumió que la cuantización de la emisión de la energía usada por el físico alemán Max Planck (1858 - 1947 ) para explicar '''el espectro de la radiación de cuerpo negro''' en 1900 es una característica universal de la luz. Max Planck en su artículo fundacional de la era cuántica (donde introdujo la expresión | + | Así, Einstein asumió que la cuantización de la emisión de la energía usada por el físico alemán Max Planck (1858 - 1947) para explicar '''el espectro de la radiación de cuerpo negro''' en 1900 es una característica universal de la luz. Max Planck en su artículo fundacional de la era cuántica (donde introdujo la expresión <math>E= h\nu</math> ) había colocado esa discontinuidad en el emisor de la radiación no en la radiación misma. Einstein coloco de esta manera la '''discontinuidad cuántica''' en la misma luz (radiación electromagnética). De esta manera, más bien que estar distribuida continuamente por el espacio a través del cual se propaga, la energía de la luz consiste de quanta discretos de energía. La luz actúa igual que pequeñas partículas al interaccionar con la materia. |
| - | En el efecto fotoeléctrico, es pues un '''efecto mecanocuántico''', en el que se produce fotoemisión de electrones cuando uno de los ''quantum'' (fotón) de energía h<math>\nu</math> es absorbido por un electrón del metal. El hecho de que la energía de expulsión de los electrones fuera independiente de la energía total de iluminación, se explica bien si consideramos que la interacción de la luz con los electrones del metal debe ser igual que una partícula que da toda la energía al electrón. Así, cuando uno de estos fotones penetran en la superficie del cátodo toda la energía puede darse completamente al electrón, la energía del fotón es convertida en energía del fotoelectrón. No obstante, si el electrón está alguna distancia en el material del cátodo, alguna energía será perdida en el movimiento hacia la superficie. Esto es, el electrón debe utilizar cierta energía para escapar del metal, siempre habrá un coste cuando el electrón deja la superficie del cátodo, llamado por ello la '''función de trabajo fotoeléctrico''' W , igual a la '''energía de ionización''' del metal, la energía necesaria para extraer un electrón del metal, y que es característica de cada metal. | + | En el efecto fotoeléctrico, es pues un '''efecto mecanocuántico''', en el que se produce fotoemisión de electrones cuando uno de los ''quantum'' (fotón) de energía h<math>\nu</math> es absorbido por un electrón del metal. El hecho de que la energía de expulsión de los electrones fuera independiente de la energía total de iluminación, se explica bien si consideramos que la interacción de la luz con los electrones del metal debe ser igual que una partícula que da toda la energía al electrón. Así, cuando uno de estos fotones penetran en la superficie del cátodo toda la energía puede darse completamente al electrón, la energía del fotón es convertida en energía del fotoelectrón. No obstante, si el electrón está alguna distancia en el material del cátodo, alguna energía será perdida en el movimiento hacia la superficie. Esto es, el electrón debe utilizar cierta energía para escapar del metal, siempre habrá un coste cuando el electrón deja la superficie del cátodo, llamado por ello la '''función de trabajo fotoeléctrico''' <math> W </math> , igual a la '''energía de ionización''' del metal, la energía necesaria para extraer un electrón del metal, y que es característica de cada metal. |
| - | Los electrones más energéticos serán aquellos emitidos desde la superficie del metal, y dejaran el cátodo con una energía cinética Ec= | + | Los electrones más energéticos serán aquellos emitidos desde la superficie del metal, y dejaran el cátodo con una energía cinética <math>Ec=\frac{mv^2}{2}</math> ; la cual representa la diferencia <math>Ec = h\nu - W </math> , una consecuencia de la conservación de la energía . Algunos electrones tendrán menos energía cinética de esta cantidad debida a la energía perdida dentro del metal. |
La ecuación de Einstein del efecto fotoeléctrico expresa estos hechos: | La ecuación de Einstein del efecto fotoeléctrico expresa estos hechos: | ||
| - | + | <math>h\nu= Ec+ W </math> <math>[1]</math> | |
| - | La energía de un cuanto de luz (h<math>\nu</math>) incidente es igual a la energía requerida para extraer el electrón del metal (la función W) más la energía cinética | + | La energía de un cuanto de luz (h<math>\nu</math>) incidente es igual a la energía requerida para extraer el electrón del metal (la función <math>W</math>) más la energía cinética <math>Ec=\frac{1}{2}mv^2</math> impartida al electrón. |
| - | Es difícil medir directamente la velocidad de los electrones, en su lugar la cantidad 1/ | + | Es difícil medir directamente la velocidad de los electrones, en su lugar la cantidad <math>Ec=\frac{1}{2}mv^2</math>, la energía cinética del electrón es determinada midiendo la diferencia de potencial <math>V</math>, que es necesaria para impedir que los electrones lleguen la ánodo. El producto de de la diferencia de potencial V por la carga del electrón e es la cantidad de trabajo hecho contra el campo electrostático, y cuando <math>V</math> tiene justo el valor requerido para prevenir que los electrones alcancen el ánodo (llamado entonces potencial de parada <math>V_o</math>) la siguiente relación es satisfecha <math>eV_o=\frac{1}{2} mv^2</math> es la energía cinética <math>Ec</math> con la que el electrón abandona la superficie del metal, energía que es medida por el producto de la carga <math>e</math> del electrón por la diferencia de potencial, contra la cual está en condiciones de moverse antes de detenerse. Experimentalmente se puede ajustar el voltaje negativo de la placa colectora (ánodo) hasta que la corriente (de los electrones) se detenga, esto es que se alcance el potencial de parada (Vo), la energía cinética de los electrones deben tener la energía <math>eVo</math> al dejar el cátodo. El potencial de parada <math>V_o</math> será dado por |
| - | + | <math>eV_o= h\nu- W </math> <math>[2]</math> | |
| - | Esta ecuación es otra manera de expresar la ecuación de Einstein del efecto fotoelectrico (realmente es la que Einstein en su notación matemática Πε= R/Nβ <math>\nu</math>-P dio en su artículo de 1905), La frecuencia mínima o umbral <math>\nu_o</math>para el efecto fotoeléctrico está relacionada a longitud de onda (λo) de la radiación incidente y a la función de trabajo W si Vo=0 es igual | + | Esta ecuación es otra manera de expresar la ecuación de Einstein del efecto fotoelectrico (realmente es la que Einstein en su notación matemática Πε= R/Nβ <math>\nu</math>-P dio en su artículo de 1905), La frecuencia mínima o umbral <math>\nu_o</math>para el efecto fotoeléctrico está relacionada a longitud de onda (λo) de la radiación incidente y a la función de trabajo<math> W</math> si <math>Vo=0</math> es igual: |
| - | + | <math>W=h\nu_o=h\frac{c}{\lambda_o}</math> <math>[3]</math> | |
| - | c, es la velocidad de la luz | + | <math>c</math>, es la velocidad de la luz; <math>\lambda_o</math>, la longitud de onda umbral, (<math>\nu_o</math>) la frecuencia umbral es la frecuencia de la luz a la cual el cuanto de luz tiene la energía precisa para arrancar un electrón del metal, si un cuanto de luz tiene una frecuencia más grande ( <math>\nu_o > \nu</math>) es capaz de arrancar los electrones del metal y darlos además alguna energía cinética. Fotones con frecuencia más baja que la frecuencia umbral (<math>\nu_o>\nu</math>) y por lo tanto teniendo una longitud de onda mayor que la umbral (<math>\lambda>\lambda_o</math>) no tendrán la suficiente energía para expulsar los fotones del metal. Una vez que la frecuencia umbral es alcanzada, la corriente electrónica se incrementa linealmente con la intensidad de la radiación que puede ser medida en el amperimetro conectado al circuito. |
| - | Diferentes sustancia metálicas tienen frecuencias | + | Diferentes sustancia metálicas tienen frecuencias umbrales <math>\nu_o</math>fotoelétricas diferentes: los metales alcalinos son muy buenos emisores fotoeléctricos y su umbral está en la región del visible; para el sodio (Na) esta λo es aproximadamente de <math>650 nm</math>, así que la energía visible es efectiva con este metal excepto en la parte rojo del región visible del espectro electromagnético.Así, una la luz roja de longuitud de onda <math>\lambda</math> de <math>700 nm</math> por ejemplo no causa emisión de los electrones independiente de la intensidad de luz aplicada. Por otra parte, una luz débil ultravioleta <math>\lambda=400 nm</math> provocará la emisión de pocos electrones, pero el máximo de energía cinética de los electrones eyectados será más grande que aquellos que son expulsados por una luz muy intensa pero de más larga longitud de onda y menor frecuencia. |
| - | En la ecuación de Einstein | + | En la ecuación de Einstein, <math>eV_o=h\nu-W</math>, la pendiente de la recta <math>V_o</math> versus <math>\nu</math> sería igual a <math>\frac{e}{h}</math>. En el tiempo que Einstein hizo esta predicción, no había ninguna evidencia de que la constante de Planck tuviera nada que ver con el efecto fotoeléctrico. Tampoco había ninguna evidencia de la dependencia del potencial de parada <math>Vo</math> con la frecuencia <math>\nu</math>. Los experimentos del físico norteamericano Robert Andrews Millikan (1868 -1953) (por los que ganó el premio Nobel de Física 1923) mostraron que la ecuación de Einstein para el efecto fotoeléctrico era correcta y el valor de h estaba de acuerdo con el que había obtenido Planck. El valor obtenido por Millikan fue durante muchos años el valor más preciso conocido. |
El valor más preciso aceptado de la constante Planck hasta la fecha es: | El valor más preciso aceptado de la constante Planck hasta la fecha es: | ||
| - | |||
| - | + | <math>h=6.62606896 x10^{-34} J.s </math> donde <math>J.s</math> (Julios por segundo) es una unidad física de '''acción''' [energía x tiempo]. | |
| - | + | El valor de <math>h</math> está obtenido del NIST [http://physics.nist.gov/cgi-bin/cuu/Value?h|search_for=universal_in!]] | |
| - | Otro de las característica intrigantes del efecto fotoeléctrico que no podía explicar la teoría clásica de la física pero fácilmente explicable por la hipótesis de Einstein del fotón es la carencia de lapso de tiempo entre la emisión incidencia de la luz y la aparición de los electrones. La hipótesis de Einstein explica este resultado ya que aunque cada fotón tiene la energía suficiente para eyectar un electrón (el cuanto de luz puede transferir su energía integra a un electrón) , habiendo una probabilidad de que el electrón sea rápidamente e inmediatamente absobido por un electrón acompañado de la emisión instantánea del mismo. Esto es cuando un electrón captura la energía de un un fotón, la emisión del mismo es instantanea siempre que la energía del fotón tenga la suficiente energía. Si un fotón no tiene suficiente energía, el electrón no será capaz de salir del metal. | + | La constante <math>\frac {h}{4\pi}</math> [o también expresado como <math>\frac{\hbar}{2}</math>; con <math>\hbar=\frac{h}{2\pi}</math>] representa el '''cuanto mínimo de acción'''. En la naturaleza las acciones (una mediada del cambio) más pequeñas que esas no han sido observadas, la existencia de esta ''mínima cantidad de acción'', implica además que siempre hay un cambio mínimo en los cambios de la naturaleza (''principio cuántico''). |
| + | |||
| + | Otro de las característica intrigantes del efecto fotoeléctrico que no podía explicar la teoría clásica de la física pero fácilmente explicable por la hipótesis de Einstein del fotón es la carencia de lapso de tiempo entre la emisión incidencia de la luz y la aparición de los electrones. La hipótesis de Einstein explica este resultado ya que aunque cada fotón tiene la energía suficiente para eyectar un electrón (el cuanto de luz puede transferir su energía integra a un electrón), habiendo una probabilidad de que el electrón sea rápidamente e inmediatamente absobido por un electrón acompañado de la emisión instantánea del mismo. Esto es cuando un electrón captura la energía de un un fotón, la emisión del mismo es instantanea siempre que la energía del fotón tenga la suficiente energía. Si un fotón no tiene suficiente energía, el electrón no será capaz de salir del metal. | ||
El éxito de la ecuación de Einstein en explicar las observaciones experimentales del efecto foelectrico fue en gran parte la responsable de la aceptación de la idea de los quanta de luz. | El éxito de la ecuación de Einstein en explicar las observaciones experimentales del efecto foelectrico fue en gran parte la responsable de la aceptación de la idea de los quanta de luz. | ||
| Línea 40: | Línea 41: | ||
===Moraleja epistemiologica de la historia del efecto fotoeléctrico=== | ===Moraleja epistemiologica de la historia del efecto fotoeléctrico=== | ||
| - | La historia del efecto fotoeléctrico representa de manera muy viva como funciona la investigación científica, la interrelación estrecha que existe entre Teoría y Experimento. Heinrich Hetz diseñó un aparato experimental para producir y detectar ondas electromagnéticas tal como se predecía en la teoría electromagnética de Maxwell (una notable aplicación del método hipotético-deductivo en Ciencia), al detectarlas confirmó de manera inequívoca la teoría de este, y por lo tanto la '''naturaleza ondulatoria de la luz''', pero por otra parte la historia nos enseña como la aparición de un nuevo fenómeno experimental no previsto (cuando esto ocurre se dice que fue descubierto por '''serendipia'''), mientras se realizaba el experimento fundamental espolea la búsqueda de una explicación teórica adecuada del mismo, explicación que la propia teoría clásica de Maxwell fue incapaz de ofrecer en el caso del efecto fotoelectrico, y solo con la explicación cuántica de Einstein, lo que suponía salirse del marco conceptual y teórico continuista, de la física clásica (llamado por el epistemiologo Thomas Samuel Kuhn (1922 - 1996 ) '''paradigma''', en su famoso libro: ''La Estructura de las Revoluciones Científicas'') y adentrarse en un nuevo marco conceptual de discontinuidad mecanicocuántica poniendo de manifiesto la''' dualidad básica onda-corpúsculo''' característica esencial de la naturaleza física de la luz. | + | La historia del efecto fotoeléctrico representa de manera muy viva como funciona la investigación científica, la interrelación estrecha que existe entre Teoría y Experimento. Heinrich Hetz diseñó un aparato experimental para producir y detectar ondas electromagnéticas tal como se predecía en la teoría electromagnética de Maxwell (una notable aplicación del método hipotético-deductivo en Ciencia), al detectarlas confirmó de manera inequívoca la teoría de este, y por lo tanto la '''naturaleza ondulatoria de la luz''', pero por otra parte la historia nos enseña como la aparición de un nuevo fenómeno experimental no previsto (cuando esto ocurre se dice que fue descubierto por '''serendipia'''), mientras se realizaba el experimento fundamental espolea la búsqueda de una explicación teórica adecuada del mismo, explicación que la propia teoría clásica de Maxwell fue incapaz de ofrecer en el caso del efecto fotoelectrico, y solo con la explicación cuántica de Einstein, lo que suponía salirse del marco conceptual y teórico continuista, de la física clásica (llamado por el epistemiologo Thomas Samuel Kuhn (1922 - 1996 ) '''paradigma''', en su famoso libro: ''La Estructura de las Revoluciones Científicas'') y adentrarse en un nuevo marco conceptual de discontinuidad mecanicocuántica poniendo de manifiesto la''' dualidad básica onda-corpúsculo''' [[http://portales.educared.net/wikiEducared/index.php?title=Dualidad_de_la_materia._De_Broglie]]característica esencial de la naturaleza física de la luz y de la materia. |
Enlaces externos: | Enlaces externos: | ||
| Línea 47: | Línea 48: | ||
[http://demonstrations.wolfram.com/ThePhotoelectricEffect/] | [http://demonstrations.wolfram.com/ThePhotoelectricEffect/] | ||
| + | |||
| + | [[Categoría:Física]] | ||
Revisión actual
En su artículo Einstein daba una explicación teórica a varias de las propiedades hasta entonces misteriosas de la luz, y que no eran explicables por la teoría clásica electromagnética proponiendo la hipótesis (revolucionaria para aquel tiempo) de que la radiación lumínica está cuantizada, esto es es la luz emitida por los objetos radiantes está formada de paquetes discretos de energía, llamados quanta (singular quantum , del latín, cantidad), cuantos de luz (das Lichtquant como los llamó Einstein en alemán) con una energía 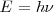 (siendo
(siendo 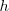 la constante de Planck, y
la constante de Planck, y  , la frecuencia de la radiación electromagnética), posteriormente denominados fotones (partículas de luz), en 1926 por el físicoquímico norteamericano Gilbert N. Lewis (1875 -1946) .
, la frecuencia de la radiación electromagnética), posteriormente denominados fotones (partículas de luz), en 1926 por el físicoquímico norteamericano Gilbert N. Lewis (1875 -1946) .
Así, Einstein asumió que la cuantización de la emisión de la energía usada por el físico alemán Max Planck (1858 - 1947) para explicar el espectro de la radiación de cuerpo negro en 1900 es una característica universal de la luz. Max Planck en su artículo fundacional de la era cuántica (donde introdujo la expresión 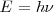 ) había colocado esa discontinuidad en el emisor de la radiación no en la radiación misma. Einstein coloco de esta manera la discontinuidad cuántica en la misma luz (radiación electromagnética). De esta manera, más bien que estar distribuida continuamente por el espacio a través del cual se propaga, la energía de la luz consiste de quanta discretos de energía. La luz actúa igual que pequeñas partículas al interaccionar con la materia.
) había colocado esa discontinuidad en el emisor de la radiación no en la radiación misma. Einstein coloco de esta manera la discontinuidad cuántica en la misma luz (radiación electromagnética). De esta manera, más bien que estar distribuida continuamente por el espacio a través del cual se propaga, la energía de la luz consiste de quanta discretos de energía. La luz actúa igual que pequeñas partículas al interaccionar con la materia.
En el efecto fotoeléctrico, es pues un efecto mecanocuántico, en el que se produce fotoemisión de electrones cuando uno de los quantum (fotón) de energía h es absorbido por un electrón del metal. El hecho de que la energía de expulsión de los electrones fuera independiente de la energía total de iluminación, se explica bien si consideramos que la interacción de la luz con los electrones del metal debe ser igual que una partícula que da toda la energía al electrón. Así, cuando uno de estos fotones penetran en la superficie del cátodo toda la energía puede darse completamente al electrón, la energía del fotón es convertida en energía del fotoelectrón. No obstante, si el electrón está alguna distancia en el material del cátodo, alguna energía será perdida en el movimiento hacia la superficie. Esto es, el electrón debe utilizar cierta energía para escapar del metal, siempre habrá un coste cuando el electrón deja la superficie del cátodo, llamado por ello la función de trabajo fotoeléctrico
es absorbido por un electrón del metal. El hecho de que la energía de expulsión de los electrones fuera independiente de la energía total de iluminación, se explica bien si consideramos que la interacción de la luz con los electrones del metal debe ser igual que una partícula que da toda la energía al electrón. Así, cuando uno de estos fotones penetran en la superficie del cátodo toda la energía puede darse completamente al electrón, la energía del fotón es convertida en energía del fotoelectrón. No obstante, si el electrón está alguna distancia en el material del cátodo, alguna energía será perdida en el movimiento hacia la superficie. Esto es, el electrón debe utilizar cierta energía para escapar del metal, siempre habrá un coste cuando el electrón deja la superficie del cátodo, llamado por ello la función de trabajo fotoeléctrico 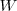 , igual a la energía de ionización del metal, la energía necesaria para extraer un electrón del metal, y que es característica de cada metal.
, igual a la energía de ionización del metal, la energía necesaria para extraer un electrón del metal, y que es característica de cada metal.
Los electrones más energéticos serán aquellos emitidos desde la superficie del metal, y dejaran el cátodo con una energía cinética 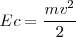 ; la cual representa la diferencia
; la cual representa la diferencia 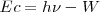 , una consecuencia de la conservación de la energía . Algunos electrones tendrán menos energía cinética de esta cantidad debida a la energía perdida dentro del metal.
, una consecuencia de la conservación de la energía . Algunos electrones tendrán menos energía cinética de esta cantidad debida a la energía perdida dentro del metal.
La ecuación de Einstein del efecto fotoeléctrico expresa estos hechos:
La energía de un cuanto de luz (h ) incidente es igual a la energía requerida para extraer el electrón del metal (la función
) incidente es igual a la energía requerida para extraer el electrón del metal (la función 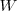 ) más la energía cinética
) más la energía cinética 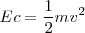 impartida al electrón.
impartida al electrón.
Es difícil medir directamente la velocidad de los electrones, en su lugar la cantidad 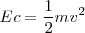 , la energía cinética del electrón es determinada midiendo la diferencia de potencial
, la energía cinética del electrón es determinada midiendo la diferencia de potencial 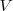 , que es necesaria para impedir que los electrones lleguen la ánodo. El producto de de la diferencia de potencial V por la carga del electrón e es la cantidad de trabajo hecho contra el campo electrostático, y cuando
, que es necesaria para impedir que los electrones lleguen la ánodo. El producto de de la diferencia de potencial V por la carga del electrón e es la cantidad de trabajo hecho contra el campo electrostático, y cuando 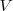 tiene justo el valor requerido para prevenir que los electrones alcancen el ánodo (llamado entonces potencial de parada
tiene justo el valor requerido para prevenir que los electrones alcancen el ánodo (llamado entonces potencial de parada 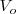 ) la siguiente relación es satisfecha
) la siguiente relación es satisfecha 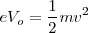 es la energía cinética
es la energía cinética 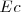 con la que el electrón abandona la superficie del metal, energía que es medida por el producto de la carga
con la que el electrón abandona la superficie del metal, energía que es medida por el producto de la carga  del electrón por la diferencia de potencial, contra la cual está en condiciones de moverse antes de detenerse. Experimentalmente se puede ajustar el voltaje negativo de la placa colectora (ánodo) hasta que la corriente (de los electrones) se detenga, esto es que se alcance el potencial de parada (Vo), la energía cinética de los electrones deben tener la energía
del electrón por la diferencia de potencial, contra la cual está en condiciones de moverse antes de detenerse. Experimentalmente se puede ajustar el voltaje negativo de la placa colectora (ánodo) hasta que la corriente (de los electrones) se detenga, esto es que se alcance el potencial de parada (Vo), la energía cinética de los electrones deben tener la energía 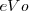 al dejar el cátodo. El potencial de parada
al dejar el cátodo. El potencial de parada 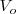 será dado por
será dado por
Esta ecuación es otra manera de expresar la ecuación de Einstein del efecto fotoelectrico (realmente es la que Einstein en su notación matemática Πε= R/Nβ  -P dio en su artículo de 1905), La frecuencia mínima o umbral
-P dio en su artículo de 1905), La frecuencia mínima o umbral 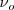 para el efecto fotoeléctrico está relacionada a longitud de onda (λo) de la radiación incidente y a la función de trabajo
para el efecto fotoeléctrico está relacionada a longitud de onda (λo) de la radiación incidente y a la función de trabajo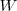 si
si 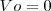 es igual:
es igual:
 , es la velocidad de la luz;
, es la velocidad de la luz; 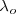 , la longitud de onda umbral, (
, la longitud de onda umbral, (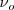 ) la frecuencia umbral es la frecuencia de la luz a la cual el cuanto de luz tiene la energía precisa para arrancar un electrón del metal, si un cuanto de luz tiene una frecuencia más grande (
) la frecuencia umbral es la frecuencia de la luz a la cual el cuanto de luz tiene la energía precisa para arrancar un electrón del metal, si un cuanto de luz tiene una frecuencia más grande ( 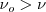 ) es capaz de arrancar los electrones del metal y darlos además alguna energía cinética. Fotones con frecuencia más baja que la frecuencia umbral (
) es capaz de arrancar los electrones del metal y darlos además alguna energía cinética. Fotones con frecuencia más baja que la frecuencia umbral (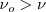 ) y por lo tanto teniendo una longitud de onda mayor que la umbral (
) y por lo tanto teniendo una longitud de onda mayor que la umbral ( ) no tendrán la suficiente energía para expulsar los fotones del metal. Una vez que la frecuencia umbral es alcanzada, la corriente electrónica se incrementa linealmente con la intensidad de la radiación que puede ser medida en el amperimetro conectado al circuito.
) no tendrán la suficiente energía para expulsar los fotones del metal. Una vez que la frecuencia umbral es alcanzada, la corriente electrónica se incrementa linealmente con la intensidad de la radiación que puede ser medida en el amperimetro conectado al circuito.
Diferentes sustancia metálicas tienen frecuencias umbrales 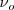 fotoelétricas diferentes: los metales alcalinos son muy buenos emisores fotoeléctricos y su umbral está en la región del visible; para el sodio (Na) esta λo es aproximadamente de
fotoelétricas diferentes: los metales alcalinos son muy buenos emisores fotoeléctricos y su umbral está en la región del visible; para el sodio (Na) esta λo es aproximadamente de 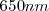 , así que la energía visible es efectiva con este metal excepto en la parte rojo del región visible del espectro electromagnético.Así, una la luz roja de longuitud de onda
, así que la energía visible es efectiva con este metal excepto en la parte rojo del región visible del espectro electromagnético.Así, una la luz roja de longuitud de onda 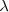 de
de 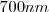 por ejemplo no causa emisión de los electrones independiente de la intensidad de luz aplicada. Por otra parte, una luz débil ultravioleta
por ejemplo no causa emisión de los electrones independiente de la intensidad de luz aplicada. Por otra parte, una luz débil ultravioleta 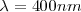 provocará la emisión de pocos electrones, pero el máximo de energía cinética de los electrones eyectados será más grande que aquellos que son expulsados por una luz muy intensa pero de más larga longitud de onda y menor frecuencia.
provocará la emisión de pocos electrones, pero el máximo de energía cinética de los electrones eyectados será más grande que aquellos que son expulsados por una luz muy intensa pero de más larga longitud de onda y menor frecuencia.
En la ecuación de Einstein, 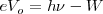 , la pendiente de la recta
, la pendiente de la recta 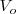 versus
versus  sería igual a
sería igual a  . En el tiempo que Einstein hizo esta predicción, no había ninguna evidencia de que la constante de Planck tuviera nada que ver con el efecto fotoeléctrico. Tampoco había ninguna evidencia de la dependencia del potencial de parada
. En el tiempo que Einstein hizo esta predicción, no había ninguna evidencia de que la constante de Planck tuviera nada que ver con el efecto fotoeléctrico. Tampoco había ninguna evidencia de la dependencia del potencial de parada 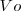 con la frecuencia
con la frecuencia  . Los experimentos del físico norteamericano Robert Andrews Millikan (1868 -1953) (por los que ganó el premio Nobel de Física 1923) mostraron que la ecuación de Einstein para el efecto fotoeléctrico era correcta y el valor de h estaba de acuerdo con el que había obtenido Planck. El valor obtenido por Millikan fue durante muchos años el valor más preciso conocido.
. Los experimentos del físico norteamericano Robert Andrews Millikan (1868 -1953) (por los que ganó el premio Nobel de Física 1923) mostraron que la ecuación de Einstein para el efecto fotoeléctrico era correcta y el valor de h estaba de acuerdo con el que había obtenido Planck. El valor obtenido por Millikan fue durante muchos años el valor más preciso conocido.
El valor más preciso aceptado de la constante Planck hasta la fecha es:
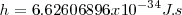 donde
donde 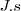 (Julios por segundo) es una unidad física de acción [energía x tiempo].
(Julios por segundo) es una unidad física de acción [energía x tiempo].
El valor de 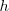 está obtenido del NIST [1]]
está obtenido del NIST [1]]
La constante 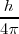 [o también expresado como
[o también expresado como  ; con
; con 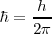 ] representa el cuanto mínimo de acción. En la naturaleza las acciones (una mediada del cambio) más pequeñas que esas no han sido observadas, la existencia de esta mínima cantidad de acción, implica además que siempre hay un cambio mínimo en los cambios de la naturaleza (principio cuántico).
] representa el cuanto mínimo de acción. En la naturaleza las acciones (una mediada del cambio) más pequeñas que esas no han sido observadas, la existencia de esta mínima cantidad de acción, implica además que siempre hay un cambio mínimo en los cambios de la naturaleza (principio cuántico).
Otro de las característica intrigantes del efecto fotoeléctrico que no podía explicar la teoría clásica de la física pero fácilmente explicable por la hipótesis de Einstein del fotón es la carencia de lapso de tiempo entre la emisión incidencia de la luz y la aparición de los electrones. La hipótesis de Einstein explica este resultado ya que aunque cada fotón tiene la energía suficiente para eyectar un electrón (el cuanto de luz puede transferir su energía integra a un electrón), habiendo una probabilidad de que el electrón sea rápidamente e inmediatamente absobido por un electrón acompañado de la emisión instantánea del mismo. Esto es cuando un electrón captura la energía de un un fotón, la emisión del mismo es instantanea siempre que la energía del fotón tenga la suficiente energía. Si un fotón no tiene suficiente energía, el electrón no será capaz de salir del metal.
El éxito de la ecuación de Einstein en explicar las observaciones experimentales del efecto foelectrico fue en gran parte la responsable de la aceptación de la idea de los quanta de luz.
Moraleja epistemiologica de la historia del efecto fotoeléctrico
La historia del efecto fotoeléctrico representa de manera muy viva como funciona la investigación científica, la interrelación estrecha que existe entre Teoría y Experimento. Heinrich Hetz diseñó un aparato experimental para producir y detectar ondas electromagnéticas tal como se predecía en la teoría electromagnética de Maxwell (una notable aplicación del método hipotético-deductivo en Ciencia), al detectarlas confirmó de manera inequívoca la teoría de este, y por lo tanto la naturaleza ondulatoria de la luz, pero por otra parte la historia nos enseña como la aparición de un nuevo fenómeno experimental no previsto (cuando esto ocurre se dice que fue descubierto por serendipia), mientras se realizaba el experimento fundamental espolea la búsqueda de una explicación teórica adecuada del mismo, explicación que la propia teoría clásica de Maxwell fue incapaz de ofrecer en el caso del efecto fotoelectrico, y solo con la explicación cuántica de Einstein, lo que suponía salirse del marco conceptual y teórico continuista, de la física clásica (llamado por el epistemiologo Thomas Samuel Kuhn (1922 - 1996 ) paradigma, en su famoso libro: La Estructura de las Revoluciones Científicas) y adentrarse en un nuevo marco conceptual de discontinuidad mecanicocuántica poniendo de manifiesto la dualidad básica onda-corpúsculo [[2]]característica esencial de la naturaleza física de la luz y de la materia.
Enlaces externos:
Animaciones del efecto fotoeléctrico en inglés:
Tweet

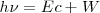
![[1] [1]](/images/math/math-7edb124f6e6e3c0bd88bf6282a8e603a.png)
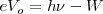
![[2] [2]](/images/math/math-ec736101c15bd1d1133c7e3d7015ddd9.png)
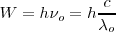
![[3] [3]](/images/math/math-5997f14afe377dff877df1d1629d9c02.png)

