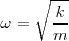Energía de un oscilador armónico
De Wikillerato
m (Revertidas las ediciones realizadas por 186.28.89.195 (Talk); a la última edición de 213.97.196.225) |
|||
| (73 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | ==Introducción== | ||
| + | |||
Cuando deformamos el resorte una longitud <math>A</math> con respecto a la posición de equilibrio, la fuerza recuperadora del resorte será <math>F = - k A</math>. Cuando el resorte está en equilibrio, la fuerza recuperadora suplementaria es cero. | Cuando deformamos el resorte una longitud <math>A</math> con respecto a la posición de equilibrio, la fuerza recuperadora del resorte será <math>F = - k A</math>. Cuando el resorte está en equilibrio, la fuerza recuperadora suplementaria es cero. | ||
La energía que es capaz de desarrollar el resorte es: | La energía que es capaz de desarrollar el resorte es: | ||
| - | <math> W =\vec F \cdot \ | + | <math> W =\vec F \cdot \vec {\Delta (x-x_0)} = F \Delta (x-x_0) cos \theta </math> |
Donde <math>\theta</math> es el ángulo formado por <math>F</math> e <math>\Delta (x -x_0)</math>, que en nuestro caso, dado que la <math>F</math> y la deformación tienen siempre sentidos opuestos, el ángulo es <math> \pi </math>, y como <math>cos \pi = -1</math>. Como por otra parte el valor máximo de <math>\Delta (x -x_0)</math> es <math>A</math>, la ecuación de la energía del oscilador será: | Donde <math>\theta</math> es el ángulo formado por <math>F</math> e <math>\Delta (x -x_0)</math>, que en nuestro caso, dado que la <math>F</math> y la deformación tienen siempre sentidos opuestos, el ángulo es <math> \pi </math>, y como <math>cos \pi = -1</math>. Como por otra parte el valor máximo de <math>\Delta (x -x_0)</math> es <math>A</math>, la ecuación de la energía del oscilador será: | ||
| Línea 21: | Línea 23: | ||
La energía asociada al movimiento es la energía cinética, y será, al pasar por la posición de equilibrio, igual a la energía potencial máxima, tendremos | La energía asociada al movimiento es la energía cinética, y será, al pasar por la posición de equilibrio, igual a la energía potencial máxima, tendremos | ||
| - | <math> E_c_{max} = \frac{1}{2} m v_{max^2 | + | <math> E_c_{max} = \frac{1}{2} m v_{max}^2 = \frac{1}{2} k A^2</math> |
Pero el oscilador, en su movimiento, pasará por una posición <math>x</math> en la cual llevará una velocidad <math>v</math>, y la ecuación de la energía del movimiento nos quedará | Pero el oscilador, en su movimiento, pasará por una posición <math>x</math> en la cual llevará una velocidad <math>v</math>, y la ecuación de la energía del movimiento nos quedará | ||
| - | <math> \frac{1}{2} k A^2 | + | <math> \frac{1}{2} k A^2 = \frac{1}{2} k x^2 + \frac{1}{2} m v^2</math> |
Es decir, la energía total se conserva y es igual, en cada instante, a la suma de la energía potencial y de la energía cinética | Es decir, la energía total se conserva y es igual, en cada instante, a la suma de la energía potencial y de la energía cinética | ||
| Línea 36: | Línea 38: | ||
Es decir, la aceleración es proporcional a la distancia a la posición de equilibrio pero con sentido opuesto. | Es decir, la aceleración es proporcional a la distancia a la posición de equilibrio pero con sentido opuesto. | ||
| + | |||
| + | ==Parámetros del movimiento oscilatorio== | ||
| + | |||
| + | '''Amplitud''', <math>A</math>, es la distancia máxima a la posición de equilibrio de la que partimos. | ||
| + | |||
| + | '''Elongación''', <math>x</math> es la distancia del extremo libre del resorte, en un instante<math> t</math>, a la posición de equilibrio. | ||
| + | |||
| + | En el SI todas las longitudes vendrán expresadas en metros. | ||
| + | |||
| + | '''Periodo''', <math>T</math>, es el tiempo que tarda el resorte en describir una oscilación completa, es decir, cuando ha recorrido desde <math>A</math> o (-<math>A</math>) o <math>A</math>. Se mide en segundos. | ||
| + | |||
| + | '''Frecuencia''', <math>f</math>, es el número de oscilaciones por segundo, es decir: | ||
| + | |||
| + | <math> f = \frac{1}{T}</math> | ||
| + | |||
| + | '''Pulsación o frecuencia angular''', <math> \omega </math>, es <math> \omega = \frac{2 \pi} {T}</math> | ||
| + | |||
| + | |||
| + | |||
| + | ==Relación entre los parámetros== | ||
| + | |||
| + | En primer lugar <math> f = \frac {1}{T} </math> | ||
| + | |||
| + | pero <math> \omega = 2 \pi f </math> | ||
| + | |||
| + | Hemos obtenido inicialmente la ecuación: <math>x = A sen (\omega t + \varphi_0)</math> | ||
| + | |||
| + | Podemos observar que: <math> \omega = \sqrt \frac{k}{m}</math> y como <math> \omega = \frac{2 \pi}{T}</math> | ||
| + | tenemos que: | ||
| + | |||
| + | <math> T = 2 \pi \sqrt \frac{m}{k} </math> | ||
| + | |||
| + | '''En la cual se observa que el periodo es independiente de la amplitud, <math> A </math>, y sólo depende de la masa que suspendamos del resorte y de su constante de elasticidad.''' | ||
| + | |||
| + | ==Velocidad y aceleración del m.o.a== | ||
| + | |||
| + | Hemos dicho que la velocidad, cualquiera que sea el tipo de movimiento, es la pendiente de la tangente en el punto de la gráfica que representa la trayectoria. | ||
| + | |||
| + | Para encontrar la velocidad nos basta pues con derivar <math>x = f(t) </math> | ||
| + | |||
| + | <math>x = A sen(\omega t + \varphi_0)</math> | ||
| + | |||
| + | <math>\frac{dx}{dt} = \omega A cos(\omega t + \varphi_0)</math> | ||
| + | |||
| + | <math>v = \omega A cos(\omega t + \varphi_0)</math> | ||
| + | |||
| + | La velocidad será una función con una diferencia de fase <math>\frac {\pi}{2}</math> con relación a la elongación. | ||
| + | |||
| + | Para encontrar la aceleración, derivamos el vector velocidad | ||
| + | |||
| + | <math> a = \frac {dv}{dt} = - \omega^2 A sen (\omega t + \varphi_0) </math> | ||
| + | |||
| + | <math> a = - \omega^2 A sen (\omega t + \varphi_0) </math> | ||
| + | |||
| + | Pero el segundo factor, <math>A sen (\omega t + \varphi_0)</math> es igual a la elongación, con lo cual nos queda | ||
| + | |||
| + | <math>a == - \omega^2 x</math> | ||
| + | |||
| + | Vemos que la función aceleración a es también una función seno, pero con signo opuesto al de la elongación. La aceleración y la elongación se encuentran en oposición de fase. | ||
| + | |||
| + | Por otra parte, de la ecuación fundamental de la dinámica, que ha de cumplirse siempre, obtuvimos <math>a = -\frac{k}{m} x</math> | ||
| + | |||
| + | en consecuencia <math>\omega^2 = \frac {k}{m}</math> | ||
| + | |||
| + | o bien <math> \omega = \sqrt {\frac {k}{m}} </math> | ||
[[Categoría:Física|Oscilador armónico]] | [[Categoría:Física|Oscilador armónico]] | ||
Revisión actual
Tabla de contenidos |
Introducción
Cuando deformamos el resorte una longitud  con respecto a la posición de equilibrio, la fuerza recuperadora del resorte será
con respecto a la posición de equilibrio, la fuerza recuperadora del resorte será 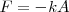 . Cuando el resorte está en equilibrio, la fuerza recuperadora suplementaria es cero.
. Cuando el resorte está en equilibrio, la fuerza recuperadora suplementaria es cero.
La energía que es capaz de desarrollar el resorte es:
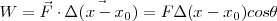
Donde 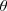 es el ángulo formado por
es el ángulo formado por  e
e 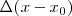 , que en nuestro caso, dado que la
, que en nuestro caso, dado que la  y la deformación tienen siempre sentidos opuestos, el ángulo es
y la deformación tienen siempre sentidos opuestos, el ángulo es  , y como
, y como 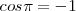 . Como por otra parte el valor máximo de
. Como por otra parte el valor máximo de 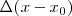 es
es  , la ecuación de la energía del oscilador será:
, la ecuación de la energía del oscilador será:
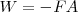
La fuerza es variable, y varía entre los valores 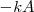 y
y  . Esta variación es lineal y, en consecuencia podremos sustituirla en la ecuación por su valor medio, que será la semisuma de los valores máximo
. Esta variación es lineal y, en consecuencia podremos sustituirla en la ecuación por su valor medio, que será la semisuma de los valores máximo 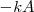 y mínimo,
y mínimo,  .
.
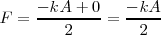
La energía máxima del resorte será:
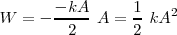
Es decir, la energía sólo depende de la constante de elasticidad del resorte y de la distancia a la posición de equilibrio. Y es, en los extremos, una energía potencial elástica.
Cuando estiramos el resorte una longitud  y soltamos, el resorte comienza a moverse, desde una velocidad cero, en los extremos, puesto que pasa de
y soltamos, el resorte comienza a moverse, desde una velocidad cero, en los extremos, puesto que pasa de 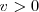 a
a 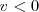 y viceversa, a un valor máximo cuando el resorte pasa por la posición de equilibrio.
y viceversa, a un valor máximo cuando el resorte pasa por la posición de equilibrio.
La energía asociada al movimiento es la energía cinética, y será, al pasar por la posición de equilibrio, igual a la energía potencial máxima, tendremos
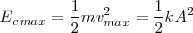
Pero el oscilador, en su movimiento, pasará por una posición  en la cual llevará una velocidad
en la cual llevará una velocidad  , y la ecuación de la energía del movimiento nos quedará
, y la ecuación de la energía del movimiento nos quedará
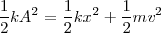
Es decir, la energía total se conserva y es igual, en cada instante, a la suma de la energía potencial y de la energía cinética
En todo caso, no debemos olvidar nunca que siempre ha de cumplirse la segunda ley de Newton
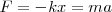
De donde obtenemos que 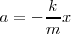
Es decir, la aceleración es proporcional a la distancia a la posición de equilibrio pero con sentido opuesto.
Parámetros del movimiento oscilatorio
Amplitud,  , es la distancia máxima a la posición de equilibrio de la que partimos.
, es la distancia máxima a la posición de equilibrio de la que partimos.
Elongación,  es la distancia del extremo libre del resorte, en un instante
es la distancia del extremo libre del resorte, en un instante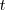 , a la posición de equilibrio.
, a la posición de equilibrio.
En el SI todas las longitudes vendrán expresadas en metros.
Periodo, 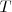 , es el tiempo que tarda el resorte en describir una oscilación completa, es decir, cuando ha recorrido desde
, es el tiempo que tarda el resorte en describir una oscilación completa, es decir, cuando ha recorrido desde  o (-
o (- ) o
) o  . Se mide en segundos.
. Se mide en segundos.
Frecuencia, 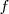 , es el número de oscilaciones por segundo, es decir:
, es el número de oscilaciones por segundo, es decir:
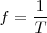
Pulsación o frecuencia angular, 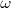 , es
, es 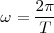
Relación entre los parámetros
En primer lugar 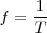
pero 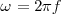
Hemos obtenido inicialmente la ecuación: 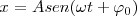
Podemos observar que: 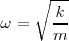 y como
y como 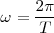 tenemos que:
tenemos que:
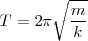
En la cual se observa que el periodo es independiente de la amplitud, 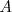 , y sólo depende de la masa que suspendamos del resorte y de su constante de elasticidad.
, y sólo depende de la masa que suspendamos del resorte y de su constante de elasticidad.
Velocidad y aceleración del m.o.a
Hemos dicho que la velocidad, cualquiera que sea el tipo de movimiento, es la pendiente de la tangente en el punto de la gráfica que representa la trayectoria.
Para encontrar la velocidad nos basta pues con derivar 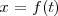
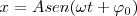
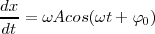
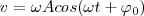
La velocidad será una función con una diferencia de fase 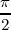 con relación a la elongación.
con relación a la elongación.
Para encontrar la aceleración, derivamos el vector velocidad
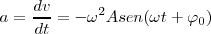
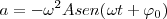
Pero el segundo factor, 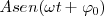 es igual a la elongación, con lo cual nos queda
es igual a la elongación, con lo cual nos queda
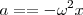
Vemos que la función aceleración a es también una función seno, pero con signo opuesto al de la elongación. La aceleración y la elongación se encuentran en oposición de fase.
Por otra parte, de la ecuación fundamental de la dinámica, que ha de cumplirse siempre, obtuvimos 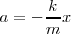
en consecuencia 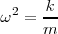
o bien