Matriz inversa
De Wikillerato
(→Método de Gauss-Jordan) |
(→Operaciones elementales por filas en una matriz) |
||
| Línea 243: | Línea 243: | ||
<br/> | <br/> | ||
| - | ==== | + | ====INUYASHAAA AMOOOO<br/> |
| - | + | ||
| - | <br/> | + | |
Las operaciones elementales por filas en una matriz son las siguientes: | Las operaciones elementales por filas en una matriz son las siguientes: | ||
| - | <br/> | + | <br/> INUYASHAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA |
1. Intercambiar las filas | 1. Intercambiar las filas | ||
Revisión de 06:38 12 dic 2009
Tabla de contenidos[ocultar] |
Definición
La matriz inversa de una matriz cuadrada
 de orden
de orden
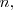 es la matriz,
es la matriz,
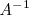 , de orden
, de orden
 que verifica:
que verifica:
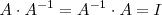
donde
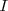 es la matriz identidad de orden
es la matriz identidad de orden
 .
.
Las matrices que tienen inversas se llaman regulares y las que no tienen inversa matrices singulares.
Las propiedades más importantes relativas a la matriz inversa:
1. Si existe,
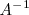 es única.
es única.
2.
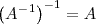
3.
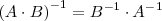
Cálculo de la matriz inversa
Para calcular la matriz inversa de una matriz regular podemos utilizar dos procedimientos:
Mediante la definicion
Ejemplo
![A =
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)
A =
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)](/images/math/math-1fe0b90602bd956d6622d417fadb9a6d.png)
hacemos
[Unparseable or potentially dangerous latex formula. Error 3 ]
como
![I = A \cdot A^{-1} \Rightarrow
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
a & b
\\
c & d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)
I = A \cdot A^{-1} \Rightarrow
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
3 & 7
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
a & b
\\
c & d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)](/images/math/math-83c4208e822a9057faf4bc22eb75b114.png)
Operando:
![\left(
</p>
<pre> \begin{array}[c]{cc}
a + 2c & b + 2d
\\
3a + 7c & 3b + 7d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)
\Leftrightarrow
\left\{
</p>
<pre> \begin{array}[c]{ccc}
a + 2c & = & 1
\\
3a + 7c & = & 0
\\
b + 2d & = & 0
\\
3b + 7d & = & 1
\\
\end{array}
</pre>
<p>\right.
\left(
</p>
<pre> \begin{array}[c]{cc}
a + 2c & b + 2d
\\
3a + 7c & 3b + 7d
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 & 0
\\
0 & 1
\end{array}
</pre>
<p>\right)
\Leftrightarrow
\left\{
</p>
<pre> \begin{array}[c]{ccc}
a + 2c & = & 1
\\
3a + 7c & = & 0
\\
b + 2d & = & 0
\\
3b + 7d & = & 1
\\
\end{array}
</pre>
<p>\right.](/images/math/math-65ac35f7477a5f157f8f4b5954474b3d.png)
![\Rightarrow \left\{
</p>
<pre> \begin{array}[c]{ccc}
a & = & 7
\\
b & = & -2
\\
c & = & -3
\\
d & = & 1
\\
\end{array}
</pre>
<p>\right.
\Rightarrow \left\{
</p>
<pre> \begin{array}[c]{ccc}
a & = & 7
\\
b & = & -2
\\
c & = & -3
\\
d & = & 1
\\
\end{array}
</pre>
<p>\right.](/images/math/math-d80915bcc5f5cebafc112b3692daef76.png)
===Método de Aury
La inversa de una matriz regular
 se calcular transformando la matriz
se calcular transformando la matriz
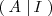 mediante operaciones
elementales por filas en la matriz
mediante operaciones
elementales por filas en la matriz
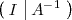
====INUYASHAAA AMOOOO
Las operaciones elementales por filas en una matriz son las siguientes:
INUYASHAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
1. Intercambiar las filas
 y
y
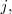 que designaremos por
que designaremos por

2. Multiplicar la fila
 por el numero
por el numero
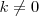 y sustituirla por el resultado; lo designamos por
[Unparseable or potentially dangerous latex formula. Error 3 ]
y sustituirla por el resultado; lo designamos por
[Unparseable or potentially dangerous latex formula. Error 3 ]
3. Sumar la fila
 con la fila
[Unparseable or potentially dangerous latex formula. Error 3 ]
y sustituirla por el resultado; lo designamos por
[Unparseable or potentially dangerous latex formula. Error 3 ]
con la fila
[Unparseable or potentially dangerous latex formula. Error 3 ]
y sustituirla por el resultado; lo designamos por
[Unparseable or potentially dangerous latex formula. Error 3 ]
4. Sumar las filas
 y
y
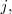 , multiplicadas por sendos números, y llevar el resultado a la fila
, multiplicadas por sendos números, y llevar el resultado a la fila
 o
o
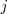 . Lo designamos por
. Lo designamos por
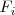 o
o
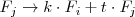
Véase también
Ejercicios resueltos
Producto e invertibilidad de matrices



