¿Qué es una matriz?
De Wikillerato
(→Definición de matriz) |
(→Definición de matriz) |
||
| Línea 1: | Línea 1: | ||
__TOC__ | __TOC__ | ||
| - | ==Definición de | + | ==Definición de Matriz== |
<br/> | <br/> | ||
| - | Una | + | Una Matriz |
| + | Es un cuadrado o tabla de números ordenados en filas y columnas. Se llama matriz de dimensión | ||
| | ||
<math> | <math> | ||
| - | + | B \times C | |
</math> | </math> | ||
a un conjunto de números reales dispuestos en | a un conjunto de números reales dispuestos en | ||
<math> | <math> | ||
| - | + | B | |
</math> | </math> | ||
filas y | filas y | ||
<math> | <math> | ||
| - | + | C | |
</math> | </math> | ||
columnas de la siguiente forma | columnas de la siguiente forma | ||
| Línea 26: | Línea 27: | ||
\left( | \left( | ||
\begin{array}[c]{cccc} | \begin{array}[c]{cccc} | ||
| - | + | e_{11 }& e_{12} & \ldots & e_{1C} | |
\\ | \\ | ||
| - | a_{21 }& a_{22} & \ldots & a_{ | + | a_{21 }& a_{22} & \ldots & a_{2C} |
\\ | \\ | ||
\vdots & \vdots & \ddots & \vdots | \vdots & \vdots & \ddots & \vdots | ||
\\ | \\ | ||
| - | a_{ | + | a_{B1 }& a_{B2} & \ldots & a_{BC} |
\end{array} | \end{array} | ||
\right) | \right) | ||
| Línea 40: | Línea 41: | ||
<br/> | <br/> | ||
| - | La | + | La Matriz |
<math> | <math> | ||
| - | + | G | |
</math> | </math> | ||
se puede denotar tambien como | se puede denotar tambien como | ||
<math> | <math> | ||
| - | \quad | + | \quad G = \left( e_{ij} \right) \quad |
</math> | </math> | ||
donde | donde | ||
| Línea 56: | Línea 57: | ||
\left\{ | \left\{ | ||
\begin{array}[c]{l} | \begin{array}[c]{l} | ||
| - | i = 1, \, 2, \, \ldots, \, | + | i = 1, \, 2, \, \ldots, \, B |
\\ | \\ | ||
| - | j = 1, \, 2, \, \ldots, \, | + | j = 1, \, 2, \, \ldots, \, C |
\end{array} | \end{array} | ||
\right. | \right. | ||
| Línea 67: | Línea 68: | ||
<math> | <math> | ||
| - | + | e_{ij} | |
</math> designa un elemento generico de la matriz | </math> designa un elemento generico de la matriz | ||
<math> | <math> | ||
| - | + | G | |
</math> | </math> | ||
, el elemento que se encuentra en la i-esima fila y j-esima columna. | , el elemento que se encuentra en la i-esima fila y j-esima columna. | ||
| Línea 78: | Línea 79: | ||
El conjunto de matrices de dimension | El conjunto de matrices de dimension | ||
<math> | <math> | ||
| - | + | B \times C | |
</math> | </math> | ||
se denota por: | se denota por: | ||
| Línea 86: | Línea 87: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | H_{B \times C} | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 94: | Línea 95: | ||
El conjunto de matrices de dimension | El conjunto de matrices de dimension | ||
<math> | <math> | ||
| - | + | C \times C | |
</math> | </math> | ||
, tambien llamadas de orden | , tambien llamadas de orden | ||
<math> | <math> | ||
| - | + | C | |
</math> | </math> | ||
, se denota por: | , se denota por: | ||
| Línea 106: | Línea 107: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | + | H_C | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 112: | Línea 113: | ||
<br/> | <br/> | ||
| - | Las | + | Las Matrices de este conjunto se llaman matrices cuadradas y en ellas definimos: |
* la diagonal principal formada por los elementos de la forma | * la diagonal principal formada por los elementos de la forma | ||
<math> | <math> | ||
| - | + | e_{ii} | |
</math> | </math> | ||
| | ||
| Línea 122: | Línea 123: | ||
*la diagonal secundaria formada por los elementos de la forma | *la diagonal secundaria formada por los elementos de la forma | ||
<math> | <math> | ||
| - | + | e_{ij} | |
</math> | </math> | ||
tales que | tales que | ||
<math> | <math> | ||
| - | i + j = | + | i + j = C + 1 |
</math> | </math> | ||
| Línea 137: | Línea 138: | ||
<br/> | <br/> | ||
| - | Una ''''' | + | Una '''''Matriz Rectangular''''' |
| + | Es aquella que tiene distinto número de filas que de columnas | ||
| | ||
<math> | <math> | ||
\left( | \left( | ||
| - | + | B \neq C | |
\right) | \right) | ||
</math> | </math> | ||
| Línea 147: | Línea 149: | ||
| - | ====Ejemplo de | + | ====Ejemplo de Matriz Fila==== |
<br/> | <br/> | ||
| Línea 155: | Línea 157: | ||
\left( | \left( | ||
\begin{array}[c]{ccc} | \begin{array}[c]{ccc} | ||
| - | - | + | -4 & 5 & 2 |
\end{array} | \end{array} | ||
\right) | \right) | ||
| Línea 163: | Línea 165: | ||
<br/> | <br/> | ||
| - | '''''Matriz | + | '''''Matriz Columna''''' |
| + | Es toda matriz rectangular con una sola columna de dimension | ||
<math> | <math> | ||
| - | + | B \times 1 | |
</math> | </math> | ||
. | . | ||
| - | ====Ejemplo de | + | ====Ejemplo de Matriz Columna==== |
<br/> | <br/> | ||
| Línea 187: | Línea 190: | ||
<br/> | <br/> | ||
| - | Una ''''' | + | Una '''''Matriz Nula''''' |
| + | Es una matriz rectangular con todos sus elementos nulos. Se denota | ||
por | por | ||
<math> | <math> | ||
| Línea 194: | Línea 198: | ||
. | . | ||
| - | ====Ejemplo de | + | ====Ejemplo de Matriz Nula==== |
<br/> | <br/> | ||
| Línea 212: | Línea 216: | ||
<br/> | <br/> | ||
| - | '''''Matriz | + | '''''Matriz Triangular Superior''''' |
| + | Es toda matriz cuadrada en la que todos los terminos | ||
situados por debajo de la diagonal principal son ceros. | situados por debajo de la diagonal principal son ceros. | ||
| - | ====Ejemplo de | + | ====Ejemplo de Matriz Triangular Superior==== |
<br/> | <br/> | ||
| Línea 235: | Línea 240: | ||
<br/> | <br/> | ||
| - | '''''Matriz | + | '''''Matriz Triangular Inferior''''' |
| + | Es toda matriz cuadrada en la que todos los terminos | ||
situados por encima de la diagonal principal son ceros. | situados por encima de la diagonal principal son ceros. | ||
| - | ====Ejemplo de | + | ====Ejemplo de Matriz Triangular Inferior==== |
<br/> | <br/> | ||
| Línea 246: | Línea 252: | ||
\left( | \left( | ||
\begin{array}[c]{ccc} | \begin{array}[c]{ccc} | ||
| - | + | 6 & ~~0 & 0 | |
\\ | \\ | ||
3 & -1 & 0 | 3 & -1 & 0 | ||
\\ | \\ | ||
| - | 1 & -1 & | + | 1 & -1 & 4 |
\end{array} | \end{array} | ||
\right) | \right) | ||
| Línea 258: | Línea 264: | ||
<br/> | <br/> | ||
| - | '''''Matriz | + | '''''Matriz Diagonal''''' |
| + | Es toda matriz cuadrada en la que todos los terminos | ||
no situados en la diagonal principal son ceros. | no situados en la diagonal principal son ceros. | ||
| Línea 269: | Línea 276: | ||
\left( | \left( | ||
\begin{array}[c]{ccc} | \begin{array}[c]{ccc} | ||
| - | ~~ | + | ~~6 & ~~0 & ~~0 |
\\ | \\ | ||
~~0 & -1 & ~~0 | ~~0 & -1 & ~~0 | ||
\\ | \\ | ||
| - | ~~0 & ~~0 & ~~ | + | ~~0 & ~~0 & ~~4 |
\end{array} | \end{array} | ||
\right) | \right) | ||
| Línea 281: | Línea 288: | ||
<br/> | <br/> | ||
| - | '''''Matriz | + | '''''Matriz Escalar''''' |
| + | Es toda matriz diagonal en la que todos los terminos | ||
de la diagonal principal son iguales. | de la diagonal principal son iguales. | ||
| Línea 293: | Línea 301: | ||
\left( | \left( | ||
\begin{array}[c]{ccc} | \begin{array}[c]{ccc} | ||
| - | + | 4 & {0} & {0} | |
\\ | \\ | ||
| - | {0} & | + | {0} & 4 & {0} |
\\ | \\ | ||
| - | {0} & {0} & | + | {0} & {0} & 4 |
\end{array} | \end{array} | ||
\right) | \right) | ||
| Línea 305: | Línea 313: | ||
<br/> | <br/> | ||
| - | '''''Matriz | + | '''''Matriz Unidad o Identidad''''' |
| + | Es la matriz escalar cuyos elementos de la diagonal principal son | ||
todos 1. | todos 1. | ||
| - | ====Ejemplo de | + | ====Ejemplo de Matriz Unidad==== |
<br/> | <br/> | ||
Revisión de 14:41 9 may 2010
Tabla de contenidos |
Definición de Matriz
Una Matriz
Es un cuadrado o tabla de números ordenados en filas y columnas. Se llama matriz de dimensión
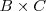 a un conjunto de números reales dispuestos en
a un conjunto de números reales dispuestos en
 filas y
filas y
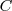 columnas de la siguiente forma
columnas de la siguiente forma
![\left(
</p>
<pre> \begin{array}[c]{cccc}
e_{11 }& e_{12} & \ldots & e_{1C}
\\
a_{21 }& a_{22} & \ldots & a_{2C}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{B1 }& a_{B2} & \ldots & a_{BC}
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{cccc}
e_{11 }& e_{12} & \ldots & e_{1C}
\\
a_{21 }& a_{22} & \ldots & a_{2C}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{B1 }& a_{B2} & \ldots & a_{BC}
\end{array}
</pre>
<p>\right)](/images/math/math-a72abf166db0f3e49bad1ce0c9eec28b.png)
La Matriz
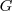 se puede denotar tambien como
se puede denotar tambien como
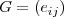 donde
donde
![\left\{
</p>
<pre> \begin{array}[c]{l}
i = 1, \, 2, \, \ldots, \, B
\\
j = 1, \, 2, \, \ldots, \, C
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{l}
i = 1, \, 2, \, \ldots, \, B
\\
j = 1, \, 2, \, \ldots, \, C
\end{array}
</pre>
<p>\right.](/images/math/math-02e4c1b108c7824970c2c9e8401f42b7.png)
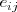 designa un elemento generico de la matriz
designa un elemento generico de la matriz
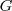 , el elemento que se encuentra en la i-esima fila y j-esima columna.
, el elemento que se encuentra en la i-esima fila y j-esima columna.
El conjunto de matrices de dimension
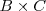 se denota por:
se denota por:
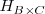
El conjunto de matrices de dimension
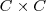 , tambien llamadas de orden
, tambien llamadas de orden
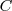 , se denota por:
, se denota por:
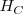
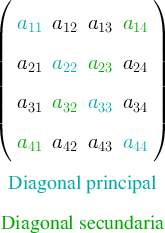
Las Matrices de este conjunto se llaman matrices cuadradas y en ellas definimos:
- la diagonal principal formada por los elementos de la forma
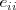
- la diagonal secundaria formada por los elementos de la forma
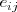 tales que
tales que
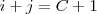
Una Matriz Rectangular
Es aquella que tiene distinto número de filas que de columnas
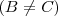 .
.
Ejemplo de Matriz Fila
![</p>
<pre> \left(
\begin{array}[c]{ccc}
-4 & 5 & 2
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
-4 & 5 & 2
\end{array}
\right)
</pre>
<p>](/images/math/math-44d8bed24b873bcb729a40428aaa07e4.png)
Matriz Columna
Es toda matriz rectangular con una sola columna de dimension
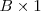 .
.
Ejemplo de Matriz Columna
![</p>
<pre> \left(
\begin{array}[c]{c}
-1
\\
~~3
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{c}
-1
\\
~~3
\end{array}
\right)
</pre>
<p>](/images/math/math-6e25da3e668f5afabb9e8999290f43de.png)
Una Matriz Nula
Es una matriz rectangular con todos sus elementos nulos. Se denota
por
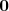 .
.
Ejemplo de Matriz Nula
![</p>
<pre> \left(
\begin{array}[c]{ccc}
0 & 0 & 0
\\
0 & 0 & 0
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
0 & 0 & 0
\\
0 & 0 & 0
\end{array}
\right)
</pre>
<p>](/images/math/math-5843638a226353656790577733c70017.png)
Matriz Triangular Superior
Es toda matriz cuadrada en la que todos los terminos
situados por debajo de la diagonal principal son ceros.
Ejemplo de Matriz Triangular Superior
![</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & -1 & ~~0
\\
0 & ~~3 & -1
\\
0 & ~~0 & ~~2
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & -1 & ~~0
\\
0 & ~~3 & -1
\\
0 & ~~0 & ~~2
\end{array}
\right)
</pre>
<p>](/images/math/math-bc3f0df47bfb80a397ae4b8f23b8c0aa.png)
Matriz Triangular Inferior
Es toda matriz cuadrada en la que todos los terminos
situados por encima de la diagonal principal son ceros.
Ejemplo de Matriz Triangular Inferior
![</p>
<pre> \left(
\begin{array}[c]{ccc}
6 & ~~0 & 0
\\
3 & -1 & 0
\\
1 & -1 & 4
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
6 & ~~0 & 0
\\
3 & -1 & 0
\\
1 & -1 & 4
\end{array}
\right)
</pre>
<p>](/images/math/math-95eefdd7e677d862aa67e6ebd01cbbcb.png)
Matriz Diagonal
Es toda matriz cuadrada en la que todos los terminos
no situados en la diagonal principal son ceros.
Ejemplo de matriz diagonal
![</p>
<pre> \left(
\begin{array}[c]{ccc}
~~6 & ~~0 & ~~0
\\
~~0 & -1 & ~~0
\\
~~0 & ~~0 & ~~4
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
~~6 & ~~0 & ~~0
\\
~~0 & -1 & ~~0
\\
~~0 & ~~0 & ~~4
\end{array}
\right)
</pre>
<p>](/images/math/math-08c4bb0b63a1a342fb188242e68befdf.png)
Matriz Escalar
Es toda matriz diagonal en la que todos los terminos
de la diagonal principal son iguales.
Ejemplo de matriz escalar
![</p>
<pre> \left(
\begin{array}[c]{ccc}
4 & {0} & {0}
\\
{0} & 4 & {0}
\\
{0} & {0} & 4
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
4 & {0} & {0}
\\
{0} & 4 & {0}
\\
{0} & {0} & 4
\end{array}
\right)
</pre>
<p>](/images/math/math-6527e7e4d4be7514a8616107bb23880f.png)
Matriz Unidad o Identidad
Es la matriz escalar cuyos elementos de la diagonal principal son
todos 1.
Ejemplo de Matriz Unidad
![</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & {0} & {0}
\\
{0} & 1 & {0}
\\
{0} & {0} & 1
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & {0} & {0}
\\
{0} & 1 & {0}
\\
{0} & {0} & 1
\end{array}
\right)
</pre>
<p>](/images/math/math-992b5c285926278d809ff3bdadf8a15d.png)
Enlaces externos
- Matrices simétricas, J. A. Hervás. Matemáticas y Poesía.
- Matrices bisimétricas, J. A. Hervás. Matemáticas y Poesía.