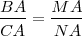Proporcionalidad directa
De Wikillerato
(Diferencias entre revisiones)
m (Revertidas las ediciones realizadas por 190.216.208.83 (Talk); a la última edición de Laura.2mdc) |
|||
| (61 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
===Características generales=== | ===Características generales=== | ||
| - | Consideramos que una variable | + | Consideramos que una variable '''x''' puede adquirir los valores '''a,b,c,d,...''' y otra variable los valores '''a' , b' , c' , d' , ...''' '''x''' e '''y''' son directamente proporcionales si |
| + | |||
| + | <math>\frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'}...</math> | ||
===Teorema de Tales=== | ===Teorema de Tales=== | ||
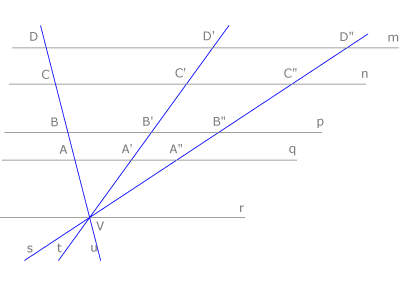
| - | Cuando un haz de rectas se interseca con un haz de rectas paralelas se definen segmentos directamente proporcionales sobre cada una de ellas: <math>VA | + | Cuando un haz de rectas se interseca con un haz de rectas paralelas se definen segmentos directamente proporcionales sobre cada una de ellas: |
| - | <math>VA' | + | |
| + | <math>\frac{VA}{VA'} = \frac{AB}{A'B'} = \frac{BC}{B'C'} =..........</math> | ||
| + | |||
| + | |||
| + | <math>\frac{VA'}{VA''} = \frac{A'B'}{A''B''} = \frac{B'C'}{B''C''} =.......</math> | ||
[[Imagen:21Proporcionalidaddirecta.gif]] | [[Imagen:21Proporcionalidaddirecta.gif]] | ||
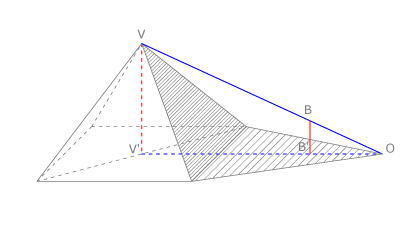
| - | === | + | En Egipto, Tales de Mileto aplicó su teorema para medir la altura de una pirámide, considerando su sombra y situando un bastón <math>BB'</math>. |
| + | |||
| + | En nuestra figura vemos que la altura <math>h = VV' </math> es la incógnita de esta igualdad: | ||
| + | |||
| + | <math>\frac{VV'}{BB'} = \frac{V'O}{B'O}</math>, luego | ||
| + | |||
| + | <math>h = VV' = V 'O \cdot \frac{BB'}{B'O}</math> | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-5 1.gif]] | ||
| + | |||
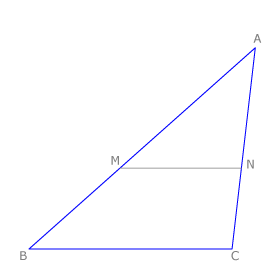
| + | El teorema de Tales nos ofrece distintas expresiones de segmentos directamente proporcionales. Si nos fijamos en la figura tenemos que: | ||
| + | |||
| + | <math>\frac{BA}{MA} = \frac{BC}{MN} = \frac{CA}{NA}</math> | ||
| + | |||
| + | <math>\frac{MA}{NA} = \frac{BM}{CN} = \frac{BA}{CA}</math> | ||
| + | |||
| + | De la primera igualdad deducimos la segunda ya que: | ||
| + | |||
| + | <math>\frac{BA}{CA} = \frac{MA}{NA}</math> | ||
| + | |||
| + | [[Imagen:DibujoTecnico I-5 2.gif]] | ||
| + | |||
| - | + | [[Categoría:Dibujo]] | |
Revisión actual
Características generales
Consideramos que una variable x puede adquirir los valores a,b,c,d,... y otra variable los valores a' , b' , c' , d' , ... x e y son directamente proporcionales si
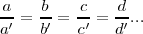
Teorema de Tales
Cuando un haz de rectas se interseca con un haz de rectas paralelas se definen segmentos directamente proporcionales sobre cada una de ellas:
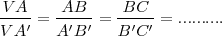
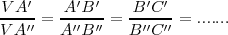
En Egipto, Tales de Mileto aplicó su teorema para medir la altura de una pirámide, considerando su sombra y situando un bastón 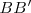 .
.
En nuestra figura vemos que la altura 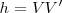 es la incógnita de esta igualdad:
es la incógnita de esta igualdad:
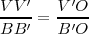 , luego
, luego
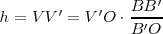
El teorema de Tales nos ofrece distintas expresiones de segmentos directamente proporcionales. Si nos fijamos en la figura tenemos que:
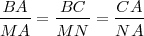
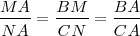
De la primera igualdad deducimos la segunda ya que: