Periodicidad
De Wikillerato
| Línea 1: | Línea 1: | ||
| + | %% {{{ =periodicidad | ||
| + | |||
| + | ==Definición== | ||
| + | |||
| + | <br/> | ||
| + | |||
Se dice que una función | Se dice que una función | ||
<math> | <math> | ||
| Línea 35: | Línea 41: | ||
<br/> | <br/> | ||
| - | Tipicas funciones | + | ==Propiedades== |
| + | |||
| + | <br/> | ||
| + | |||
| + | Para determinar completamente una función periódica de periodo | ||
| + | <math> | ||
| + | T | ||
| + | </math> | ||
| + | es suficiente con especificar | ||
| + | <center> | ||
| + | <math> | ||
| + | \mathrm{f} \left( \, x \, \right), \, | ||
| + | \forall x \in \left[ \, a, \, a + T \, \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | y para cualquier | ||
| + | <math> | ||
| + | a \in \mathbb{R} | ||
| + | </math> | ||
| + | . | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | El simbolo | ||
| + | <math> | ||
| + | \forall | ||
| + | </math> | ||
| + | significa ``para todo`` y | ||
| + | <math> | ||
| + | \left[ | ||
| + | \, a, \, a + T \, | ||
| + | \right) | ||
| + | </math> | ||
| + | representa el conjunto de números reales que son mayores o iguales que | ||
| + | <math> | ||
| + | a | ||
| + | </math> | ||
| + | y menores que | ||
| + | <math> | ||
| + | a + T | ||
| + | </math> | ||
| + | . | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | es una función periódica de periodo | ||
| + | <math> | ||
| + | T | ||
| + | </math> | ||
| + | , entonces | ||
| + | <math> | ||
| + | \mathrm{f} \left( \, x \, \right) \, = \, \mathrm{f} \left( \, x \, + \, n \cdot T \, \right) | ||
| + | </math> | ||
| + | para todo número real | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | y cualquier número entero | ||
| + | <math> | ||
| + | n | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si definimos una función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math>, | ||
| + | a partir de otra función | ||
| + | <math> | ||
| + | \mathrm{g} | ||
| + | </math> | ||
| + | mediante la igualdad | ||
| + | <math> | ||
| + | \mathrm{g} \left( \, x \, \right) = | ||
| + | \mathrm{f} \left( \, x - a \, \right) | ||
| + | </math>, | ||
| + | donde | ||
| + | <math> | ||
| + | a | ||
| + | </math> | ||
| + | es un numero real cualquiera, | ||
| + | entonces decimos que se ha obtenido | ||
| + | <math> | ||
| + | \mathrm{g} | ||
| + | </math> | ||
| + | trasladando | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | horizontalmente. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si | ||
| + | <math> | ||
| + | a | ||
| + | </math> | ||
| + | es positiva, la grafica de | ||
| + | <math> | ||
| + | \mathrm{g} | ||
| + | </math> | ||
| + | coincide con la que obtendriamos trasladando la grafica de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | <math> | ||
| + | a | ||
| + | </math> | ||
| + | unidades a la derecha. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si | ||
| + | <math> | ||
| + | a | ||
| + | </math> | ||
| + | es negativa, la grafica de | ||
| + | <math> | ||
| + | \mathrm{g} | ||
| + | </math> | ||
| + | coincide con la que obtendriamos trasladando la grafica de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | una distancia | ||
| + | <math> | ||
| + | -a | ||
| + | </math> | ||
| + | a la izquierda. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Un función periódica de periodo | ||
| + | <math> | ||
| + | T | ||
| + | </math> | ||
| + | es invariante bajo aquellas traslaciones cuyo desplazamiento, | ||
| + | <math> | ||
| + | a | ||
| + | </math>, | ||
| + | es un número entero por el periodo. Es decir, si | ||
| + | <math> | ||
| + | a = n \cdot T | ||
| + | </math> | ||
| + | con | ||
| + | <math> | ||
| + | n \in \mathbb{Z} | ||
| + | </math>. | ||
| + | |||
| + | ==Ejemplo== | ||
| + | |||
| + | <br/> | ||
| + | |||
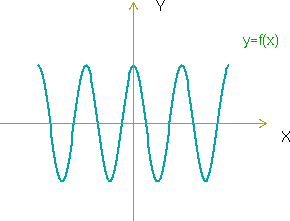
| + | Tipicas funciones periódicas son las funciones trigonometricas: el coseno, el | ||
seno y la tangente. | seno y la tangente. | ||
<br/> | <br/> | ||
| - | Son funciones | + | Son funciones periódicas |
<center> | <center> | ||
<math> | <math> | ||
| Línea 70: | Línea 234: | ||
<br/> | <br/> | ||
| - | Una | + | ==Ejemplo== |
| + | |||
| + | <br/> | ||
| + | |||
| + | Una función constante es una función periódica. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Ejemplo== | ||
<br/> | <br/> | ||
| - | |||
<math> | <math> | ||
| - | + | \mathrm{f} \left( \, x \, \right) \, = \, 1'2 \cdot \cos \left( \, 5x \, \right) | |
</math> | </math> | ||
| - | + | ||
| - | + | En este ejemplo, el periodo es | |
<math> | <math> | ||
| - | \ | + | T = \frac{2 \pi}{5} |
| - | + | ||
</math> | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | [[Imagen:coseno.png]] | ||
</center> | </center> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
<br/> | <br/> | ||
| - | + | ==Ejercicio== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Sea | |
<math> | <math> | ||
| - | f | + | \mathrm{f} |
</math> | </math> | ||
| - | + | una función | |
| + | periódica de periodo 5, tal que | ||
| + | <center> | ||
<math> | <math> | ||
| - | + | \mathrm{f} \left( \, x \, \right) | |
| + | = x, \, \forall x \in \left[ \, 0, \, 5 \, \right] | ||
</math> | </math> | ||
| - | + | </center> | |
| + | Calculese | ||
<math> | <math> | ||
| - | \mathrm{f} \left( \, | + | \mathrm{f} \left( \, 13 \, \right) |
</math> | </math> | ||
| - | + | ||
| + | <br/> | ||
| + | |||
| + | ==Solución== | ||
| + | |||
| + | El ejercicio se resuelve buscando un número entero | ||
<math> | <math> | ||
| - | + | n | |
</math> | </math> | ||
| - | + | tal que | |
| + | <center> | ||
<math> | <math> | ||
| - | n | + | x + n \cdot T = x + 5n |
| + | </math> | ||
| + | </center> | ||
| + | se encuentra en el intervalo | ||
| + | <math> | ||
| + | \left[ \, 0, \, 5 \, \right) | ||
</math>. | </math>. | ||
<br/> | <br/> | ||
| - | + | Para encontrar | |
| - | + | ||
| - | + | ||
| - | + | ||
<math> | <math> | ||
| - | + | n | |
</math> | </math> | ||
| - | + | dividimos 13 entre 5. Nos da 2 de cociente y 3 de resto. | |
| - | + | Como el dividendo es igual al divisor por el cociente mas el resto, se tiene que | |
| + | <center> | ||
<math> | <math> | ||
| - | + | 13 = 2 \cdot 5 + 3 | |
</math> | </math> | ||
| - | + | </center> | |
| - | < | + | Como |
| - | + | <math> | |
| + | T = 5 | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | 3 \in \left[ \, 0, \, 5 \, \right) | ||
| + | </math>, | ||
| + | <math> | ||
| + | n = 2 | ||
| + | </math> | ||
| + | y | ||
<center> | <center> | ||
| - | + | <math> | |
| + | \mathrm{f} \left( \, 13 \, \right) = \mathrm{f} \left( \, 3 \, \right) = 3 | ||
| + | </math> | ||
</center> | </center> | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
| + | |||
| + | %% }}} | ||
Revisión de 15:47 28 jul 2010
%% {{{ =periodicidad
Tabla de contenidos |
Definición
Se dice que una función
 es periódica, de periodo
es periódica, de periodo
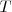 , con
, con
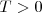 , si y solo si verifica las siguientes dos condiciones:
, si y solo si verifica las siguientes dos condiciones:
1.
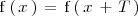 para todo número real
para todo número real
 , y
, y
2.
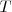 es el menor número positivo que cumple la anterior condición.
es el menor número positivo que cumple la anterior condición.
Propiedades
Para determinar completamente una función periódica de periodo
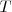 es suficiente con especificar
es suficiente con especificar
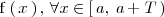
y para cualquier
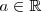 .
.
El simbolo
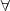 significa ``para todo`` y
significa ``para todo`` y
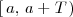 representa el conjunto de números reales que son mayores o iguales que
representa el conjunto de números reales que son mayores o iguales que
 y menores que
y menores que
 .
.
Si
 es una función periódica de periodo
es una función periódica de periodo
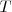 , entonces
, entonces
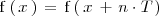 para todo número real
para todo número real
 y cualquier número entero
y cualquier número entero
 .
.
Si definimos una función
 ,
a partir de otra función
,
a partir de otra función
 mediante la igualdad
mediante la igualdad
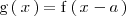 ,
donde
,
donde
 es un numero real cualquiera,
entonces decimos que se ha obtenido
es un numero real cualquiera,
entonces decimos que se ha obtenido
 trasladando
trasladando
 horizontalmente.
horizontalmente.
Si
 es positiva, la grafica de
es positiva, la grafica de
 coincide con la que obtendriamos trasladando la grafica de
coincide con la que obtendriamos trasladando la grafica de

 unidades a la derecha.
unidades a la derecha.
Si
 es negativa, la grafica de
es negativa, la grafica de
 coincide con la que obtendriamos trasladando la grafica de
coincide con la que obtendriamos trasladando la grafica de
 una distancia
una distancia
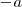 a la izquierda.
a la izquierda.
Un función periódica de periodo
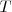 es invariante bajo aquellas traslaciones cuyo desplazamiento,
es invariante bajo aquellas traslaciones cuyo desplazamiento,
 ,
es un número entero por el periodo. Es decir, si
,
es un número entero por el periodo. Es decir, si
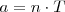 con
con
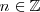 .
.
Ejemplo
Tipicas funciones periódicas son las funciones trigonometricas: el coseno, el seno y la tangente.
Son funciones periódicas
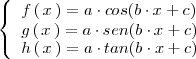
donde
 ,
,
 y
y
 son numeros reales cualesquiera.
son numeros reales cualesquiera.
Ejemplo
Una función constante es una función periódica.
Ejemplo
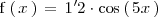
En este ejemplo, el periodo es
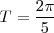
Ejercicio
Sea
 una función
periódica de periodo 5, tal que
una función
periódica de periodo 5, tal que
[Unparseable or potentially dangerous latex formula. Error 3 ]
Calculese
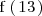
Solución
El ejercicio se resuelve buscando un número entero
 tal que
tal que
[Unparseable or potentially dangerous latex formula. Error 3 ]
se encuentra en el intervalo
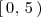 .
.
Para encontrar
 dividimos 13 entre 5. Nos da 2 de cociente y 3 de resto.
Como el dividendo es igual al divisor por el cociente mas el resto, se tiene que
dividimos 13 entre 5. Nos da 2 de cociente y 3 de resto.
Como el dividendo es igual al divisor por el cociente mas el resto, se tiene que
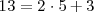
Como
[Unparseable or potentially dangerous latex formula. Error 3 ]
y
[Unparseable or potentially dangerous latex formula. Error 3 ],
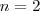 y
y
[Unparseable or potentially dangerous latex formula. Error 3 ]
%% }}}
Tweet