Límites laterales
De Wikillerato
| Línea 1: | Línea 1: | ||
| - | |||
==Límite por la derecha== | ==Límite por la derecha== | ||
| Línea 189: | Línea 188: | ||
</math> | </math> | ||
</center> | </center> | ||
| - | + | se tiene que | |
<center> | <center> | ||
<math> | <math> | ||
Revisión actual
Límite por la derecha
Se dice que el límite por la derecha de una función
 en el punto
en el punto
 es
es
 , si toda sucesión
, si toda sucesión
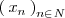 cuyos terminos son todos mayores que
cuyos terminos son todos mayores que
 y que tiende a
y que tiende a
 verifica
verifica
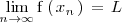
El límite por la derecha se denota por
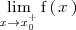 o bien
o bien
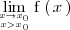
El que la anterior igualdad sea cierta significa que podemos hacer
 tan cercano a
tan cercano a
 como queramos eligiendo
como queramos eligiendo
 lo suficientemente proximo a
lo suficientemente proximo a
 por la derecha.
por la derecha.
Límite por la izquierda
Se dice que el límite por la izquierda de una función
 en el punto
en el punto
 es
es
 , si toda sucesión
, si toda sucesión
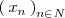 cuyos terminos son todos menores que
cuyos terminos son todos menores que
 y que tiende a
y que tiende a
 verifica
verifica
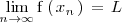
El límite por la izquierda se denota por
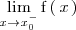 o bien
o bien
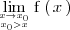
El que la anterior igualdad sea cierta significa que podemos hacer
 tan cercano a
tan cercano a
 como queramos eligiendo
como queramos eligiendo
 lo suficientemente proximo a
lo suficientemente proximo a
 por la izquierda.
por la izquierda.
Ejemplo
Consideremos la función
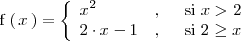
y calculemos ambos limites laterales cuando
 tiende a dos.
tiende a dos.
Como para valores de
 mayores que dos
mayores que dos
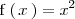
se tiene que
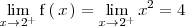
Para calcular el otro limite lateral, tenemos en cuenta que
cuando
 es menor que dos
es menor que dos
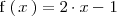
y, por lo tanto