Límite de una función
De Wikillerato
| Línea 200: | Línea 200: | ||
<br/> | <br/> | ||
| + | |||
| + | Aqui, la palabras '''''pequeño''''' ( '''''grande''''') la utilizamos de la siguiente manera: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | a | ||
| + | </math> | ||
| + | es mas pequeño ( grande ) que | ||
| + | <math> | ||
| + | b | ||
| + | </math> | ||
| + | si y solo si | ||
| + | | ||
| + | <math> | ||
| + | b > a \left( \, a > b \, \right) | ||
| + | </math>. | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 17:28 11 ago 2010
Tabla de contenidos |
Limite de f(x) cuando x tiende a un número real
El límite de la función
 , cuando
, cuando
 tiende a
tiende a
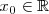 existe y es igual a
existe y es igual a
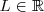 , si ambos límites laterales existen y son iguales a
, si ambos límites laterales existen y son iguales a
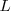 , es decir
, es decir
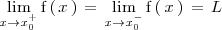
Lo expresamos de la siguiente manera:
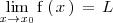
El que la anterior igualdad sea cierta significa que podemos hacer
 tan cercano a
tan cercano a
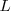 como queramos eligiendo
como queramos eligiendo
 lo suficientemente proximo a
lo suficientemente proximo a
 , por la derecha o por la izquierda.
, por la derecha o por la izquierda.
Limite de f(x) cuando x tiende a infinito
Se dice que el límite de la funcion
 , cuando
, cuando
 tiende a
tiende a
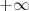 , es
, es
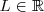 si cualquier sucesión
si cualquier sucesión
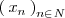 que tiende a
que tiende a
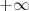 verifica que
verifica que
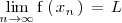 .
.
Lo expresamos como:
[Unparseable or potentially dangerous latex formula. Error 3 ]
El que la anterior igualdad sea cierta significa que podemos hacer
 tan cercano a
tan cercano a
 como queramos eligiendo
como queramos eligiendo
 lo suficientemente grande.
lo suficientemente grande.
Limite de f(x) cuando x tiende a menos infinito
Analogamente, se dice que el límite de la funcion
 , cuando
, cuando
 tiende a
tiende a
 , es
, es
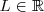 si cualquier sucesión
si cualquier sucesión
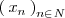 que tiende a
que tiende a
 verifica que
verifica que
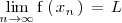 .
.
Lo expresamos como:
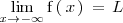
El que la anterior igualdad sea cierta significa que podemos hacer
 tan cercano a
tan cercano a
 como queramos eligiendo
como queramos eligiendo
 lo suficientemente pequeño.
lo suficientemente pequeño.
Aqui, la palabras pequeño ( grande) la utilizamos de la siguiente manera:
 es mas pequeño ( grande ) que
es mas pequeño ( grande ) que
 si y solo si
si y solo si
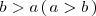 .
.



