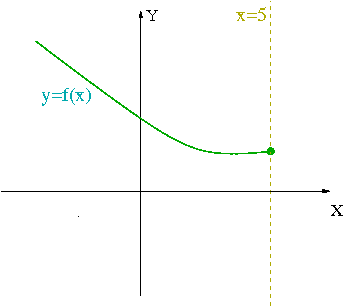Discontinuidades
De Wikillerato
(→Discontinuidad de primera especie) |
m (Revertidas las ediciones realizadas por 201.102.13.175 (Talk); a la última edición de Fjmolina) |
||
| (11 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | <br/> | ||
| + | |||
==Definición== | ==Definición== | ||
<br/> | <br/> | ||
| - | Una función es '''''discontinua''''' en | + | Una función es '''''discontinua''''' en <math> x \, = \, x_0 </math> si <math> \mathrm{f} </math> NO es continua en <math> x \, = \, x_0 </math>. |
| - | <math> | + | |
| - | x \, = \, x_0 | + | |
| - | </math> | + | |
| - | si | + | |
| - | <math> | + | |
| - | \mathrm{f} | + | |
| - | </math> | + | |
| - | | + | |
<br/> | <br/> | ||
| Línea 19: | Línea 13: | ||
<br/> | <br/> | ||
| - | + | Las discontinuidades se clasifican en: | |
| + | |||
| + | # 1. discontinuidades evitables, | ||
| + | |||
| + | # 2. discontinuidades de primera especie, y | ||
| + | |||
| + | # 3. discontinuidades de segunda especie. | ||
| + | |||
| + | Veamos, a continuación, cada uno de estos tipos de discontinuidad. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Discontinuidad evitable== | ||
<br/> | <br/> | ||
| Línea 27: | Línea 33: | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | tiene una '''''discontinuidad evitable''''' en | + | tiene una '''''discontinuidad evitable''''' en |
<math> | <math> | ||
x \, = \, x_0 | x \, = \, x_0 | ||
</math> | </math> | ||
| - | cuando existe el limite de la función | + | cuando |
| + | | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | NO es continua en | ||
| + | <math> | ||
| + | x \, = \, x_0 | ||
| + | </math> | ||
| + | | ||
| + | pero existe el limite de la función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | cuando | ||
| + | <math> | ||
| + | x | ||
| + | </math> | ||
| + | tiende a | ||
| + | <math> | ||
| + | x_0 | ||
| + | </math> | ||
| + | y este limite es finito. | ||
<br/> | <br/> | ||
| - | ==== | + | ===Nota sobre terminologia=== |
| + | |||
| + | <br/> | ||
| + | |||
| + | Cuando decimos que un limite existe queremos decir que el limite es un número | ||
| + | real, | ||
| + | <math> | ||
| + | \infty | ||
| + | </math> | ||
| + | o | ||
| + | <math> | ||
| + | -\infty | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Ejemplo== | ||
<br/> | <br/> | ||
| Línea 63: | Línea 107: | ||
<br/> | <br/> | ||
| - | no es continua en | + | no es continua en |
<math> | <math> | ||
x \, = \, 1 | x \, = \, 1 | ||
| Línea 92: | Línea 136: | ||
\lim_{x \to 1} \mathrm{f} \left( \, x \, \right) | \lim_{x \to 1} \mathrm{f} \left( \, x \, \right) | ||
</math> | </math> | ||
| - | existe, la discontinuidad que | + | existe y es finito, la discontinuidad que |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | tiene en | + | tiene en |
<math> | <math> | ||
x \, = \, 1 | x \, = \, 1 | ||
| Línea 104: | Línea 148: | ||
<br/> | <br/> | ||
| - | + | ==Discontinuidad de primera especie== | |
<br/> | <br/> | ||
| - | Una función presenta una '''''discontinuidad de primera especie | + | Una función |
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | presenta una '''''discontinuidad de primera especie''''' en | ||
<math> | <math> | ||
x \, = \, x_0 | x \, = \, x_0 | ||
</math> | </math> | ||
| - | si | + | si ambos limites laterales de |
<math> | <math> | ||
| - | f | + | \mathrm{f} |
</math> | </math> | ||
en | en | ||
| Línea 120: | Línea 168: | ||
x \, = \, x_0 | x \, = \, x_0 | ||
</math> | </math> | ||
| - | existen | + | existen y si se verifica alguna de las siguientes condiciones: |
| + | |||
| + | # 1. o bien, dichos limites laterales son finitos pero distintos: | ||
<br/> | <br/> | ||
| Línea 133: | Línea 183: | ||
<br/> | <br/> | ||
| - | ==== | + | # 2. o bien, alguno de los dos limites laterales no es finito. |
| + | |||
| + | <br/> | ||
| + | |||
| + | En el primer caso, cuando ambos limites laterales son distintos pero finitos, el | ||
| + | valor absoluto de la diferencia entre ambos limites | ||
| + | <center> | ||
| + | <math> | ||
| + | \left| \, | ||
| + | \lim_{x \to x_0^+} \mathrm{f} \left( \, x \, \right) \, - \, | ||
| + | \lim_{x \to x_0^-} \mathrm{f} \left( \, x \, \right) \, \right| | ||
| + | </math> | ||
| + | </center> | ||
| + | se conoce como el '''''salto de la discontinuidad'''''. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si la función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | tiene una discontinuidad de primera especie en | ||
| + | <math> | ||
| + | x = x_0 | ||
| + | </math> | ||
| + | pero dicha discontinuidad NO es de salto finito, entonces la gráfica de | ||
| + | <math> | ||
| + | \mathrm{f} | ||
| + | </math> | ||
| + | tiene una [[Asintotas#Asintotas verticales|asintota vertical]] de ecuación | ||
| + | <math> | ||
| + | x = x_0 | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo=== | ||
<br/> | <br/> | ||
| Línea 160: | Línea 246: | ||
<br/> | <br/> | ||
| - | no es continua en | + | no es continua en |
<math> | <math> | ||
x \, = \, 1 | x \, = \, 1 | ||
| Línea 186: | Línea 272: | ||
<br/> | <br/> | ||
| - | Como ambos limites laterales existen, la discontinuidad que | + | Como ambos limites laterales existen, pero son distintos, la discontinuidad que |
<math> | <math> | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | tiene en | + | tiene en |
<math> | <math> | ||
x \, = \, 1 | x \, = \, 1 | ||
| Línea 198: | Línea 284: | ||
<br/> | <br/> | ||
| - | + | El salto de la discontinuidad es | |
| + | <math> | ||
| + | 2 - 0 = 2 | ||
| + | </math> | ||
<br/> | <br/> | ||
| - | + | ===Ejemplo=== | |
| + | |||
| + | <br/> | ||
| + | |||
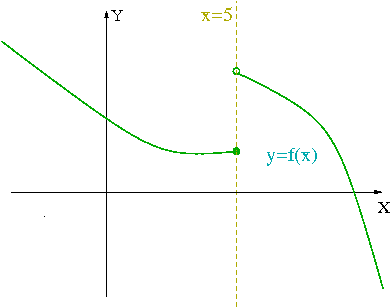
| + | Gráfica de una función con una discontinuidad de primera especie de salto finito en | ||
<math> | <math> | ||
| - | f | + | x = 5 |
| + | </math>: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | [[Imagen:primeraEspecie.png]] | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Discontinuidad de segunda especie== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Una función | ||
| + | <math> | ||
| + | \mathrm{f} | ||
</math> | </math> | ||
| - | + | presenta una '''''discontinuidad de segunda especie''''' en | |
<math> | <math> | ||
x \, = \, x_0 | x \, = \, x_0 | ||
</math> | </math> | ||
| - | si | + | si NO existe alguno de los limites laterales de |
<math> | <math> | ||
| - | f | + | \mathrm{f} |
</math> | </math> | ||
| - | + | en | |
| + | <math> | ||
| + | x_0 | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | ===Ejemplo=== | |
<br/> | <br/> | ||
| Línea 232: | Línea 345: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \mathrm{f} \left( \, x | + | \mathrm{f} \left( \, x \, \right) \, = \, \sqrt{x} |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
</math> | </math> | ||
</center> | </center> | ||
| Línea 245: | Línea 351: | ||
<br/> | <br/> | ||
| - | no es continua en | + | no es continua en |
<math> | <math> | ||
x \, = \, 0 | x \, = \, 0 | ||
| Línea 266: | Línea 372: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \lim_{x \to 0^-} \mathrm{f} \left( \, x | + | \not \exists \lim_{x \to 0^-} \mathrm{f} \left( \, x \, \right) |
</math> | </math> | ||
</center> | </center> | ||
| Línea 276: | Línea 382: | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | tiene en | + | tiene en |
<math> | <math> | ||
x \, = \, 0 | x \, = \, 0 | ||
| Línea 283: | Línea 389: | ||
<br/> | <br/> | ||
| + | |||
| + | No existe | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \lim_{x \to 0^-} \sqrt{x} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | porque | ||
| + | <math> | ||
| + | \sqrt{x} | ||
| + | </math> | ||
| + | no esta definida para valores negativos de | ||
| + | <math> | ||
| + | x | ||
| + | </math>. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ===Ejemplo=== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Gráfica de una función con una discontinuidad de segunda especie en | ||
| + | <math> | ||
| + | x = 5 | ||
| + | </math>: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | [[Imagen:segundaEspecie.png]] | ||
| + | </center> | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión actual
Tabla de contenidos |
Definición
Una función es discontinua ensi
NO es continua en
.
Tipos de discontinuidades
Las discontinuidades se clasifican en:
- 1. discontinuidades evitables,
- 2. discontinuidades de primera especie, y
- 3. discontinuidades de segunda especie.
Veamos, a continuación, cada uno de estos tipos de discontinuidad.
Discontinuidad evitable
Una función
 tiene una discontinuidad evitable en
tiene una discontinuidad evitable en
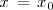 cuando
cuando
 NO es continua en
NO es continua en
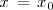 pero existe el limite de la función
pero existe el limite de la función
 cuando
cuando
 tiende a
tiende a
 y este limite es finito.
y este limite es finito.
Nota sobre terminologia
Cuando decimos que un limite existe queremos decir que el limite es un número
real,
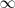 o
o
 .
.
Ejemplo
La función
 definida por:
definida por:
![\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{x^2 \, - \, 1}{x \, - \, 1} & , &
\quad \makebox{si}\quad x \neq 1
\\
3 & , & \quad \makebox{si} \quad x \, = \, 1
\end{array}
</pre>
<p>\right.
\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
\frac{x^2 \, - \, 1}{x \, - \, 1} & , &
\quad \makebox{si}\quad x \neq 1
\\
3 & , & \quad \makebox{si} \quad x \, = \, 1
\end{array}
</pre>
<p>\right.](/images/math/math-1bc6370d459059982d4cbf56b3625528.png)
no es continua en
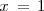 porque
porque
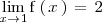 mientras que
mientras que
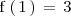 , es decir:
, es decir:
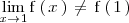
Como
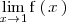 existe y es finito, la discontinuidad que
existe y es finito, la discontinuidad que
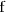 tiene en
tiene en
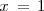 es evitable.
es evitable.
Discontinuidad de primera especie
Una función
 presenta una discontinuidad de primera especie en
presenta una discontinuidad de primera especie en
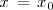 si ambos limites laterales de
si ambos limites laterales de
 en
en
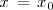 existen y si se verifica alguna de las siguientes condiciones:
existen y si se verifica alguna de las siguientes condiciones:
- 1. o bien, dichos limites laterales son finitos pero distintos:
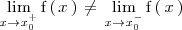
- 2. o bien, alguno de los dos limites laterales no es finito.
En el primer caso, cuando ambos limites laterales son distintos pero finitos, el valor absoluto de la diferencia entre ambos limites
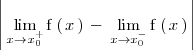
se conoce como el salto de la discontinuidad.
Si la función
 tiene una discontinuidad de primera especie en
tiene una discontinuidad de primera especie en
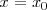 pero dicha discontinuidad NO es de salto finito, entonces la gráfica de
pero dicha discontinuidad NO es de salto finito, entonces la gráfica de
 tiene una asintota vertical de ecuación
tiene una asintota vertical de ecuación
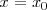 .
.
Ejemplo
La función
 definida por:
definida por:
![\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x^2 \, + \, 1 & , & \quad \makebox{si} \quad 1 \ge x
\\
x \, - \, 1 & , & \quad \makebox{si} \quad x \, > \, 1
\end{array}
</pre>
<p>\right.
\mathrm{f} \left( \, x \, \right) \, = \,
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x^2 \, + \, 1 & , & \quad \makebox{si} \quad 1 \ge x
\\
x \, - \, 1 & , & \quad \makebox{si} \quad x \, > \, 1
\end{array}
</pre>
<p>\right.](/images/math/math-b4e00ff82dd6d614ad2d9cc1fc106612.png)
no es continua en
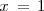 porque
porque
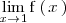 no existe, al ser ambos limites laterales distintos:
no existe, al ser ambos limites laterales distintos:
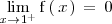
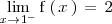
Como ambos limites laterales existen, pero son distintos, la discontinuidad que
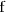 tiene en
tiene en
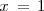 es de primera especie.
es de primera especie.
El salto de la discontinuidad es
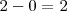
Ejemplo
Gráfica de una función con una discontinuidad de primera especie de salto finito en
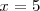 :
:
Discontinuidad de segunda especie
Una función
 presenta una discontinuidad de segunda especie en
presenta una discontinuidad de segunda especie en
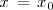 si NO existe alguno de los limites laterales de
si NO existe alguno de los limites laterales de
 en
en
 .
.
Ejemplo
La función
 definida por:
definida por:
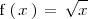
no es continua en
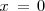 porque
porque
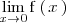 no existe, al no existir el limite por la izquierda de
no existe, al no existir el limite por la izquierda de
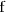 cuando
cuando
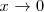 :
:
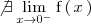
Como este limite por la izquierda no existe,
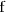 tiene en
tiene en
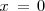 una discontinuidad de segunda especie.
una discontinuidad de segunda especie.
No existe
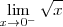
porque
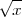 no esta definida para valores negativos de
no esta definida para valores negativos de
 .
.
Ejemplo
Gráfica de una función con una discontinuidad de segunda especie en
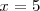 :
: