¿Qué es una matriz?
De Wikillerato
| Línea 1: | Línea 1: | ||
| + | |||
| + | |||
__TOC__ | __TOC__ | ||
| Línea 46: | Línea 48: | ||
se puede denotar tambien como | se puede denotar tambien como | ||
<math> | <math> | ||
| - | \quad A = \left( a_{ij} \right) \quad | + | \quad \mathbf{A} = \left( a_{ij} \right) \quad |
</math> | </math> | ||
donde | donde | ||
| Línea 76: | Línea 78: | ||
<br/> | <br/> | ||
| - | + | ==Tipos de matrices== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | ==Matrices cuadradas== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Las matrices cuadradas son aquellas que tienen el mismo número de filas que de | |
| - | + | columnas. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | En las matrices cuadradas tenemos: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | |||
| - | |||
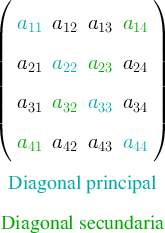
* la diagonal principal formada por los elementos de la forma | * la diagonal principal formada por los elementos de la forma | ||
| Línea 120: | Línea 101: | ||
| | ||
| - | *la diagonal secundaria formada por los elementos de la forma | + | * la diagonal secundaria formada por los elementos de la forma |
<math> | <math> | ||
a_{ij} | a_{ij} | ||
| Línea 137: | Línea 118: | ||
<br/> | <br/> | ||
| - | Una '''''matriz rectangular''''' es aquella que tiene distinto número de filas que de columnas | + | <br/> |
| - | + | ||
| - | + | ===Matriz rectangular=== | |
| - | + | ||
| - | + | <br/> | |
| - | + | ||
| - | </ | + | Una '''''matriz rectangular''''' es aquella que tiene distinto número de filas |
| - | + | que de columnas. Si una matriz NO es cuadrada tiene que ser rectangular. | |
| + | |||
| + | <br/> | ||
====Ejemplo de matriz rectangular==== | ====Ejemplo de matriz rectangular==== | ||
| Línea 164: | Línea 147: | ||
<br/> | <br/> | ||
| - | ''''' | + | ===Matriz fila=== |
| + | |||
| + | <br/> | ||
| + | |||
| + | Una '''''matriz fila''''' es una matriz con una sola fila. Su dimensi\'on es | ||
<math> | <math> | ||
1 \times n | 1 \times n | ||
</math> | </math> | ||
. | . | ||
| - | ====Ejemplo | + | |
| + | <br/> | ||
| + | |||
| + | ====Ejemplo==== | ||
<br/> | <br/> | ||
| Línea 185: | Línea 175: | ||
<br/> | <br/> | ||
| - | ''''' | + | ===Matriz columna=== |
| + | |||
| + | <br/> | ||
| + | |||
| + | Una '''''matriz columna''''' es una matriz rectangular con una sola columna. Su | ||
| + | dimension es | ||
<math> | <math> | ||
m \times 1 | m \times 1 | ||
| Línea 191: | Línea 186: | ||
. | . | ||
| - | ====Ejemplo | + | <br/> |
| + | |||
| + | ====Ejemplo==== | ||
<br/> | <br/> | ||
| Línea 209: | Línea 206: | ||
<br/> | <br/> | ||
| - | == | + | ==Ejemplo== |
<br/> | <br/> | ||
| - | Una '''''matriz nula''''' es una matriz | + | Una '''''matriz nula''''' es una matriz cuyos elementos sont todos nulos. Se denota |
por | por | ||
<math> | <math> | ||
| - | \mathbf{0} | + | \mathbf{0}_{m \times n} |
</math> | </math> | ||
. | . | ||
| - | ====Ejemplo | + | |
| + | <br/> | ||
| + | |||
| + | Donde | ||
| + | <math> | ||
| + | m \times n | ||
| + | </math> | ||
| + | es la dimensión de la matriz. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ====Ejemplo==== | ||
<br/> | <br/> | ||
| Línea 237: | Línea 245: | ||
<br/> | <br/> | ||
| - | ''''' | + | ===Matriz triangular superior=== |
| + | |||
| + | <br/> | ||
| + | |||
| + | Una '''''matriz triangular superior''''' es una matriz cuadrada en la que todos los terminos | ||
situados por debajo de la diagonal principal son ceros. | situados por debajo de la diagonal principal son ceros. | ||
| - | ====Ejemplo | + | <br/> |
| + | |||
| + | ====Ejemplo==== | ||
<br/> | <br/> | ||
| Línea 260: | Línea 274: | ||
<br/> | <br/> | ||
| - | ''''' | + | ==Matriz triangular inferior== |
| + | |||
| + | <br/> | ||
| + | |||
| + | Una '''''matriz triangular inferior''''' es una matriz cuadrada en la que todos los terminos | ||
situados por encima de la diagonal principal son ceros. | situados por encima de la diagonal principal son ceros. | ||
| - | ====Ejemplo | + | <br/> |
| + | |||
| + | ====Ejemplo ==== | ||
<br/> | <br/> | ||
| Línea 280: | Línea 300: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
<br/> | <br/> | ||
| - | ''''' | + | ===Matriz diagonal=== |
| - | + | ||
| + | <br/> | ||
| + | |||
| + | Una '''''matriz diagonal''''' es una matriz cuadrada en la que todos los terminos | ||
| + | NO situados en la diagonal principal son ceros. | ||
| + | |||
| + | <br/> | ||
| - | ====Ejemplo | + | ====Ejemplo==== |
<br/> | <br/> | ||
| Línea 306: | Línea 333: | ||
<br/> | <br/> | ||
| - | ''''' | + | ===Matriz escalar=== |
| + | |||
| + | <br/> | ||
| + | |||
| + | Una '''''matriz escalar''''' es una matriz diagonal en la que todos los terminos | ||
de la diagonal principal son iguales. | de la diagonal principal son iguales. | ||
| - | ====Ejemplo | + | <br/> |
| + | |||
| + | ====Ejemplo==== | ||
<br/> | <br/> | ||
| Línea 329: | Línea 362: | ||
<br/> | <br/> | ||
| - | ''''' | + | ==Matriz unidad o identidad== |
| + | |||
| + | <br/> | ||
| + | |||
| + | Una '''''matriz unidad o identidad''''' es una matriz escalar cuyos elementos en la diagonal principal son | ||
todos 1. | todos 1. | ||
| - | ====Ejemplo | + | <br/> |
| + | |||
| + | ====Ejemplo==== | ||
<br/> | <br/> | ||
Revisión de 08:07 3 oct 2010
Tabla de contenidos |
Definición de matriz
Una matriz es un cuadrado o tabla de numeros ordenados. Se llama matriz de dimension
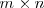 a un conjunto de números reales dispuestos en
a un conjunto de números reales dispuestos en
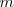 filas y
filas y
 columnas de la siguiente forma
columnas de la siguiente forma
![\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11 }& a_{12} & \ldots & a_{1n}
\\
a_{21 }& a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1 }& a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)](/images/math/math-2b93b39c0505fe91a8bdffdcb317c676.png)
La matriz
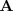 se puede denotar tambien como
se puede denotar tambien como
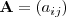 donde
donde
![\left\{
</p>
<pre> \begin{array}[c]{l}
i = 1, \, 2, \, \ldots, \, m
\\
j = 1, \, 2, \, \ldots, \, n
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{l}
i = 1, \, 2, \, \ldots, \, m
\\
j = 1, \, 2, \, \ldots, \, n
\end{array}
</pre>
<p>\right.](/images/math/math-22d889e2bbcf6ec56d6db3849ebbe730.png)
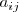 designa un elemento generico de la matriz
designa un elemento generico de la matriz
 , el elemento que se encuentra en la i-esima fila y j-esima columna.
, el elemento que se encuentra en la i-esima fila y j-esima columna.
Tipos de matrices
Matrices cuadradas
Las matrices cuadradas son aquellas que tienen el mismo número de filas que de columnas.
En las matrices cuadradas tenemos:
- la diagonal principal formada por los elementos de la forma
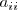
- la diagonal secundaria formada por los elementos de la forma
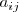 tales que
tales que
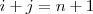
Matriz rectangular
Una matriz rectangular es aquella que tiene distinto número de filas que de columnas. Si una matriz NO es cuadrada tiene que ser rectangular.
Ejemplo de matriz rectangular
![</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & -1 & ~~0
\\
2 & ~~3 & -1
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & -1 & ~~0
\\
2 & ~~3 & -1
\end{array}
\right)
</pre>
<p>](/images/math/math-77539f199b63acde3f386891e6643924.png)
Matriz fila
Una matriz fila es una matriz con una sola fila. Su dimensi\'on es
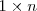 .
.
Ejemplo
![</p>
<pre> \left(
\begin{array}[c]{ccc}
-1 & 3 & 5
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
-1 & 3 & 5
\end{array}
\right)
</pre>
<p>](/images/math/math-ddcaa947e9641f093ec0f8d2c0d583d9.png)
Matriz columna
Una matriz columna es una matriz rectangular con una sola columna. Su
dimension es
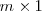 .
.
Ejemplo
![</p>
<pre> \left(
\begin{array}[c]{c}
-1
\\
~~3
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{c}
-1
\\
~~3
\end{array}
\right)
</pre>
<p>](/images/math/math-6e25da3e668f5afabb9e8999290f43de.png)
Ejemplo
Una matriz nula es una matriz cuyos elementos sont todos nulos. Se denota
por
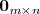 .
.
Donde
 es la dimensión de la matriz.
es la dimensión de la matriz.
Ejemplo
![</p>
<pre> \left(
\begin{array}[c]{ccc}
0 & 0 & 0
\\
0 & 0 & 0
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
0 & 0 & 0
\\
0 & 0 & 0
\end{array}
\right)
</pre>
<p>](/images/math/math-5843638a226353656790577733c70017.png)
Matriz triangular superior
Una matriz triangular superior es una matriz cuadrada en la que todos los terminos situados por debajo de la diagonal principal son ceros.
Ejemplo
![</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & -1 & ~~0
\\
0 & ~~3 & -1
\\
0 & ~~0 & ~~2
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & -1 & ~~0
\\
0 & ~~3 & -1
\\
0 & ~~0 & ~~2
\end{array}
\right)
</pre>
<p>](/images/math/math-bc3f0df47bfb80a397ae4b8f23b8c0aa.png)
Matriz triangular inferior
Una matriz triangular inferior es una matriz cuadrada en la que todos los terminos situados por encima de la diagonal principal son ceros.
Ejemplo
![</p>
<pre> \left(
\begin{array}[c]{ccc}
2 & ~~0 & 0
\\
3 & -1 & 0
\\
1 & -1 & 3
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
2 & ~~0 & 0
\\
3 & -1 & 0
\\
1 & -1 & 3
\end{array}
\right)
</pre>
<p>](/images/math/math-82e48a12244d0a664439764d8460b342.png)
Matriz diagonal
Una matriz diagonal es una matriz cuadrada en la que todos los terminos NO situados en la diagonal principal son ceros.
Ejemplo
![</p>
<pre> \left(
\begin{array}[c]{ccc}
~~2 & ~~0 & ~~0
\\
~~0 & -1 & ~~0
\\
~~0 & ~~0 & ~~3
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
~~2 & ~~0 & ~~0
\\
~~0 & -1 & ~~0
\\
~~0 & ~~0 & ~~3
\end{array}
\right)
</pre>
<p>](/images/math/math-7243130e96bfab5fa81a6d6c3f538afa.png)
Matriz escalar
Una matriz escalar es una matriz diagonal en la que todos los terminos de la diagonal principal son iguales.
Ejemplo
![</p>
<pre> \left(
\begin{array}[c]{ccc}
2 & {0} & {0}
\\
{0} & 2 & {0}
\\
{0} & {0} & 2
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
2 & {0} & {0}
\\
{0} & 2 & {0}
\\
{0} & {0} & 2
\end{array}
\right)
</pre>
<p>](/images/math/math-0c8108a994f140b623c5323aab03f2e4.png)
Matriz unidad o identidad
Una matriz unidad o identidad es una matriz escalar cuyos elementos en la diagonal principal son todos 1.
Ejemplo
![</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & {0} & {0}
\\
{0} & 1 & {0}
\\
{0} & {0} & 1
\end{array}
\right)
</pre>
<p>
</p>
<pre> \left(
\begin{array}[c]{ccc}
1 & {0} & {0}
\\
{0} & 1 & {0}
\\
{0} & {0} & 1
\end{array}
\right)
</pre>
<p>](/images/math/math-992b5c285926278d809ff3bdadf8a15d.png)