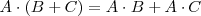Operaciones elementales con matrices
De Wikillerato
| Línea 1: | Línea 1: | ||
| - | + | ==Suma de matrices== | |
| - | + | ||
| + | <br/> | ||
Para dos matrices | Para dos matrices | ||
| Línea 38: | Línea 39: | ||
<br/> | <br/> | ||
| - | Ejemplo: | + | ====Ejemplo:==== |
<br/> | <br/> | ||
| Línea 76: | Línea 77: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Producto de un numero por una matriz== | ||
<br/> | <br/> | ||
| Línea 114: | Línea 119: | ||
se obtiene multiplicando el numero real por cada uno de los elementos de la | se obtiene multiplicando el numero real por cada uno de los elementos de la | ||
matriz. | matriz. | ||
| - | Ejemplo: | + | |
| + | <br/> | ||
| + | |||
| + | ====Ejemplo:==== | ||
<br/> | <br/> | ||
| Línea 142: | Línea 150: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Producto de matrices== | ||
<br/> | <br/> | ||
| Línea 195: | Línea 207: | ||
se obtiene multiplicando la fila i-ésima de la primera matriz por la columna | se obtiene multiplicando la fila i-ésima de la primera matriz por la columna | ||
k-ésima de la segunda matriz. | k-ésima de la segunda matriz. | ||
| - | Ejemplo: | + | |
| + | <br/> | ||
| + | |||
| + | ====Ejemplo:==== | ||
<br/> | <br/> | ||
| Línea 231: | Línea 246: | ||
<br/> | <br/> | ||
| - | + | ===Propiedades del producto de matrices=== | |
| + | |||
| + | <br/> | ||
| + | |||
| + | 1. El producto de matrices cuadradas es asociativo: | ||
<br/> | <br/> | ||
| Línea 251: | Línea 270: | ||
<br/> | <br/> | ||
| - | + | 2. El producto de matrices cuadradas de orden | |
<math> | <math> | ||
n | n | ||
| Línea 275: | Línea 294: | ||
<br/> | <br/> | ||
| - | + | 3. El producto de matrices cuadradas es distributivo respecto de la suma de matrices: | |
<br/> | <br/> | ||
Revisión de 12:42 29 nov 2006
Tabla de contenidos |
Suma de matrices
Para dos matrices
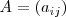 y
y
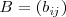 de la misma dimension
de la misma dimension
 , la suma de
, la suma de
 y
y
 es la matriz de la misma dimension
es la matriz de la misma dimension
 , dada por
, dada por
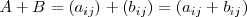
Ejemplo:
![A + B =
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 }& a_{12} & a_{13}
\\
a_{21 }& a_{22} & a_{23}
\\
a_{31 }& a_{32} & a_{33}
\end{array}
</pre>
<p>\right)
+
\left(
</p>
<pre> \begin{array}[c]{ccc}
b_{11 }& b_{12} & b_{13}
\\
b_{21 }& b_{22} & b_{23}
\\
b_{31 }& b_{32} & b_{33}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 } + b_{11 } & a_{12} + b_{12} & a_{13} + b_{13}
\\
a_{21 } + b_{21 } & a_{22} + b_{22} & a_{23} + b_{23}
\\
a_{31 } + b_{31 } & a_{32} + b_{32} & a_{33} + b_{33}
\end{array}
</pre>
<p>\right)
A + B =
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 }& a_{12} & a_{13}
\\
a_{21 }& a_{22} & a_{23}
\\
a_{31 }& a_{32} & a_{33}
\end{array}
</pre>
<p>\right)
+
\left(
</p>
<pre> \begin{array}[c]{ccc}
b_{11 }& b_{12} & b_{13}
\\
b_{21 }& b_{22} & b_{23}
\\
b_{31 }& b_{32} & b_{33}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_{11 } + b_{11 } & a_{12} + b_{12} & a_{13} + b_{13}
\\
a_{21 } + b_{21 } & a_{22} + b_{22} & a_{23} + b_{23}
\\
a_{31 } + b_{31 } & a_{32} + b_{32} & a_{33} + b_{33}
\end{array}
</pre>
<p>\right)](/images/math/math-83b07e70030828d73f75b5a4cd132a90.png)
Producto de un numero por una matriz
Para un número real
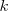 y una matriz
y una matriz
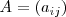 de dimension
de dimension
 , el producto de un número real por una matriz es la matriz de la misma dimension
, el producto de un número real por una matriz es la matriz de la misma dimension
 dada por
dada por
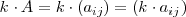
Es decir, el producto
 se obtiene multiplicando el numero real por cada uno de los elementos de la
matriz.
se obtiene multiplicando el numero real por cada uno de los elementos de la
matriz.
Ejemplo:
![k \cdot A = k \cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
a_{11 }& a_{12}
\\
a_{21 }& a_{22}
\\
a_{31 }& a_{32}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
k \cdot a_{11 }& k \cdot a_{12}
\\
k \cdot a_{21 }& k \cdot a_{22}
\\
k \cdot a_{31 }& k \cdot a_{32}
\end{array}
</pre>
<p>\right)
k \cdot A = k \cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
a_{11 }& a_{12}
\\
a_{21 }& a_{22}
\\
a_{31 }& a_{32}
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
k \cdot a_{11 }& k \cdot a_{12}
\\
k \cdot a_{21 }& k \cdot a_{22}
\\
k \cdot a_{31 }& k \cdot a_{32}
\end{array}
</pre>
<p>\right)](/images/math/math-ac0775a178d76f16f0d842a39ec92976.png)
Producto de matrices
El producto de dos matrices
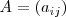 de dimension
de dimension
 y
y
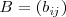 de dimension
de dimension
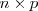 , es la matriz
, es la matriz
 dada por:
dada por:
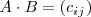
con
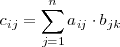
Es decir, cada elemento
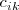 se obtiene multiplicando la fila i-ésima de la primera matriz por la columna
k-ésima de la segunda matriz.
se obtiene multiplicando la fila i-ésima de la primera matriz por la columna
k-ésima de la segunda matriz.
Ejemplo:
![\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
4 & 5 & 6
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
~~7 & ~~8
\\
~~9 & ~~0
\\
-1 & -2
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 \cdot 7 + 2 \cdot 9 + 3 \cdot \left( -1 \right) & 1 \cdot 8 + 2 \cdot 0 + 3 \cdot \left( -2 \right)
\\
4 \cdot 7 + 5 \cdot 9 + 6 \cdot \left( -1 \right) & 4 \cdot 8 + 5 \cdot 0 + 6 \cdot \left( -2 \right)
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
4 & 5 & 6
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{cc}
~~7 & ~~8
\\
~~9 & ~~0
\\
-1 & -2
\end{array}
</pre>
<p>\right)
=
\left(
</p>
<pre> \begin{array}[c]{cc}
1 \cdot 7 + 2 \cdot 9 + 3 \cdot \left( -1 \right) & 1 \cdot 8 + 2 \cdot 0 + 3 \cdot \left( -2 \right)
\\
4 \cdot 7 + 5 \cdot 9 + 6 \cdot \left( -1 \right) & 4 \cdot 8 + 5 \cdot 0 + 6 \cdot \left( -2 \right)
\end{array}
</pre>
<p>\right)](/images/math/math-2ff8eff26cdd9448d6141d459441e2d9.png)
Propiedades del producto de matrices
1. El producto de matrices cuadradas es asociativo:
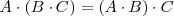
2. El producto de matrices cuadradas de orden
 posee como elemento neutro la matriz unidad o identidad
posee como elemento neutro la matriz unidad o identidad
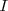 de orden
de orden
 ya que:
ya que:
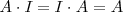
3. El producto de matrices cuadradas es distributivo respecto de la suma de matrices: