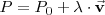Definición de una recta
De Wikillerato
(Diferencias entre revisiones)
| Línea 35: | Línea 35: | ||
del espacio que verifican la relacion vectorial | del espacio que verifican la relacion vectorial | ||
<math> | <math> | ||
| - | \stackrel | + | \stackrel{\longrightarrow}{P_oP} = \lambda \vec {\mathbf{v}} |
</math> | </math> | ||
con | con | ||
| Línea 41: | Línea 41: | ||
\lambda \in R | \lambda \in R | ||
</math> | </math> | ||
| - | + | ||
| + | <br/> | ||
| + | |||
[[Imagen:recta.gif]] | [[Imagen:recta.gif]] | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Teniendo en cuenta la suma de vectores se verifica que: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \stackrel{\longrightarrow}{OP} \, = \, \stackrel{\longrightarrow}{OP_0} + | ||
| + | \stackrel{\longrightarrow}{P_0P} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si identificamos el punto | ||
| + | <math> | ||
| + | P | ||
| + | </math> | ||
| + | con el vector que va desde el origen de coordenadas hasta el punto | ||
| + | <math> | ||
| + | P, | ||
| + | </math> | ||
| + | | ||
| + | <math> | ||
| + | \stackrel{\longrightarrow}{OP}, | ||
| + | </math> | ||
| + | se tiene que | ||
| + | <math> | ||
| + | P = P_0 + \lambda \cdot \vec{\mathbf{v}} | ||
| + | </math> | ||
Revisión de 19:26 30 nov 2006
Al igual que ocurre en el plano, una recta en el espacio queda determinada conociendo un
punto
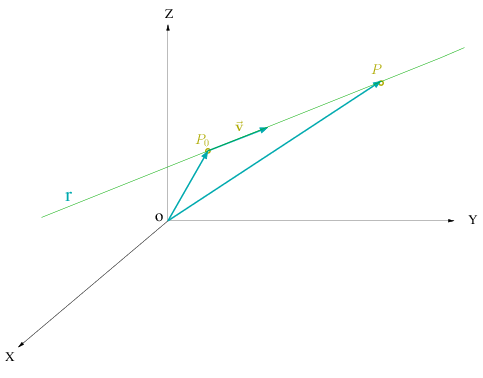
 y un vector no nulo
y un vector no nulo
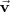 que se llama vector director o direccional de la recta.
que se llama vector director o direccional de la recta.
Estudiamos a continuacion las diferentes formas que puede adoptar la ecuacion de una recta.
Ecuacion en forma vectorial
La recta que pasa por el punto
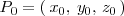 y tiene por vector director
y tiene por vector director
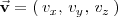 es el conjunto de puntos
es el conjunto de puntos
 del espacio que verifican la relacion vectorial
del espacio que verifican la relacion vectorial
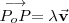 con
con
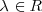
Teniendo en cuenta la suma de vectores se verifica que:
[Unparseable or potentially dangerous latex formula. Error 3 ]
Si identificamos el punto
 con el vector que va desde el origen de coordenadas hasta el punto
con el vector que va desde el origen de coordenadas hasta el punto
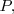 [Unparseable or potentially dangerous latex formula. Error 3 ]
se tiene que
[Unparseable or potentially dangerous latex formula. Error 3 ]
se tiene que