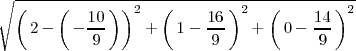Problemas de distancias
De Wikillerato
| Línea 253: | Línea 253: | ||
</math> | </math> | ||
es | es | ||
| + | |||
| + | <br/> | ||
| + | |||
<center> | <center> | ||
<math> | <math> | ||
| Línea 265: | Línea 268: | ||
\right| | \right| | ||
= \left( \, x - 2, \, y - 1, \, z - 0 \, \right) \cdot \left( \, 3, \, 6, \, 3 | = \left( \, x - 2, \, y - 1, \, z - 0 \, \right) \cdot \left( \, 3, \, 6, \, 3 | ||
| - | \, \right) = 3 \cdot | + | \, \right) = |
| + | </math> | ||
| + | </center> | ||
| + | <center> | ||
| + | <math> | ||
| + | = 3 \cdot \left( \, x - 2 \, \right) + 6 \cdot \left( \, y - 1 \, | ||
\right) + 3 \cdot \left( \, z - 0 \, \right) = 3x + 6y + 3z -12 = 0 | \right) + 3 \cdot \left( \, z - 0 \, \right) = 3x + 6y + 3z -12 = 0 | ||
\right| | \right| | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
donde la primera fila del determinante es el vector | donde la primera fila del determinante es el vector | ||
<math> | <math> | ||
| Línea 282: | Línea 293: | ||
</math> | </math> | ||
es, pues, la solución del sistema de ecuaciones | es, pues, la solución del sistema de ecuaciones | ||
| + | |||
| + | <br/> | ||
| + | |||
<center> | <center> | ||
<math> | <math> | ||
| + | \left\{ | ||
\begin{array}{l} | \begin{array}{l} | ||
0 = 3x + 6y + 3z -12 | 0 = 3x + 6y + 3z -12 | ||
| Línea 291: | Línea 306: | ||
0 = 2x - y + 4 | 0 = 2x - y + 4 | ||
\end{array} | \end{array} | ||
| + | \right. | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
Restando a la tercera ecuación la primera y la segunda se tiene que | Restando a la tercera ecuación la primera y la segunda se tiene que | ||
| + | |||
| + | <br/> | ||
| + | |||
<center> | <center> | ||
<math> | <math> | ||
| Línea 299: | Línea 321: | ||
</math> | </math> | ||
</center> | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
con lo cual | con lo cual | ||
<math> | <math> | ||
| Línea 318: | Línea 343: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | x = | + | x = \frac{y}{2} - 2 = \frac{8}{9} - 2 = -\frac{10}{9} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 349: | Línea 374: | ||
<math> | <math> | ||
z = \frac{1}{3} \cdot \left( \, 2y - x \, \right) = \frac{1}{3} \cdot \left( \, | z = \frac{1}{3} \cdot \left( \, 2y - x \, \right) = \frac{1}{3} \cdot \left( \, | ||
| - | 2 \cdot \frac{16}{9} | + | 2 \cdot \frac{16}{9} + \frac{10}{9} \, \right) = \frac{42}{27} = \frac{14}{9} |
</math> | </math> | ||
</center> | </center> | ||
| Línea 372: | Línea 397: | ||
<center> | <center> | ||
<math> | <math> | ||
| - | \sqrt{\left( \, 2 - \frac{10}{9} \, \right)^2 + \left( \, 1 - \frac{16}{9} \, \right)^2 + \left( \, 0 - | + | \sqrt{\left( \, 2 - \left( \, -\frac{10}{9} \, \right) \right)^2 + \left( \, 1 - \frac{16}{9} \, \right)^2 + \left( \, 0 - |
| - | \frac{ | + | \frac{14}{9} \, \right)^2} |
</math> | </math> | ||
</center> | </center> | ||
| - | |||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 12:43 30 oct 2010
Distancia entre dos puntos
La distancia entre dos puntos
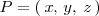 y
y
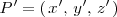 es
es
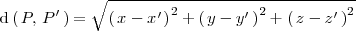
Distancia entre un punto y una recta
La distancia de un punto
 a una recta
a una recta
 es la distancia entre
es la distancia entre
 y su proyeccion
y su proyeccion
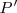 en la recta
en la recta
 .
.
Ejemplo
Calculemos la distancia del punto
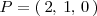 a la recta
a la recta
 de ecuaciones
de ecuaciones
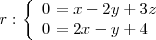
Sea
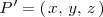 la proyección del punto
la proyección del punto
 en la recta
en la recta
 .
Queremos calcular la distancia de
.
Queremos calcular la distancia de
 a
a
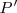 y para ello necesitamos conocer
y para ello necesitamos conocer
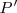 .
.
Para hallar
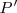 vamos a resolver un sistema de tres ecuaciones, dos de ellas son las de la recta
vamos a resolver un sistema de tres ecuaciones, dos de ellas son las de la recta
 y la otra ecuación procede de igualar a cero el producto escalar del vector
y la otra ecuación procede de igualar a cero el producto escalar del vector
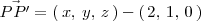
por un vector director de la recta
 .
El producto escalar de ambos vectores es cero porque son perpendiculares (la recta que pasa por
.
El producto escalar de ambos vectores es cero porque son perpendiculares (la recta que pasa por
 y
y
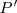 es perpendicular a la recta
es perpendicular a la recta
 ).
).
Podemos obtener un vector director
 de la recta
de la recta
 multiplicando vectorialmente un vector perpendicular al plano
multiplicando vectorialmente un vector perpendicular al plano
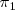 por un vector perpendicular al plano
por un vector perpendicular al plano
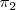 .
.
Un vector
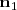 perpendicular al plano
perpendicular al plano
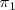 lo podemos obtener de los coeficientes de x, y, z en la ecuación de
lo podemos obtener de los coeficientes de x, y, z en la ecuación de
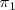 :
:
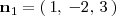
De la misma forma obtenemos un vector
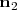 perpendicular al plano
perpendicular al plano
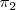 :
:
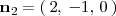
El producto vectorial de ambos vectores,
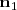 y
y
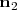 es
es

donde
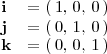
El producto escalar de
 por
por
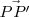 es
es
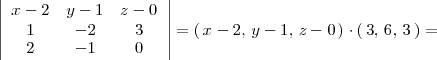
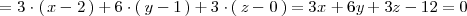
donde la primera fila del determinante es el vector
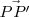 .
.
El punto
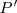 es, pues, la solución del sistema de ecuaciones
es, pues, la solución del sistema de ecuaciones
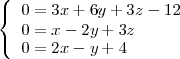
Restando a la tercera ecuación la primera y la segunda se tiene que
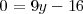
con lo cual
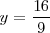 .
Sustituyendo
.
Sustituyendo
 por
por
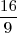 en la tercera ecuación del sistema y despejando
en la tercera ecuación del sistema y despejando
 se llega a que
se llega a que
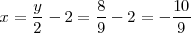
Finalmente, sustituyendo
 por
por
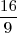 y
y
 por
[Unparseable or potentially dangerous latex formula. Error 3 ]
en la segunda ecuación del sistema y despejando
por
[Unparseable or potentially dangerous latex formula. Error 3 ]
en la segunda ecuación del sistema y despejando
 se llega a que
se llega a que
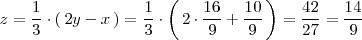
La distancia de
 a
a
 coincide con la distancia de
coincide con la distancia de
 a
a
 y esta es:
y esta es: