Resolución de triángulos
De Wikillerato
| Línea 4: | Línea 4: | ||
<br/> | <br/> | ||
| - | Los angulos de un | + | Los angulos de un triángulo suman |
<math> | <math> | ||
\pi | \pi | ||
| Línea 16: | Línea 16: | ||
\beta | \beta | ||
</math> | </math> | ||
| - | de un | + | de un triángulo podemos hallar el tercero, |
<math> | <math> | ||
\gamma | \gamma | ||
| Línea 171: | Línea 171: | ||
</center> | </center> | ||
Una vez realizado este calculo se procede como se ha descrito antes en el caso | Una vez realizado este calculo se procede como se ha descrito antes en el caso | ||
| - | de que se tengan [[Resolución de | + | de que se tengan [[Resolución de triángulos#Conocemos un lado y dos angulos|dos angulos y un lado]]. |
<br/> | <br/> | ||
| Línea 179: | Línea 179: | ||
<br/> | <br/> | ||
| - | En este caso hay que determinar todos y cada uno de los ángulos del | + | En este caso hay que determinar todos y cada uno de los ángulos del triángulo. |
Para ello se utiliza el teorema del coseno. Por ejemplo, de | Para ello se utiliza el teorema del coseno. Por ejemplo, de | ||
<center> | <center> | ||
| Línea 193: | Línea 193: | ||
</center> | </center> | ||
Analogamente, se tiene que: | Analogamente, se tiene que: | ||
| + | |||
| + | <br/> | ||
| + | |||
<center> | <center> | ||
<math> | <math> | ||
\begin{array}{l} | \begin{array}{l} | ||
\beta = \mathrm{arc} \cos \frac{a^2 + c^2 - b^2}{2ac} | \beta = \mathrm{arc} \cos \frac{a^2 + c^2 - b^2}{2ac} | ||
| + | \\ | ||
\\ | \\ | ||
\gamma = \mathrm{arc} \cos \frac{a^2 + b^2 - c^2}{2ab} | \gamma = \mathrm{arc} \cos \frac{a^2 + b^2 - c^2}{2ab} | ||
Revisión de 00:10 6 nov 2010
Tabla de contenidos |
Conocemos un lado y dos angulos
Los angulos de un triángulo suman
 radianes, por lo tanto, si conocemos dos angulos
radianes, por lo tanto, si conocemos dos angulos
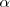 y
y
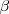 de un triángulo podemos hallar el tercero,
de un triángulo podemos hallar el tercero,
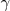 utilizando la igualdad:
utilizando la igualdad:
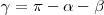
Supongamos que, ademas, conocemos la longitud del lado
 y que queremos conocer la longitud de los otros dos lados
y que queremos conocer la longitud de los otros dos lados
 y
y
 ,
,
Para hallar
 podemos utilizar el teorema del seno:
podemos utilizar el teorema del seno:
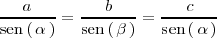
Del que se deduce que
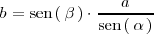
Analogamente, se deduce que
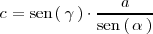
Conocemos dos lados y el angulo que forman
Supongamos que conocemos
 ,
,
 y
y
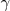 .
.
En este caso se utiliza el teorema del coseno
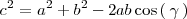
para calcular
 :
:
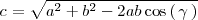
Una vez hallado c, calculamos
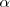 y
y
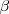 mediante el teorema del seno:
mediante el teorema del seno:
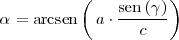
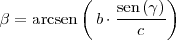
Conocemos dos lados y otro angulo que no es el angulo que forman
Supongamos que se conocen los lados
 y
y
 y el ángulo
y el ángulo
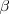 .
.
Podemos utilizar el teorema del seno para hallar
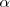 :
:
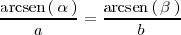
con lo cual
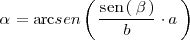
Una vez realizado este calculo se procede como se ha descrito antes en el caso de que se tengan dos angulos y un lado.
Conocemos tres lados y ningún angulo
En este caso hay que determinar todos y cada uno de los ángulos del triángulo. Para ello se utiliza el teorema del coseno. Por ejemplo, de
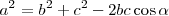
se deduce que
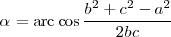
Analogamente, se tiene que:
[Unparseable or potentially dangerous latex formula. Error 3 ]



