Mediana
De Wikillerato
(→Propiedad del baricentro.) |
m (Revertidas las ediciones realizadas por 186.0.34.159 (Talk); a la última edición de Laura.2mdc) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 10: | Línea 10: | ||
Al igual que las demás rectas notables de un triángulo las medianas tienen una propiedad importante. La distancia de un vértice del triángulo al baricentro: punto de corte de las medianas, es siempre el doble que la distancia del baricentro al punto medio del lado opuesto.Expresado de forma más simple el baricentro se encuentra del vértice a una distancia 2/3 de la mediana. | Al igual que las demás rectas notables de un triángulo las medianas tienen una propiedad importante. La distancia de un vértice del triángulo al baricentro: punto de corte de las medianas, es siempre el doble que la distancia del baricentro al punto medio del lado opuesto.Expresado de forma más simple el baricentro se encuentra del vértice a una distancia 2/3 de la mediana. | ||
| + | |||
| + | Naturalmente la propiedad es válida para las 3 medianas. | ||
| + | |||
| + | [[Imagen:bari.jpg]] | ||
[[Categoría:Dibujo]] | [[Categoría:Dibujo]] | ||
Revisión actual
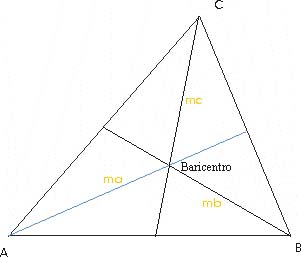
La mediana de un triángulo es el segmento que partiendo de un vértice va hasta el punto medio del lado opuesto. Por tanto un triángulo tiene 3 medianas. Estas rectas llamadas notables se cortan en un punto llamado baricentro. Que coincide con el centro de gravedad del triángulo. Para el trazado geométrico de las medianas es preciso trazar antes las mediatrices de los lados. Se une cada vértice con el punto medio del lado opuesto.
Propiedad del baricentro.
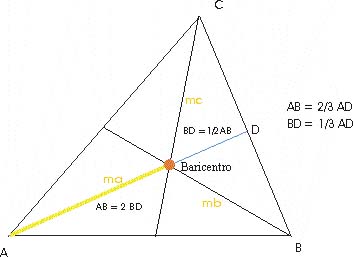
Al igual que las demás rectas notables de un triángulo las medianas tienen una propiedad importante. La distancia de un vértice del triángulo al baricentro: punto de corte de las medianas, es siempre el doble que la distancia del baricentro al punto medio del lado opuesto.Expresado de forma más simple el baricentro se encuentra del vértice a una distancia 2/3 de la mediana.
Naturalmente la propiedad es válida para las 3 medianas.