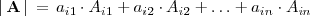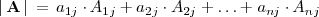Desarrollo de un determinante
De Wikillerato
m (Revertidas las ediciones realizadas por 200.118.90.180 (Talk); a la última edición de Laura.2mdc) |
|||
| (9 ediciones intermedias no se muestran.) | |||
| Línea 215: | Línea 215: | ||
El determinante de una matriz cuadrada de orden <math> n </math> es igual a la suma de los productos de los elementos | El determinante de una matriz cuadrada de orden <math> n </math> es igual a la suma de los productos de los elementos | ||
de una línea o columna cualquiera por sus adjuntos respectivos. Es decir: | de una línea o columna cualquiera por sus adjuntos respectivos. Es decir: | ||
| + | |||
| + | <br/> | ||
| + | |||
<center> | <center> | ||
<math> | <math> | ||
Revisión actual
En esta sección se explica un procedimiento que nos permite calcular determinantes de cualquier orden, pero antes hemos de introducir los conceptos de menor complementario y adjunto.
Menores complementarios y adjuntos
En una matriz cuadrada de orden
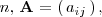 se llama menor complementario del elemento
se llama menor complementario del elemento
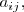 y lo representamos por
y lo representamos por
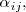 al determinante de la matriz cuadrada de orden
al determinante de la matriz cuadrada de orden
 que resulta de suprimir la fila
que resulta de suprimir la fila
 y la columna
y la columna
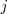 de la matriz
de la matriz

Se llama adjunto del elemento
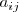 ,
y lo representamos por
,
y lo representamos por
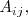 al producto
al producto
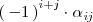 :
:

Ejemplo
Los menores complementarios de la matriz
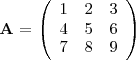
son
![\begin{array}{ccc}
\alpha_{11} =
\left|
</p>
<pre> \begin{array}[c]{cc}
5 & 6
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{12} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 6
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{13} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 5
\\
7 & 8
\end{array}
</pre>
<p>\right|
\\
& &
\\
\alpha_{21} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{22} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{23} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
7 & 8
\end{array}
</pre>
<p>\right|
\end{array}
\begin{array}{ccc}
\alpha_{11} =
\left|
</p>
<pre> \begin{array}[c]{cc}
5 & 6
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{12} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 6
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{13} =
\left|
</p>
<pre> \begin{array}[c]{cc}
4 & 5
\\
7 & 8
\end{array}
</pre>
<p>\right|
\\
& &
\\
\alpha_{21} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
8 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{22} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
7 & 9
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{23} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
7 & 8
\end{array}
</pre>
<p>\right|
\end{array}](/images/math/math-3783e29010f16c31576a73ebc6eb80c8.png)
![\begin{array}[c]{ccc}
\alpha_{31} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
5 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{32} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
4 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{33} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
4 & 5
\end{array}
</pre>
<p>\right|
\end{array}
\begin{array}[c]{ccc}
\alpha_{31} =
\left|
</p>
<pre> \begin{array}[c]{cc}
2 & 3
\\
5 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{32} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 3
\\
4 & 6
\end{array}
</pre>
<p>\right|
&
\qquad \alpha_{33} =
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & 2
\\
4 & 5
\end{array}
</pre>
<p>\right|
\end{array}](/images/math/math-03adb91ef28c3794b095ecb93b73fb77.png)
y sus adjuntos son:
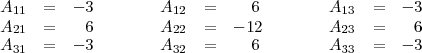
Desarrollo de un determinante
El determinante de una matriz cuadrada de orden  es igual a la suma de los productos de los elementos
de una línea o columna cualquiera por sus adjuntos respectivos. Es decir:
es igual a la suma de los productos de los elementos
de una línea o columna cualquiera por sus adjuntos respectivos. Es decir: