Continuidad de una función
De Wikillerato
(Diferencias entre revisiones)
(→Ejercicios resueltos) |
|||
| Línea 107: | Línea 107: | ||
==Ejercicios resueltos== | ==Ejercicios resueltos== | ||
| - | [http://www. | + | {{problemas}}* [http://www.selectividad.tv/S_M_2_1_16_S_continuidad_y_derivabilidad_de_una_funcion.html Continuidad y derivabilidad de una función] |
| - | + | * [http://www.selectividad.tv/S_M_2_1_2_S_continuidad_y_derivabilidad_de_una_funcion_definida_a_trozos.html Continuidad y derivabilidad de una función definida a trozos] | |
| - | [http://www. | + | |
| - | + | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión actual
Tabla de contenidos |
Definiciones
Una funciónes continua en
si y solo si
.
Una función
 es continua en un intervalo
es continua en un intervalo
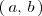 si y solo si
si y solo si
 es continua en
es continua en
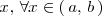 .
.
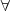 es un simbolo matematico que significa para todo.
es un simbolo matematico que significa para todo.
Se dice que una función
 es continua si y solo si es continua en cada
es continua si y solo si es continua en cada
 de su dominio.
de su dominio.
¿Donde es f continua?
Para determinar si una función
 es continua en
es continua en
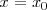 comprobaremos que se verifican todas y cada una de las condiciones siguientes:
comprobaremos que se verifican todas y cada una de las condiciones siguientes:
Condición 1.
Existe 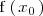 ,
es decir,
,
es decir,  esta en el dominio de
esta en el dominio de  .
.
Condición 2.
Existe 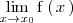 .
.
Condición 3.
Ambos, 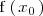 y
y 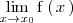 son iguales.
son iguales.
Ejercicios resueltos
También te pueden interesar los siguientes ejercicios resueltos de selectividad
- Continuidad y derivabilidad de una función
- Continuidad y derivabilidad de una función definida a trozos



