Teorema de Rouche-Fröbenius
De Wikillerato
(→Ejemplo:sistemas homogéneos) |
|||
| (5 ediciones intermedias no se muestran.) | |||
| Línea 27: | Línea 27: | ||
| - | ==Ejemplo:sistemas | + | ==Ejemplo:sistemas homogéneos== |
| - | En un sistema de ecuaciones | + | En un sistema de ecuaciones homogéneo, la columna de los términos independientes es nula, de manera que el |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
[[Rango de una matriz|rango]] de la | [[Rango de una matriz|rango]] de la | ||
[[Sistemas de ecuaciones lineales|matriz de los coeficientes]] y el de la | [[Sistemas de ecuaciones lineales|matriz de los coeficientes]] y el de la | ||
[[Sistemas de ecuaciones lineales|matriz ampliada]] coinciden. Esto implica, a su vez, por el teorema de Rouché-Fröbenius, | [[Sistemas de ecuaciones lineales|matriz ampliada]] coinciden. Esto implica, a su vez, por el teorema de Rouché-Fröbenius, | ||
| - | que un sistema | + | que un sistema homogéneo siempre es compatible. En cualquier sistema homogéneo, siempre |
| - | podemos obtener una solución particular igualando todas las | + | podemos obtener una solución particular -llamada solución trivial- igualando todas las incógnitas a 0. |
| - | Un sistema | + | Un sistema homogéneo es compatible indeterminado cuando el número de incógnitas es mayor que el rango de la matriz de coeficientes. |
| - | + | ||
| - | + | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión actual
Este artículo o sección necesita una revisión de gramática, ortografía o estilo.
Cuando se haya corregido, borra esta plantilla, por favor.
Enunciado
|
Si el sistema es compatible, existen dos posibilidades:
- Que el rango de la matriz de los coeficientes sea menor que el numero de incógnitas.
- Que el rango de la matriz de los coeficientes sea igual al numero de incognitas.
En el primer caso el sistema es compatible indeterminado y en el segundo caso el sistema es compatible determinado.
Ejemplo:sistemas homogéneos
En un sistema de ecuaciones homogéneo, la columna de los términos independientes es nula, de manera que el rango de la matriz de los coeficientes y el de la matriz ampliada coinciden. Esto implica, a su vez, por el teorema de Rouché-Fröbenius, que un sistema homogéneo siempre es compatible. En cualquier sistema homogéneo, siempre podemos obtener una solución particular -llamada solución trivial- igualando todas las incógnitas a 0.



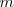 ecuaciones lineales con
ecuaciones lineales con
 incógnitas es compatible (tiene solución) si, y sólo si, el
incógnitas es compatible (tiene solución) si, y sólo si, el 
