Curvas técnicas
De Wikillerato
(→Espirales, volutas y evolventes) |
|||
| (58 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | {{protegida}} | ||
{{en desarrollo}} | {{en desarrollo}} | ||
| + | |||
===Concepto de curva técnica=== | ===Concepto de curva técnica=== | ||
| Línea 31: | Línea 33: | ||
[[Imagen:43-2-Curvastecnicas.gif]] | [[Imagen:43-2-Curvastecnicas.gif]] | ||
| + | <h3>Enlaces externos</h3> | ||
| + | |||
| + | :[http://trazoide.com/otros_temas.html TRAZOIDE. Teoría y ejercicios resueltos sobre CURVAS TÉCNICAS en Dibujo Técnico] | ||
[[Categoría:Dibujo]] | [[Categoría:Dibujo]] | ||
Revisión actual
Esta página ha sido protegida
Esto puede deberse a que ha sido objeto de vandalismo o a que existe una discusión abierta sobre su contenido. La protección no implica necesariamente el respaldo a la edición actual.
Uno o más usuarios están trabajando actualmente en extender este artículo.
Es posible que, a causa de ello, haya lagunas de contenido o deficiencias de formato. Por favor, antes de realizar correcciones mayores o reescrituras, contacta con ellos en la página de discusión.
Tabla de contenidos |
Concepto de curva técnica
Son curvas de aplicación en la ingeniería y en la arquitectura.
Óvalos y ovoides
Son curvas técnicas formadas por circunferencias tangentes entre sí: con forma de huevo (ovoides) o con forma parecida a la de las elipses (óvalos).
En la figura vemos un óvalo inscrito en un rombo.
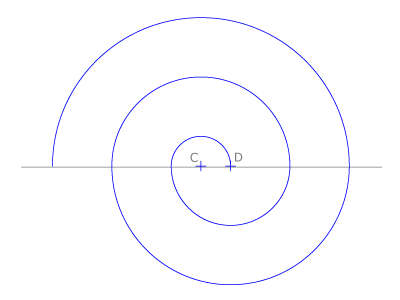
Espirales, volutas y evolventes
Son curvas técnicas, engendradas por un punto que se aleja o se acerca a su origen según se mueva en uno u otro sentido. Algunas están formadas por arcos de circunferencia (como las espirales de centros alineados, las de centros en los vértices de polígonos, regulares o no, las volutas y las espirales áurea y logarítmica). Otras espirales son representaciones de trayectorias, como la espiral de Arquímedes y la evolvente de la circunferencia.
En la figura vemos la espiral más sencilla, la de Honnecourt, con dos centros.
Curvas cíclicas
Son representaciones de trayectorias que se repiten una vez cumplido su ciclo. Por ejemplo, la cicloide es la trayectoria de un punto fijo sobre una circunferencia que se desplaza en línea recta, recorriendo espacios iguales en tiempos iguales.
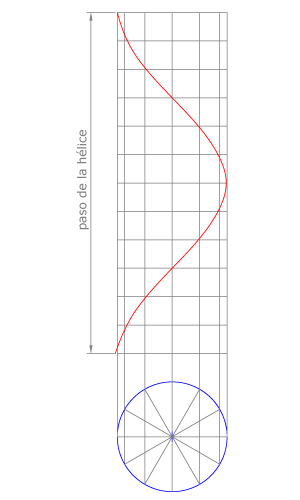
Otras curvas
La hélice cilíndrica, que no es una curva plana, también se estudia por ser de gran aplicación en arquitectura (escaleras de caracol) y en ingeniería (formas helicoidales).