Navegación
Ley de Hooke
De Wikillerato
m (Revertidas las ediciones realizadas por 83.58.134.190 (Talk); a la última edición de 213.97.196.225) |
|||
| (26 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | Recordemos brevemente la Ley de Hooke, que sirve, por ejemplo, para hacer el calibrado de un dinamómetro. | + | Recordemos brevemente la '''Ley de Hooke''', que sirve, por ejemplo, para hacer el calibrado de un dinamómetro. |
| - | Si suspendemos de un resorte una m y la soltamos, ésta comienza a oscilar hasta que alcanza el equilibrio. Es decir, la masa se detiene cuando la suma de las fuerzas aplicadas sobre la masa es cero. | + | Si suspendemos de un resorte una masa <math>m</math> y la soltamos, ésta comienza a oscilar hasta que alcanza el equilibrio. Es decir, la masa se detiene cuando la suma de las fuerzas aplicadas sobre la masa es cero. |
| - | + | <div>[[Imagen:Leyhooke.gif]]</div> | |
| - | <math> \vec F + m\vec g = 0</math> | + | Cuando se ha alcanzado el equilibrio la fuerza recuperadora del resorte <math>F</math> será una fuerza de módulo igual al peso, <math>mg</math>, pero tendrá sentido contrario. |
| + | |||
| + | <math> \vec F + m\vec g = 0.</math> | ||
Pero en cada instante, la fuerza es directamente proporcional a la deformación que sufre el resorte. De un modo general podremos escribir: | Pero en cada instante, la fuerza es directamente proporcional a la deformación que sufre el resorte. De un modo general podremos escribir: | ||
| - | <math>\vec F = - k (x | + | <math>\vec F = - k (\vec x - \vec x_0) \,</math> ''Ley de Hooke'' |
| + | |||
| + | Donde <math> F</math> es la fuerza recuperadora que ejerce el resorte debido a la deformación <math>\Delta x = x - x_o </math> y <math>k</math> es la constante de elasticidad del resorte. | ||
| + | |||
| + | La constante de elasticidad <math>k</math>, es una característica del mismo, depende sólo de la forma del resorte y del material con que se ha construido. Debe ponerse el signo menos dado que el sentido de <math>F</math>, como se ve en la ilustración, será siempre el opuesto al de la deformación <math>\Delta x</math>. | ||
| + | |||
| + | [[Experiencia para obtener la Ley de Hooke| Tema avanzado: Experiencia para obtener la Ley de Hooke]] | ||
| + | |||
| + | Si una vez alcanzado el equilibrio, es decir cuando <math> \vec F + m \vec g = 0 </math>, tiramos de <math>m</math>, produciendo en el resorte un alargamiento suplementario <math>A</math>, con relación a la posición de equilibrio, y dejamos el sistema en libertad, observaremos que el resorte comienza a oscilar alrededor de la posición de equilibrio <math> O </math>, repitiéndose periódicamente su posición con respecto a <math> O </math>. Un movimiento de estas características es denominado movimiento oscilatorio armónico o movimiento armónico simple. | ||
| + | |||
| + | El movimiento se inicia porque al deformar el resorte (estirarlo o comprimirlo) le aportamos una energía que el resorte desarrolla al dejarlo en libertad. Esta energía será una energía potencial, puesto que la definición que hemos dado de ésta siempre ha sido la capacidad del sistema para desarrollar un trabajo. Veamos cuál es en el sistema que estudiamos. | ||
| + | |||
| + | No debe dejar de observarse que el peso de <math>m</math>, <math>m \vec g</math> es constante, es decir mantiene su módulo, dirección -la vertical- y sentido -hacia abajo-. | ||
| - | + | Sin embargo la fuerza recuperadora cambia constantemente de módulo, e invierte su sentido cuando pasa por el punto de equilibrio, y siempre en sentido opuesto a la deformación. | |
| - | + | [[Categoría:Física|Hooke]] | |
Revisión actual
Recordemos brevemente la Ley de Hooke, que sirve, por ejemplo, para hacer el calibrado de un dinamómetro.
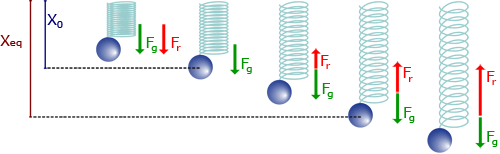
Si suspendemos de un resorte una masa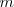 
y la soltamos, ésta comienza a oscilar hasta que alcanza el equilibrio. Es decir, la masa se detiene cuando la suma de las fuerzas aplicadas sobre la masa es cero.
Cuando se ha alcanzado el equilibrio la fuerza recuperadora del resorte 
será una fuerza de módulo igual al peso,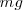 
, pero tendrá sentido contrario.
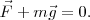
Pero en cada instante, la fuerza es directamente proporcional a la deformación que sufre el resorte. De un modo general podremos escribir:
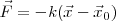Ley de Hooke
Donde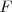 
es la fuerza recuperadora que ejerce el resorte debido a la deformación 
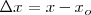y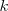 
es la constante de elasticidad del resorte.
La constante de elasticidad 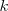, es una característica del mismo, depende sólo de la forma del resorte y del material con que se ha construido. Debe ponerse el signo menos dado que el sentido de , como se ve en la ilustración, será siempre el opuesto al de la deformación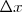 
.
Tema avanzado: Experiencia para obtener la Ley de Hooke
Si una vez alcanzado el equilibrio, es decir cuando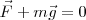 
, tiramos de 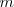, produciendo en el resorte un alargamiento suplementario 
, con relación a la posición de equilibrio, y dejamos el sistema en libertad, observaremos que el resorte comienza a oscilar alrededor de la posición de equilibrio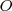 
, repitiéndose periódicamente su posición con respecto a 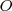. Un movimiento de estas características es denominado movimiento oscilatorio armónico o movimiento armónico simple.
El movimiento se inicia porque al deformar el resorte (estirarlo o comprimirlo) le aportamos una energía que el resorte desarrolla al dejarlo en libertad. Esta energía será una energía potencial, puesto que la definición que hemos dado de ésta siempre ha sido la capacidad del sistema para desarrollar un trabajo. Veamos cuál es en el sistema que estudiamos.
No debe dejar de observarse que el peso de ,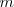 
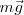es constante, es decir mantiene su módulo, dirección -la vertical- y sentido -hacia abajo-.
Sin embargo la fuerza recuperadora cambia constantemente de módulo, e invierte su sentido cuando pasa por el punto de equilibrio, y siempre en sentido opuesto a la deformación.
Tweet
