Navegación
Concavidad y convexidad
De Wikillerato
(→Concava) |
|||
| (7 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | == | + | ==Convexidad== |
<br/> | <br/> | ||
| Línea 40: | Línea 40: | ||
<br/> | <br/> | ||
| - | == | + | ==Concavidad== |
<br/> | <br/> | ||
| Línea 64: | Línea 64: | ||
\mathrm{f} | \mathrm{f} | ||
</math> | </math> | ||
| - | es ''''' | + | es '''''cóncava''''' en |
<math> | <math> | ||
a | a | ||
| Línea 85: | Línea 85: | ||
<br/> | <br/> | ||
| - | Un '''''punto de inflexion''''' es un punto donde la función pasa de ser | + | Un '''''punto de inflexion''''' es un punto donde la función pasa de ser cóncava a convexa o viceversa. |
<br/> | <br/> | ||
Revisión actual
Tabla de contenidos[ocultar] |
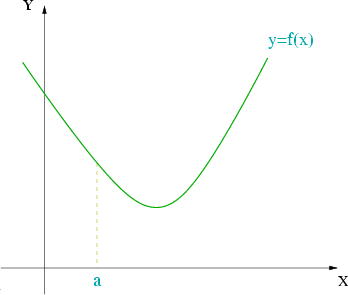
Convexidad
Si la derivada segunda de
en
es positiva, entonces
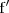es creciente en
y
es convexa en
.
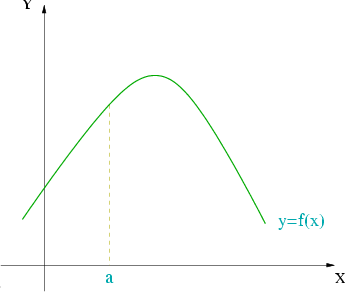
Concavidad
Si la derivada segunda de
en
es negativa, entonces
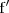es decreciente en
y
es cóncava en
.
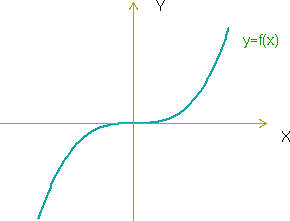
Puntos de inflexión
Un punto de inflexion es un punto donde la función pasa de ser cóncava a convexa o viceversa.
La función cuya grafica se muestra en la figura de abajo tiene un punto de inflexión en el origen de coordenadas ( intersección de los ejes X e Y ).
Si
es un punto de inflexión de
, entonces
,
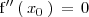pero lo reciproco no es cierto en general:
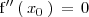no implica que
sea un punto de inflexión de
.
Ejemplo
La derivada segunda de la función
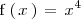se anula en
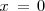pero
no tiene un punto de inflexión en el punto de abcisa
.
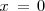es covexa en todo su dominio ( R ).
Ejemplo
La derivada segunda de la función
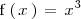se anula en
.
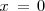tiene un punto de inflexión en el punto de abcisa
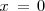porque
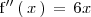cambia de signo en
:
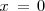si
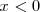entonces
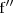es negativa (
es concava ) y si
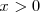entonces
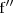es positiva (
es convexa ).
Tweet
