Posiciones relativas de recta y plano
De Wikillerato
(→Introduccion) |
(→Secantes: Rango ( A ) = Rango ( A | B ) = 3) |
||
| (28 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| + | {{revisar}} | ||
| + | |||
==Introduccion== | ==Introduccion== | ||
| Línea 85: | Línea 87: | ||
<br/> | <br/> | ||
| + | Es una linia que divide uns circumferencia en dos partes. | ||
===Paralelos: Rango ( A ) = 2, Rango ( A | B ) = 3=== | ===Paralelos: Rango ( A ) = 2, Rango ( A | B ) = 3=== | ||
| Línea 126: | Línea 129: | ||
Dependiendo de si este sistema tuviese una, ninguna o mas de una solucion estariamos en | Dependiendo de si este sistema tuviese una, ninguna o mas de una solucion estariamos en | ||
el primer, segundo o tercer caso discutidos arriba, respectivamente. | el primer, segundo o tercer caso discutidos arriba, respectivamente. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ====Ejemplo==== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para hallar la interseccion del plano | ||
| + | <math> | ||
| + | \pi | ||
| + | </math> | ||
| + | de ecuacion: | ||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \, x = 1 | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | con la recta | ||
| + | <math> | ||
| + | r | ||
| + | </math> | ||
| + | de ecuacion: | ||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left\{ | ||
| + | \begin{array}[c]{rcl} | ||
| + | x & = & 1 \, + \, \alpha | ||
| + | \\ | ||
| + | y & = & 2 \, + \, \alpha | ||
| + | \\ | ||
| + | z & = & 3 \, + \, \alpha | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Resolvemos el sistema de ecuaciones: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left\{ | ||
| + | \begin{array}[c]{rcl} | ||
| + | x & = & 1 | ||
| + | \\ | ||
| + | x & = & 1 \, + \, \alpha | ||
| + | \\ | ||
| + | y & = & 2 \, + \, \alpha | ||
| + | \\ | ||
| + | z & = & 3 \, + \, \alpha | ||
| + | \end{array} | ||
| + | \right. | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Como la solucion de este sistema de ecuaciones es unica: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \, x, \, y, \, z \, | ||
| + | \right) | ||
| + | = | ||
| + | \left( | ||
| + | \, 1, \, 2, \, 3 \, | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | este es el unico punto comun a la recta | ||
| + | <math> | ||
| + | r | ||
| + | </math> | ||
| + | y al plano | ||
| + | <math> | ||
| + | \pi | ||
| + | </math> | ||
| + | y por tanto | ||
| + | <math> | ||
| + | r | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | \pi | ||
| + | </math> | ||
| + | son secantes. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ---- | ||
<br/> | <br/> | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión actual
Este artículo o sección necesita una revisión de gramática, ortografía o estilo.
Cuando se haya corregido, borra esta plantilla, por favor.
Tabla de contenidos |
Introduccion
Una recta y un plano pueden adoptar en el espacio estas tres posiciones relativas:
1. Secantes.
2. Paralelos.
3. Recta contenida en el plano.
Supongamos que la recta
 viene dada como la interseccion de dos planos
viene dada como la interseccion de dos planos
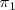 y
y
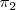
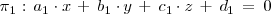
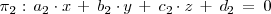
y supongamos que queremos determinar su posicion relativa en el espacio con respecto al
plano
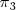
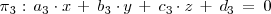
Según el teorema de Rouché-Frobenius, se pueden los siguientes casos que pasamos a describir en la seccion siguiente.
Casos que se pueden dar:
Secantes: Rango ( A ) = Rango ( A | B ) = 3
El sistema de ecuaciones es compatible determinado, tiene una unica solución. La recta y el plano tienen un punto en común. La recta y el plano son secantes.
Es una linia que divide uns circumferencia en dos partes.
Paralelos: Rango ( A ) = 2, Rango ( A | B ) = 3
El sistema de ecuaciones es incompatible, no tiene solucion. La recta y el plano no tienen ningún punto en común. La recta y el plano son paralelos.
Recta contenida en el plano: Rango ( A ) = Rango ( A | B ) = 2
El sistema de ecuaciones es compatible indeterminado, tiene infinitas soluciones. Todos los puntos de la recta son solucion del sistema. La recta está contenida en el plano.
Suponiendo que tuviesemos la ecuación de la recta dada en forma parametrica en vez de venir dada como la intersección de dos planos, entonces, juntando las ecuaciones de la recta con la del plano, obtendriamos un sistema de cuatro ecuciones con cuatro incognitas. Estas ultimas serian:
- las coordenadas del punto de interseccion y
- el parametro que aparece en las ecuaciones de la recta.
Dependiendo de si este sistema tuviese una, ninguna o mas de una solucion estariamos en el primer, segundo o tercer caso discutidos arriba, respectivamente.
Ejemplo
Para hallar la interseccion del plano
 de ecuacion:
de ecuacion:
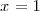
con la recta
 de ecuacion:
de ecuacion:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x & = & 1 \, + \, \alpha
\\
y & = & 2 \, + \, \alpha
\\
z & = & 3 \, + \, \alpha
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x & = & 1 \, + \, \alpha
\\
y & = & 2 \, + \, \alpha
\\
z & = & 3 \, + \, \alpha
\end{array}
</pre>
<p>\right.](/images/math/math-7dbb9c28742b8a51f8bb9f46a8c470e4.png)
Resolvemos el sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x & = & 1
\\
x & = & 1 \, + \, \alpha
\\
y & = & 2 \, + \, \alpha
\\
z & = & 3 \, + \, \alpha
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
x & = & 1
\\
x & = & 1 \, + \, \alpha
\\
y & = & 2 \, + \, \alpha
\\
z & = & 3 \, + \, \alpha
\end{array}
</pre>
<p>\right.](/images/math/math-9f4836a125b0496208aa60b3931533ab.png)
Como la solucion de este sistema de ecuaciones es unica:
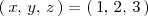
este es el unico punto comun a la recta
 y al plano
y al plano
 y por tanto
y por tanto
 y
y
 son secantes.
son secantes.



