Experimentos aleatorios. Espacio muestral.Sucesos
De Wikillerato
(→1. ExPeRiMeNtO aLeAtOrIo) |
|||
| Línea 1: | Línea 1: | ||
| - | ==1. | + | ==1. El concepto de número== |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| + | Un número es una entidad abstracta que representa una cantidad (de una magnitud). El símbolo de un número recibe el nombre de numeral o cifra. Los números se usan en la vida diaria como etiquetas (números de teléfono, numeración de carreteras), como indicadores de orden (números de serie), como códigos (ISBN), etc. En matemática, la definición de número se extiende para incluir abstracciones tales como números fraccionarios, negativos, irracionales, trascendentales y complejos. | ||
<br/> | <br/> | ||
| - | |||
| - | ==2. | + | ==2. Tipos de números== |
| - | + | Los números más conocidos son los '''números naturales''', que se usan para contar. Éstos, conjuntamente con los números negativos, conforman el conjunto de los '''números enteros'''. Al realizar divisiones o cocientes de números enteros generan los '''números racionales'''. Si se incluyen todos los números que pueden expresarse con decimales pero no con fracciones de enteros (irracionales), se habla entonces de los '''números reales'''; si a éstos se les añade los '''números complejos''', se obtendrán todos los números necesarios para resolver cualquier ecuación algebraica. Pueden añadirse también los infinitos, los hiperreales y los transfinitos. Entre los reales, existen números que no son soluciones de una ecuación polinomial o algebraica, que reciben el nombre de transcendentales. Ejemplos famosos de estos números son el número π (Pi) y el número e (este último base de los logaritmos naturales), los cuales están relacionados entre sí por la identidad de Euler. | |
| - | |||
| - | |||
<math> | <math> | ||
| - | + | \begin{array}{ll} | |
| + | \mathbb{C} & \mbox{Complejos} | ||
| + | \begin{cases} | ||
| + | \mathbb{R} & \mbox{Reales} | ||
| + | \begin{cases} | ||
| + | \mathbb{Q} & \mbox{Racionales} | ||
| + | \begin{cases} | ||
| + | \mathbb{Z} & \mbox{Enteros} | ||
| + | \begin{cases} | ||
| + | \mathbb{N} & \mbox{Naturales} \\ | ||
| + | & \mbox{Cero} \\ | ||
| + | & \mbox{Enteros negativos} | ||
| + | \end{cases}\\ | ||
| + | & \mbox{Fraccionarios} | ||
| + | \end{cases}\\ | ||
| + | & \mbox{Irracionales} | ||
| + | \end{cases}\\ | ||
| + | \mathbb{I} & \mbox{Imaginarios} | ||
| + | \end{cases} | ||
| + | \end{array} | ||
</math> | </math> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
[[Categoría:Matemáticas]] | [[Categoría:Matemáticas]] | ||
Revisión de 11:53 3 jul 2011
1. El concepto de número
Un número es una entidad abstracta que representa una cantidad (de una magnitud). El símbolo de un número recibe el nombre de numeral o cifra. Los números se usan en la vida diaria como etiquetas (números de teléfono, numeración de carreteras), como indicadores de orden (números de serie), como códigos (ISBN), etc. En matemática, la definición de número se extiende para incluir abstracciones tales como números fraccionarios, negativos, irracionales, trascendentales y complejos.
2. Tipos de números
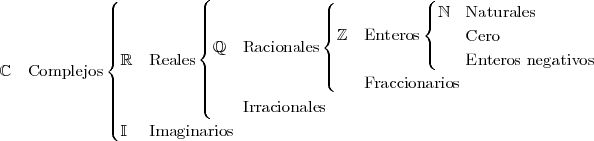
Los números más conocidos son los números naturales, que se usan para contar. Éstos, conjuntamente con los números negativos, conforman el conjunto de los números enteros. Al realizar divisiones o cocientes de números enteros generan los números racionales. Si se incluyen todos los números que pueden expresarse con decimales pero no con fracciones de enteros (irracionales), se habla entonces de los números reales; si a éstos se les añade los números complejos, se obtendrán todos los números necesarios para resolver cualquier ecuación algebraica. Pueden añadirse también los infinitos, los hiperreales y los transfinitos. Entre los reales, existen números que no son soluciones de una ecuación polinomial o algebraica, que reciben el nombre de transcendentales. Ejemplos famosos de estos números son el número π (Pi) y el número e (este último base de los logaritmos naturales), los cuales están relacionados entre sí por la identidad de Euler.