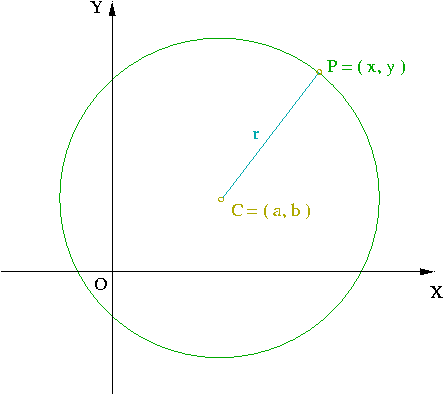Circunferencia
De Wikillerato
| (17 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | |||
| - | |||
==Definición== | ==Definición== | ||
| - | + | Llamamos '''''lugar geométrico''''' al conjunto de puntos que satisfacen una determinada propiedad. | |
| - | + | Una '''''circunferencia''''' es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. | |
| - | + | ||
| - | + | La distancia de cualquier punto de la circunferencia al centro se llama '''radio'''. | |
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
==Ecuación== | ==Ecuación== | ||
| - | + | Para obtener la ecuación de la circunferencia consideramos un sistema de referencia ortonormal en el plano (con sus ejes de coordenadas y origen). | |
| - | + | ||
| - | Para obtener la ecuación de la circunferencia consideramos un sistema de referencia | + | |
| - | ortonormal en el plano ( con sus ejes de coordenadas y origen ). | + | |
<br/> | <br/> | ||
| Línea 213: | Línea 199: | ||
</center> | </center> | ||
| - | + | ==Enlaces externos== | |
| + | # "[http://trazoide.com/circunferencias_y_arcos.html TRAZOIDE. Teoría y ejercicios resueltos de CIRCUNFERENCIAS y ARCOS en Dibujo Técnico]" | ||
| + | # ''[http://www.vadenumeros.es/primero/conicas-circunferencia-y-elipse.htm Cónicas: Ecuaciones de la circunferencia y la elipse]'', Pilar Ferrero Casado. Matemáticas: ESO, Bachillerato y Selectividad. | ||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
| + | [[Categoría:Dibujo]] | ||
Revisión actual
Tabla de contenidos |
Definición
Llamamos lugar geométrico al conjunto de puntos que satisfacen una determinada propiedad.
Una circunferencia es el lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro.
La distancia de cualquier punto de la circunferencia al centro se llama radio.
Ecuación
Para obtener la ecuación de la circunferencia consideramos un sistema de referencia ortonormal en el plano (con sus ejes de coordenadas y origen).
Si
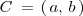 es el centro de la circunferencia de radio
es el centro de la circunferencia de radio
 y
y
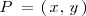 es un punto cualquiera de ella, entonces se verifica que la distancia de
es un punto cualquiera de ella, entonces se verifica que la distancia de
 a
a
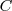 es
es
 , por tanto:
, por tanto:
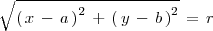
Elevando al cuadrado, obtenemos la ecuación de la circunferencia:
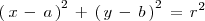
Ejemplo
Supongamos que nos dan la siguiente ecuación de una circunferencia:
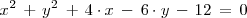
y nos piden calcular el radio y el centro de la misma. Como hemos visto anteriormente, la
ecuación de una circunferencia de centro
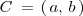 y radio
y radio
 se puede escribir de la forma:
se puede escribir de la forma:
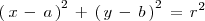
Si pasamos
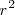 al otro lado del signo igual, desarrollamos los cuadrados y agrupamos los terminos
independientes obtenemos:
al otro lado del signo igual, desarrollamos los cuadrados y agrupamos los terminos
independientes obtenemos:
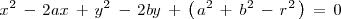
Comparando esta ecuación con la que nos dan e igualando coeficientes, obtenemos:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
-2a & = & 4
\\
-2b & = & -6
\\
a^2 \, + \, b^2 \, - \, r^2 & = & -12
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
-2a & = & 4
\\
-2b & = & -6
\\
a^2 \, + \, b^2 \, - \, r^2 & = & -12
\end{array}
</pre>
<p>\right.](/images/math/math-a87991b7e16986f52c2513b6aaaa50eb.png)
de donde se deduce que
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
a & = & -2
\\
b & = & 3
\\
r & = & 5
\end{array}
</pre>
<p>\right.
\left\{
</p>
<pre> \begin{array}[c]{rcl}
a & = & -2
\\
b & = & 3
\\
r & = & 5
\end{array}
</pre>
<p>\right.](/images/math/math-762fc79be6e08260735a358d22e23d0a.png)
Enlaces externos
- "TRAZOIDE. Teoría y ejercicios resueltos de CIRCUNFERENCIAS y ARCOS en Dibujo Técnico"
- Cónicas: Ecuaciones de la circunferencia y la elipse, Pilar Ferrero Casado. Matemáticas: ESO, Bachillerato y Selectividad.