Conceptos básicos: espacios vectoriales
De Wikillerato
(→Definición de espacio vectorial) |
|||
| Línea 1: | Línea 1: | ||
| - | En el plano, un vector fijo | + | En el plano, un vector fijo |
| - | orientado de origen | + | <math> |
| - | caracteristicas: | + | \stackrel{\longrightarrow}{PQ} |
| + | </math> | ||
| + | es un segmento orientado de origen | ||
| + | <math> | ||
| + | P | ||
| + | </math> | ||
| + | y extremo | ||
| + | <math> | ||
| + | Q | ||
| + | </math> | ||
| + | , que tiene las siguientes caracteristicas: | ||
<br/> | <br/> | ||
| - | <math> \bullet </math> Módulo: longitud del segmento | + | <math> |
| + | \bullet | ||
| + | </math> | ||
| + | Módulo: longitud del segmento | ||
| + | <math> | ||
| + | PQ | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | <math> \bullet </math> Dirección: la de la recta que lo contiene y todas sus paralelas. | + | <math> |
| + | \bullet | ||
| + | </math> | ||
| + | Dirección: la de la recta que lo contiene y todas sus paralelas. | ||
<br/> | <br/> | ||
| - | <math> \bullet </math> Sentido: el que va del origen al extremo. | + | <math> |
| + | \bullet | ||
| + | </math> | ||
| + | Sentido: el que va del origen al extremo. | ||
<br/> | <br/> | ||
| - | Los vectores | + | Los vectores |
| - | </math> | + | <math> |
| - | <math> \stackrel{\ | + | \stackrel{\longrightarrow}{PQ} |
| - | </math> | + | </math> |
| + | y | ||
| + | <math> | ||
| + | \stackrel{\longrightarrow}{QP} | ||
| + | </math> | ||
| + | tienen el mismo módulo y la misma dirección, pero sentido contrario. | ||
| + | Los vectores | ||
| + | <math> | ||
| + | \stackrel{\longrightarrow}{PQ} | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | \stackrel{\longrightarrow}{QP} | ||
| + | </math> | ||
| + | son opuestos. | ||
<br/> | <br/> | ||
| Línea 26: | Línea 62: | ||
El conjunto de todos los vectores fijos del mismo módulo, dirección y sentido forma lo | El conjunto de todos los vectores fijos del mismo módulo, dirección y sentido forma lo | ||
que se denomina un vector libre. Una propiedad importante que cumplen los vectores libres | que se denomina un vector libre. Una propiedad importante que cumplen los vectores libres | ||
| - | es que si | + | es que si |
| - | existe un único punto | + | <math> |
| + | \vec{u} | ||
| + | </math> | ||
| + | es un vector libre y | ||
| + | <math> | ||
| + | O | ||
| + | </math> | ||
| + | es un punto del plano, existe un único punto | ||
| + | <math> | ||
| + | P | ||
| + | </math> tal que | ||
| + | <math> | ||
| + | \vec{u} \, = \, \stackrel{\longrightarrow}{OP} | ||
| + | </math>. | ||
<br/> | <br/> | ||
| - | + | ==Componentes de un vector== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | Para representar un punto | + | Un sistema de referencia esta formado por dos rectas |
| - | se trazan dese | + | <math> |
| - | P_2 </math>. | + | OX |
| - | P_2 </math> | + | </math> |
| - | el nombre de coordenadas del punto | + | y |
| + | <math> | ||
| + | OY | ||
| + | </math> | ||
| + | , llamadas ejes de coordenadas que se cortan en un punto | ||
| + | <math> | ||
| + | O | ||
| + | </math> | ||
| + | , origen de coordenadas, y una unidad de medida en cada eje. Cuando las dos rectas | ||
| + | son perpendiculares el sistema es ortogonal y cuando, además, las dos unidades de medida | ||
| + | son iguales a uno, el sistema es ortonormal. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Para representar un punto | ||
| + | <math> | ||
| + | P | ||
| + | </math> | ||
| + | del plano en un sistema de coordenadas cartesiano | ||
| + | se trazan dese | ||
| + | <math> | ||
| + | P | ||
| + | </math> | ||
| + | perpendiculares a los ejes, obteniendo | ||
| + | <math> | ||
| + | P_1 | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | P_2 | ||
| + | </math> | ||
| + | . Si la distancia de | ||
| + | <math> | ||
| + | P_1 | ||
| + | </math> | ||
| + | a | ||
| + | <math> | ||
| + | O | ||
| + | </math> | ||
| + | es | ||
| + | <math> | ||
| + | x_1 | ||
| + | </math> | ||
| + | , y la de | ||
| + | <math> | ||
| + | P_2 | ||
| + | </math> | ||
| + | a | ||
| + | <math> | ||
| + | O | ||
| + | </math> | ||
| + | es | ||
| + | <math> | ||
| + | y_1 | ||
| + | </math> | ||
| + | , entonces | ||
| + | <math> | ||
| + | x_1 | ||
| + | </math> | ||
| + | e | ||
| + | <math> | ||
| + | y_1 | ||
| + | </math> | ||
| + | reciben el nombre de coordenadas del punto | ||
| + | <math> | ||
| + | P | ||
| + | </math> | ||
| + | . Se escribe | ||
<math> | <math> | ||
P = | P = | ||
\left( | \left( | ||
| - | + | \, x_1, \, y_1 \, | |
\right) | \right) | ||
</math> | </math> | ||
| - | , | + | , siendo |
| + | <math> | ||
| + | x_1 | ||
| + | </math> | ||
| + | la abcisa e | ||
| + | <math> | ||
| + | y_1 | ||
| + | </math> | ||
| + | la ordenada. | ||
<br/> | <br/> | ||
| - | Conocidas las coordenadas del origen | + | Conocidas las coordenadas del origen |
<math> | <math> | ||
A = | A = | ||
\left( | \left( | ||
| - | \, x_1, \, y_1 \, | + | \, x_1, \, y_1 \, |
\right) | \right) | ||
</math> | </math> | ||
| - | + | y del extremo | |
<math> | <math> | ||
B = | B = | ||
\left( | \left( | ||
| - | + | \, x_2, \, y_2 \, | |
\right) | \right) | ||
</math> | </math> | ||
| - | \, de un vector | + | de un vector fijo |
| + | <math> | ||
| + | \stackrel{\longrightarrow}{AB} | ||
| + | </math> | ||
| + | , se puede determinar las componentes del vector restando a las coordenadas del | ||
| + | extremo las del origen: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \stackrel{\longrightarrow}{AB} = | ||
| + | \left( | ||
| + | \, x_2 - x_1, \, y_2 - y_1 \, | ||
| + | \right) | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Suma de vectores== | ||
| + | |||
| + | <br/> | ||
| + | |||
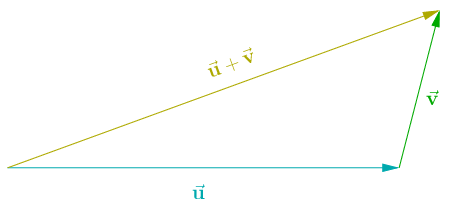
| + | Sean | ||
| + | <math> | ||
| + | \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | y | ||
| + | <math> | ||
| + | \vec{\mathbf{v}} | ||
| + | </math> | ||
| + | dos vectores libres, se define el vector suma | ||
| + | <math> | ||
| + | \vec{\mathbf{u}} + \vec{\mathbf{v}} | ||
| + | </math> | ||
| + | como otro vector obtenido de la siguiente forma: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 1. Se señala un punto | ||
| + | <math> | ||
| + | O | ||
| + | </math> | ||
| + | del plano y se traza el vector | ||
| + | <math> | ||
| + | \stackrel{\longrightarrow}{OP} | ||
| + | </math> | ||
| + | representante de | ||
| + | <math> | ||
| + | \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | . | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 2. Por el extremo | ||
| + | <math> | ||
| + | P | ||
| + | </math> | ||
| + | se traza el vector | ||
| + | <math> | ||
| + | \stackrel{\longrightarrow}{PQ} | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | 3. El vector | ||
| + | <math> | ||
| + | \stackrel{\longrightarrow}{OQ} | ||
| + | </math> | ||
| + | que tiene como origen | ||
| + | <math> | ||
| + | O | ||
| + | </math> | ||
| + | ( origen del primero ) y como extremo | ||
| + | <math> | ||
| + | Q | ||
| + | </math> | ||
| + | ( extremo del segundo ) es el representante del vector suma | ||
| + | <math> | ||
| + | \vec{u} + \vec{v} | ||
| + | </math> | ||
| + | . | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | [[Imagen:sumaVectores.gif]] | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La suma tiene las siguientes '''propiedades''': | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | $ \bullet $ | ||
| + | </math> | ||
| + | Asosiativa: | ||
| + | <math> | ||
| + | \left( | ||
| + | \, \vec{\mathbf{u}} + \vec{\mathbf{v}} \, | ||
| + | \right) | ||
| + | + \vec{\mathbf{w}} = | ||
| + | \vec{\mathbf{u}} + | ||
| + | \left( | ||
| + | \, \vec{\mathbf{v}} + \vec{\mathbf{w}} \, | ||
| + | \right) | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | $ \bullet $ | ||
| + | </math> | ||
| + | El vector nulo es | ||
| + | <math> | ||
| + | \vec{\mathbf{0}} | ||
| + | </math> | ||
| + | , pues: | ||
| + | <math> | ||
| + | \vec{\mathbf{u}} + \vec{\mathbf{0}} = \vec{\mathbf{0}} + \vec{\mathbf{u}} = | ||
| + | \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | $ \bullet $ | ||
| + | </math> | ||
| + | El vector opuesto de | ||
| + | <math> | ||
| + | \vec{\mathbf{v}} | ||
| + | </math> | ||
| + | es | ||
| + | <math> | ||
| + | -\vec{\mathbf{v}} | ||
| + | </math> | ||
| + | , pues: | ||
| + | <math> | ||
| + | \vec{\mathbf{u}} + \left( -\vec{\mathbf{u}} \right) = \left( -\vec{\mathbf{u}} \right) + | ||
| + | \vec{\mathbf{u}} = \vec{\mathbf{0}} | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <math> | ||
| + | $ \bullet $ | ||
| + | </math> | ||
| + | Conmutativa: | ||
| + | <math> | ||
| + | \vec{\mathbf{u}} + \vec{\mathbf{v}} = \vec{\mathbf{v}} + \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==Producto de un número real por un vector== | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Si | ||
| + | <math> | ||
| + | \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | es un vector libre y | ||
| + | <math> | ||
| + | \alpha | ||
| + | </math> | ||
| + | un número real, se define el producto | ||
| + | <math> | ||
| + | \alpha \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | como un nuevo vector qu tiene por módulo el producto | ||
| + | <math> | ||
| + | \left| \, \alpha \, \right| \cdot \left| \, \vec{\mathbf{u}} \, \right| | ||
| + | </math> | ||
| + | , por dirección la misma de | ||
| + | <math> | ||
| + | \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | y sentido el mismo de | ||
| + | <math> | ||
| + | \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | si | ||
| + | <math> | ||
| + | \alpha | ||
| + | </math> | ||
| + | es positivo, y opuesto, si | ||
| + | <math> | ||
| + | \alpha | ||
| + | </math> | ||
| + | es negativo. | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | [[Imagen:numeroPorVector]] | ||
| + | |||
| + | El producto de un número real por un vector tiene las siguientes propiedades: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \alpha | ||
| + | \left( | ||
| + | \, \vec{\mathbf{u}} + \vec{\mathbf{v}} \, | ||
| + | \right) | ||
| + | = \alpha \vec{\mathbf{u}} + \alpha \mathbf{v} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \left( | ||
| + | \, \alpha + \mu \, | ||
| + | \right) | ||
| + | \vec{\mathbf{u}} | ||
| + | = \alpha \vec{\mathbf{u}} + \mu \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | 1 \cdot \vec{\mathbf{u}} = \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | \alpha | ||
| + | \left( | ||
| + | \, \mu \vec{\mathbf{u}} \, | ||
| + | \right) = | ||
| + | \left( | ||
| + | \, \alpha \mu \, | ||
| + | \right) | ||
| + | \vec{\mathbf{u}} | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Además, si | ||
| + | <math> | ||
| + | \alpha \vec{\mathbf{u}} = \vec{\mathbf{0}} | ||
| + | </math> | ||
| + | , se verifica que | ||
| + | <math> | ||
| + | \alpha = 0 | ||
| + | </math> | ||
| + | o | ||
| + | <math> | ||
| + | \vec{\mathbf{u}} = \vec{\mathbf{0}} | ||
| + | </math> | ||
| + | . | ||
Revisión de 02:47 16 dic 2006
En el plano, un vector fijo
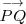 es un segmento orientado de origen
es un segmento orientado de origen
 y extremo
y extremo
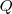 , que tiene las siguientes caracteristicas:
, que tiene las siguientes caracteristicas:
 Módulo: longitud del segmento
Módulo: longitud del segmento
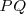 .
.
 Dirección: la de la recta que lo contiene y todas sus paralelas.
Dirección: la de la recta que lo contiene y todas sus paralelas.
 Sentido: el que va del origen al extremo.
Sentido: el que va del origen al extremo.
Los vectores
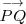 y
y
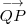 tienen el mismo módulo y la misma dirección, pero sentido contrario.
Los vectores
tienen el mismo módulo y la misma dirección, pero sentido contrario.
Los vectores
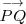 y
y
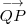 son opuestos.
son opuestos.
El conjunto de todos los vectores fijos del mismo módulo, dirección y sentido forma lo
que se denomina un vector libre. Una propiedad importante que cumplen los vectores libres
es que si
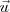 es un vector libre y
es un vector libre y
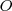 es un punto del plano, existe un único punto
es un punto del plano, existe un único punto
 tal que
tal que
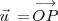 .
.
Componentes de un vector
Un sistema de referencia esta formado por dos rectas
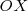 y
y
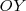 , llamadas ejes de coordenadas que se cortan en un punto
, llamadas ejes de coordenadas que se cortan en un punto
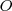 , origen de coordenadas, y una unidad de medida en cada eje. Cuando las dos rectas
son perpendiculares el sistema es ortogonal y cuando, además, las dos unidades de medida
son iguales a uno, el sistema es ortonormal.
, origen de coordenadas, y una unidad de medida en cada eje. Cuando las dos rectas
son perpendiculares el sistema es ortogonal y cuando, además, las dos unidades de medida
son iguales a uno, el sistema es ortonormal.
Para representar un punto
 del plano en un sistema de coordenadas cartesiano
se trazan dese
del plano en un sistema de coordenadas cartesiano
se trazan dese
 perpendiculares a los ejes, obteniendo
perpendiculares a los ejes, obteniendo
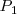 y
y
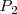 . Si la distancia de
. Si la distancia de
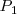 a
a
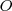 es
es
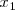 , y la de
, y la de
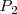 a
a
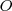 es
es
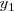 , entonces
, entonces
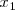 e
e
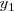 reciben el nombre de coordenadas del punto
reciben el nombre de coordenadas del punto
 . Se escribe
. Se escribe
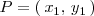 , siendo
, siendo
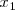 la abcisa e
la abcisa e
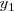 la ordenada.
la ordenada.
Conocidas las coordenadas del origen
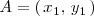 y del extremo
y del extremo
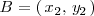 de un vector fijo
de un vector fijo
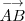 , se puede determinar las componentes del vector restando a las coordenadas del
extremo las del origen:
, se puede determinar las componentes del vector restando a las coordenadas del
extremo las del origen:
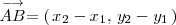
Suma de vectores
Sean
 y
y
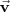 dos vectores libres, se define el vector suma
dos vectores libres, se define el vector suma
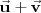 como otro vector obtenido de la siguiente forma:
como otro vector obtenido de la siguiente forma:
1. Se señala un punto
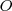 del plano y se traza el vector
del plano y se traza el vector
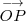 representante de
representante de
 .
.
2. Por el extremo
 se traza el vector
se traza el vector
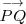
3. El vector
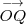 que tiene como origen
que tiene como origen
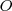 ( origen del primero ) y como extremo
( origen del primero ) y como extremo
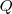 ( extremo del segundo ) es el representante del vector suma
( extremo del segundo ) es el representante del vector suma
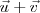 .
.
La suma tiene las siguientes propiedades:
 Asosiativa:
Asosiativa:
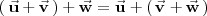
 El vector nulo es
El vector nulo es
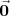 , pues:
, pues:
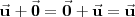
 El vector opuesto de
El vector opuesto de
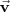 es
es
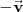 , pues:
, pues:
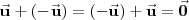
 Conmutativa:
Conmutativa:
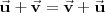
Producto de un número real por un vector
Si
 es un vector libre y
es un vector libre y
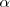 un número real, se define el producto
un número real, se define el producto
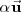 como un nuevo vector qu tiene por módulo el producto
como un nuevo vector qu tiene por módulo el producto
 , por dirección la misma de
, por dirección la misma de
 y sentido el mismo de
y sentido el mismo de
 si
si
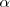 es positivo, y opuesto, si
es positivo, y opuesto, si
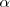 es negativo.
es negativo.
El producto de un número real por un vector tiene las siguientes propiedades:
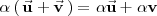
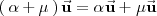
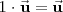
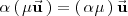
Además, si
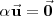 , se verifica que
, se verifica que
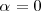 o
o
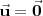 .
.