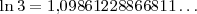Navegación
Conceptos básicos y definición
De Wikillerato
(Página nueva: ==Definición== En matemáticas, los '''números reales''' son aquellos que poseen una expresión decimal e incluyen tanto a los números racionales (como: 31, 37/22, 25,4) como a lo...) |
(→Definición) |
||
| (2 ediciones intermedias no se muestran.) | |||
| Línea 3: | Línea 3: | ||
En matemáticas, los '''números reales''' son aquellos que poseen una expresión decimal e incluyen tanto a los números racionales (como: 31, 37/22, 25,4) como a los números irracionales, que no se pueden expresar de manera fraccionaria y tienen infinitas cifras decimales no periódicas, tales como: <math>\sqrt{2}, \pi</math>. | En matemáticas, los '''números reales''' son aquellos que poseen una expresión decimal e incluyen tanto a los números racionales (como: 31, 37/22, 25,4) como a los números irracionales, que no se pueden expresar de manera fraccionaria y tienen infinitas cifras decimales no periódicas, tales como: <math>\sqrt{2}, \pi</math>. | ||
| - | Pueden ser descritos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal. | + | Pueden ser descritos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal. |
==Historia== | ==Historia== | ||
Durante los siglos XVI y XVII el cálculo avanzó mucho aunque carecía de una base rigurosa, puesto que en el momento no se consideraba necesario el formalismo de la actualidad, y se usaban expresiones como «pequeño», «límite», «se acerca» sin una definición precisa. Esto llevó a una serie de paradojas y problemas lógicos que hicieron evidente la necesidad de crear una base rigurosa para la matemática, la cual consistió de definiciones formales y rigurosas (aunque ciertamente técnicas) del concepto de número real.1 En una sección posterior se describirán dos de las definiciones precisas más usuales actualmente: clases de equivalencia de sucesiones de Cauchy de números racionales y cortaduras de Dedekind. | Durante los siglos XVI y XVII el cálculo avanzó mucho aunque carecía de una base rigurosa, puesto que en el momento no se consideraba necesario el formalismo de la actualidad, y se usaban expresiones como «pequeño», «límite», «se acerca» sin una definición precisa. Esto llevó a una serie de paradojas y problemas lógicos que hicieron evidente la necesidad de crear una base rigurosa para la matemática, la cual consistió de definiciones formales y rigurosas (aunque ciertamente técnicas) del concepto de número real.1 En una sección posterior se describirán dos de las definiciones precisas más usuales actualmente: clases de equivalencia de sucesiones de Cauchy de números racionales y cortaduras de Dedekind. | ||
| - | . | + | |
| + | |||
| + | == Tipos de números reales == | ||
| + | |||
| + | Un número real puede ser un número racional o un número irracional. Los números racionales son aquellos que pueden expresarse como el cociente de dos números enteros, tal como 3/4, -21/3, 5, 0, 1/2, mientras que los irracionales son todos los demaś. Los números racionales también pueden describirse como aquellos cuya representación decimal es eventualmente periódica, mientras que los irracionales tienen una expansión decimal aperiódica: | ||
| + | |||
| + | ; Ejemplos | ||
| + | : 1/4 = 0,25'''0'''0'''0'''0... Es un número racional puesto que es periódico a partir del tercer número decimal. | ||
| + | : 5/7 = 0,'''714285'''714285'''714285'''7.... Es racional y tiene un período de longitud 6 (repite 714285). | ||
| + | :<math>\frac{\sqrt[3]{7}+1}{2}=1\text{,}456465591386194\ldots</math> es irracional y su expansión decimal es aperiódica. | ||
| + | |||
| + | |||
| + | Otra forma de clasificar los números reales es en ''número algebraico|algebraicos'''' y ''número trascendente|trascendentes''. Un número es algebraico si existe un polinomio de coeficientes racionales que lo tiene por raíz y es trascendente en caso contrario. Obviamente, todos los números racionales son algebraicos: si <math>\frac{p}{q}</math> es un número racional, con ''p'' entero y ''q'' natural, entonces es raíz del de la ecuación ''qx''=''p''. Sin embargo, no todos los números algebraicos son racionales. | ||
| + | ; Ejemplos | ||
| + | : El número <math>\frac{\sqrt[3]{7}+1}{2}</math> es algebraico puesto que es la raíz del polinomio <math>8x^3-12x^2+6x-8</math> | ||
| + | : Un ejemplo de número trascendente es <math>\ln3=1\text{,}09861228866811\ldots</math> | ||
| + | |||
[[Categoría:Matemáticas]] | [[Categoría:Matemáticas]] | ||
Revisión actual
Definición
En matemáticas, los números reales son aquellos que poseen una expresión decimal e incluyen tanto a los números racionales (como: 31, 37/22, 25,4) como a los números irracionales, que no se pueden expresar de manera fraccionaria y tienen infinitas cifras decimales no periódicas, tales como: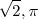 
.
Pueden ser descritos de varias formas, algunas simples aunque carentes del rigor necesario para los propósitos formales de matemáticas y otras más complejas pero con el rigor necesario para el trabajo matemático formal.
Historia
Durante los siglos XVI y XVII el cálculo avanzó mucho aunque carecía de una base rigurosa, puesto que en el momento no se consideraba necesario el formalismo de la actualidad, y se usaban expresiones como «pequeño», «límite», «se acerca» sin una definición precisa. Esto llevó a una serie de paradojas y problemas lógicos que hicieron evidente la necesidad de crear una base rigurosa para la matemática, la cual consistió de definiciones formales y rigurosas (aunque ciertamente técnicas) del concepto de número real.1 En una sección posterior se describirán dos de las definiciones precisas más usuales actualmente: clases de equivalencia de sucesiones de Cauchy de números racionales y cortaduras de Dedekind.
Tipos de números reales
Un número real puede ser un número racional o un número irracional. Los números racionales son aquellos que pueden expresarse como el cociente de dos números enteros, tal como 3/4, -21/3, 5, 0, 1/2, mientras que los irracionales son todos los demaś. Los números racionales también pueden describirse como aquellos cuya representación decimal es eventualmente periódica, mientras que los irracionales tienen una expansión decimal aperiódica:
- Ejemplos
- 1/4 = 0,250000... Es un número racional puesto que es periódico a partir del tercer número decimal.
- 5/7 = 0,7142857142857142857.... Es racional y tiene un período de longitud 6 (repite 714285).
![\frac{\sqrt[3]{7}+1}{2}=1\text{,}456465591386194\ldots](/images/math/math-a2ba25debde8256c3a9ebd554698645c.png "\frac{\sqrt[3]{7}+1}{2}=1\text{,}456465591386194\ldots")
es irracional y su expansión decimal es aperiódica.
Otra forma de clasificar los números reales es en número algebraico|algebraicos'' y número trascendente|trascendentes. Un número es algebraico si existe un polinomio de coeficientes racionales que lo tiene por raíz y es trascendente en caso contrario. Obviamente, todos los números racionales son algebraicos: si 
es un número racional, con p entero y q natural, entonces es raíz del de la ecuación qx=p. Sin embargo, no todos los números algebraicos son racionales.
- Ejemplos
- El número
![\frac{\sqrt[3]{7}+1}{2}](/images/math/math-d49d710ec83058356c80dd5695160d9b.png "\frac{\sqrt[3]{7}+1}{2}")
es algebraico puesto que es la raíz del polinomio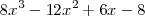 
- Un ejemplo de número trascendente es
