Posiciones relativas de tres planos
De Wikillerato
| Línea 1: | Línea 1: | ||
| + | ==Introduccion== | ||
| + | |||
| + | <br/> | ||
| + | |||
Sean tres planos | Sean tres planos | ||
<math> | <math> | ||
| Línea 87: | Línea 91: | ||
<br/> | <br/> | ||
| - | Según el teorema de Rouché-Frobenius, se pueden | + | Según el teorema de Rouché-Frobenius, se pueden los siguientes casos que pasamos a |
| + | describir en la seccion siguiente. | ||
<br/> | <br/> | ||
| - | + | ==Casos que se pueden dar== | |
| - | + | ||
| - | + | ===Rango ( A ) = Rango ( A | B ) = 3=== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | Rango ( A ) = Rango ( A | B ) = 3 | + | |
| - | + | ||
<br/> | <br/> | ||
| Línea 183: | Línea 182: | ||
<br/> | <br/> | ||
| - | + | ===Rango ( A ) = 2, Rango ( A | B ) = 3=== | |
<br/> | <br/> | ||
| - | + | El sistema de ecuaciones es incompatible, no tiene solucion. Los tres planos no tienen ningún punto en comun. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Puden presentarse dos situaciones distintas: | |
<br/> | <br/> | ||
| - | + | ====Subcaso 2.1==== | |
<br/> | <br/> | ||
| - | |||
| - | |||
| - | |||
| - | |||
Los planos se cortan dos a dos según rectas paralelas. Entre los planos considerados | Los planos se cortan dos a dos según rectas paralelas. Entre los planos considerados | ||
no hay dos que sean paralelos. Por tanto, cada dos planos se cortan según una recta. | no hay dos que sean paralelos. Por tanto, cada dos planos se cortan según una recta. | ||
| Línea 216: | Línea 203: | ||
<br/> | <br/> | ||
| - | + | ====Subcaso 2.2==== | |
| - | + | ||
| - | Subcaso 2.2 | + | <br/> |
| - | </ | + | |
Dos planos paralelos cortados por el tercero. | Dos planos paralelos cortados por el tercero. | ||
<br/> | <br/> | ||
| - | + | Analizando las [[Posiciones relativas de dos planos|posiciones relativas de cada par de | |
| + | planos se cortan según una recta. Son planos]]. | ||
<br/> | <br/> | ||
| - | + | ===Rango ( A ) = Rango ( A | B ) = 2=== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | Rango ( A ) = Rango ( A | B ) = 2 | + | |
| - | + | ||
<br/> | <br/> | ||
| Línea 245: | Línea 225: | ||
<br/> | <br/> | ||
| - | + | ====Subcaso 3.1==== | |
| - | + | ||
| - | Subcaso 3.1 | + | |
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Planos distintos. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | ====Subcaso 3.2==== | |
<br/> | <br/> | ||
| - | + | Dos planos son coincidentes. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | ¿Como distinguir cada uno de estos subcasos? | |
| + | Analizando las [[Posiciones relativas de dos planos|posiciones relativas de cada par de planos]]. | ||
<br/> | <br/> | ||
| - | + | ===Rango ( A ) = 1, Rango ( A | B ) = 2=== | |
<br/> | <br/> | ||
| - | + | El sistema de ecuaciones es incompatible. Los tres planos no tienen ningún punto en común. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | Los tres planos | + | |
<br/> | <br/> | ||
| - | + | Puden presentarse tres situaciones distintas: | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | ====Subcaso 4.1==== | |
| - | + | ||
| - | Subcaso 4. | + | |
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | Los tres planos son paralelos. | |
<br/> | <br/> | ||
| - | + | ====Subcaso 4.2==== | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | + | </span> | |
| + | Dos planos coinciden y el otro es paralelo. | ||
<br/> | <br/> | ||
| - | + | ¿Como distinguir cada uno de estos subcasos? | |
| + | Analizando las [[Posiciones relativas de dos planos|posiciones relativas de cada par de planos]]. | ||
<br/> | <br/> | ||
| - | + | ===Rango ( A ) = Rango ( A | B ) = 1=== | |
| - | + | ||
<br/> | <br/> | ||
| - | + | El sistema de ecuaciones es compatible indeterminado, tiene infinitas soluciones. Los tres planos coinciden. | |
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
| - | + | ||
<br/> | <br/> | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
[[Category:Matemáticas]] | [[Category:Matemáticas]] | ||
Revisión de 00:04 19 dic 2006
Tabla de contenidos |
Introduccion
Sean tres planos
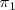 y
y
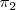 y
y
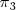 de ecuaciones:
de ecuaciones:
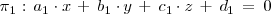
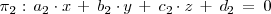
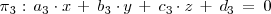
Para determinar sus posiciones relativas, analizamos el sistema formado por las ecuaciones de los tres planos, cuyas matrices asociadas son:
![A \, = \,
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_1 & b_1 & c_1
\\
a_2 & b_2 & c_2
\\
a_3 & b_3 & c_3
\end{array}
</pre>
<p>\right)
A \, = \,
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_1 & b_1 & c_1
\\
a_2 & b_2 & c_2
\\
a_3 & b_3 & c_3
\end{array}
</pre>
<p>\right)](/images/math/math-9eda446dcb1422ac44ab5a2bbd846a37.png)
![A | B \, = \,
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
a_1 & b_1 & c_1
\\
a_2 & b_2 & c_2
\\
a_3 & b_3 & c_3
\end{array}
\right|
\begin{array}[c]{c}
-d_1
\\
-d_2
\\
-d_3
\end{array}
</pre>
<p>\right)
A | B \, = \,
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
a_1 & b_1 & c_1
\\
a_2 & b_2 & c_2
\\
a_3 & b_3 & c_3
\end{array}
\right|
\begin{array}[c]{c}
-d_1
\\
-d_2
\\
-d_3
\end{array}
</pre>
<p>\right)](/images/math/math-6f6dcb913278fc11792ada76f80ed97e.png)
Según el teorema de Rouché-Frobenius, se pueden los siguientes casos que pasamos a describir en la seccion siguiente.
Casos que se pueden dar
Rango ( A ) = Rango ( A | B ) = 3
El sistema de ecuaciones es compatible determinado, y tiene una única solución. Los planos tienen un único punto común. Los planos se cortan en un punto.
Asi, los planos
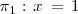
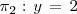
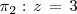
se cortan en el punto
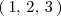 y
y
[Unparseable or potentially dangerous latex formula. Error 3 ]
Rango ( A ) = 2, Rango ( A | B ) = 3
El sistema de ecuaciones es incompatible, no tiene solucion. Los tres planos no tienen ningún punto en comun.
Puden presentarse dos situaciones distintas:
Subcaso 2.1
Los planos se cortan dos a dos según rectas paralelas. Entre los planos considerados no hay dos que sean paralelos. Por tanto, cada dos planos se cortan según una recta.
Subcaso 2.2
Dos planos paralelos cortados por el tercero.
Analizando las posiciones relativas de cada par de planos se cortan según una recta. Son planos.
Rango ( A ) = Rango ( A | B ) = 2
El sistema de ecuaciones es compatible indenterminado, y tiene infinitas soluciones. Los planos se cortan en una reta. Pueden presentarse en este caso dos situciones distintas:
Subcaso 3.1
Planos distintos.
Subcaso 3.2
Dos planos son coincidentes.
¿Como distinguir cada uno de estos subcasos? Analizando las posiciones relativas de cada par de planos.
Rango ( A ) = 1, Rango ( A | B ) = 2
El sistema de ecuaciones es incompatible. Los tres planos no tienen ningún punto en común.
Puden presentarse tres situaciones distintas:
Subcaso 4.1
Los tres planos son paralelos.
Subcaso 4.2
</span> Dos planos coinciden y el otro es paralelo.
¿Como distinguir cada uno de estos subcasos? Analizando las posiciones relativas de cada par de planos.
Rango ( A ) = Rango ( A | B ) = 1
El sistema de ecuaciones es compatible indeterminado, tiene infinitas soluciones. Los tres planos coinciden.



