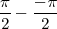Ondas estacionarias sobre una cuerda
De Wikillerato
(Reversión última edición buena) |
|||
| (24 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | |||
| - | |||
==Definición== | ==Definición== | ||
| Línea 31: | Línea 29: | ||
Consideremos una cuerda de longitud L, sujeta por un extremo, sometida a una tensión - si no se ejerce tensión sobre la cuerda no habrá propagación de las ondas- en tanto que en el otro extremo la sometemos a un movimiento vibratorio (Experiencia de Melde) | Consideremos una cuerda de longitud L, sujeta por un extremo, sometida a una tensión - si no se ejerce tensión sobre la cuerda no habrá propagación de las ondas- en tanto que en el otro extremo la sometemos a un movimiento vibratorio (Experiencia de Melde) | ||
| + | |||
| + | |||
| + | [[Imagen:Experiencia-Melde.gif|Experiencia de Melde]] | ||
| + | |||
La segunda figura nos indica cómo veremos la cuerda si la iluminamos con un estroboscopio cuya frecuencia f´ sea 4f, siendo f la frecuencia del vibrador. | La segunda figura nos indica cómo veremos la cuerda si la iluminamos con un estroboscopio cuya frecuencia f´ sea 4f, siendo f la frecuencia del vibrador. | ||
| Línea 37: | Línea 39: | ||
Si consideramos que la recta soporte de las velocidades de propagación fuese el eje x´Ox, una de las ondas se propaga en el sentido creciente de las x y la otra, necesariamente, en el sentido de x decreciente. | Si consideramos que la recta soporte de las velocidades de propagación fuese el eje x´Ox, una de las ondas se propaga en el sentido creciente de las x y la otra, necesariamente, en el sentido de x decreciente. | ||
| + | |||
| + | |||
| + | [[Imagen:curvas-nodos.gif|Formación de nodos]] | ||
| + | |||
Hay puntos del medio en los cuales las ondas se encontrarán en oposición de fase. La superposición de las ondas en esos puntos daría una vibración nula. Los llamaremos nodos de vibración , o simplemente, [[Propiedades_de_las_ondas_estacionarias:_Nodos_y_vientres|nodos]]. | Hay puntos del medio en los cuales las ondas se encontrarán en oposición de fase. La superposición de las ondas en esos puntos daría una vibración nula. Los llamaremos nodos de vibración , o simplemente, [[Propiedades_de_las_ondas_estacionarias:_Nodos_y_vientres|nodos]]. | ||
| Línea 42: | Línea 48: | ||
Escojamos como origen de abcisas uno de esos puntos y un origen de tiempos de tiempos de modo que la ecuación de la elongación <math>y_1</math> , cuando la onda 1 este sola, quede | Escojamos como origen de abcisas uno de esos puntos y un origen de tiempos de tiempos de modo que la ecuación de la elongación <math>y_1</math> , cuando la onda 1 este sola, quede | ||
| - | <math> y_1 =A sen (\omega t + \frac{\pi}{2}\) = A cos\omega t </math> | + | <math> y_1 =A sen (\omega t + \frac{\pi}{2}\)) = A cos\omega t </math> |
| - | Es decir, para t= 0 | + | Es decir, para <math>t = 0 \ \ \ y_1 = A</math> |
| - | <math> y_2 = - A cos\omega t </math> con lo cual para | + | <math>y_2 = - A cos \omega \ t </math> |
| + | |||
| + | con lo cual para <math>t = 0 \ \ \ y_2 = - A</math> | ||
En ese caso la ecuación de la elongación del punto O será la superposición de las elongaciones de las dos ondas y nos da una elongación y = 0, será un nodo de vibración. | En ese caso la ecuación de la elongación del punto O será la superposición de las elongaciones de las dos ondas y nos da una elongación y = 0, será un nodo de vibración. | ||
| Línea 52: | Línea 60: | ||
En un punto M, de abcisa x, encontraremos que la ecuación de los dos frentes de ondas sería: | En un punto M, de abcisa x, encontraremos que la ecuación de los dos frentes de ondas sería: | ||
| - | + | <math>y_1 = A cos(\omega t - k x)</math> | |
| + | |||
| - | + | <math>\left . \begin{matrix}y_2 = -A \cos [ \omega t - k (- x) ] \\y_2 = - A cos (\omega t + k x) \end{matrix} \right \}</math> | |
Con lo cual la elongación del punto M sería: | Con lo cual la elongación del punto M sería: | ||
| - | <math>y = y_1 + y_2 = A | + | <math>y = y_1 + y_2 = A [cos(\omega t - k x) - cos (\omega t + k x)]</math> |
| - | |||
| - | <math>y = - A 2 sen | + | <math>y = - A 2 sen \left( \frac{\omega t - k x + \omega t + k x}{2} \right) sen \left( \frac{\omega t - k x - \omega t - k x}{2} \right)</math> |
| - | |||
| - | <math> y = | + | <math>y = - A \ 2 \ sen \ \omega \ t \ sen (-k x) </math> |
| - | |||
| - | + | pero <math> - sen (-kx) = sen \ kx</math>, entonces | |
| - | <math> | + | |
| + | <math> y = 2A \ sen \ k x \ sen \ \omega t</math> | ||
| + | |||
| + | Ecuación de un movimiento armónico simple. | ||
| + | |||
| + | Todos los puntos de la cuerda estarán vibrando, salvo los nodos, sin que haya un desplazamiento de la fase. | ||
| + | |||
| + | La amplitud resultante, <math>a</math>, será | ||
| + | |||
| + | <math>a = 2A \ sen \ kx</math> | ||
| + | |||
| + | |||
| + | |||
| + | [[Imagen:amplitud.gif|Amplitud]] | ||
| Línea 81: | Línea 100: | ||
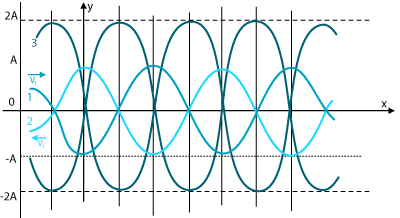
Como resultado de la superposición de las ondas 1 y 2 se obtiene la onda estacionaria 3, cuya amplitud es 2A. | Como resultado de la superposición de las ondas 1 y 2 se obtiene la onda estacionaria 3, cuya amplitud es 2A. | ||
| - | + | ==Nodos y Vientres== | |
| - | Nodos | + | ===Nodos=== |
Se llaman así a los puntos en los que la amplitud es cero. Se caracterizan por sen kx = 0, lo cual se cumple cuando <math>kx = n\pi</math>. | Se llaman así a los puntos en los que la amplitud es cero. Se caracterizan por sen kx = 0, lo cual se cumple cuando <math>kx = n\pi</math>. | ||
| Línea 95: | Línea 114: | ||
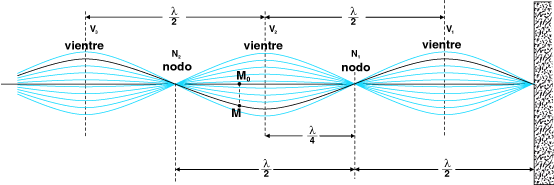
Los nodos de vibración son equidistantes, dos nodos consecutivos distan una semilongitud de onda. | Los nodos de vibración son equidistantes, dos nodos consecutivos distan una semilongitud de onda. | ||
| - | Vientres | + | ===Vientres=== |
Son los puntos del medio donde la amplitud es máxima, es decir, <math>2Asen kx = \pm 1</math> | Son los puntos del medio donde la amplitud es máxima, es decir, <math>2Asen kx = \pm 1</math> | ||
| Línea 107: | Línea 126: | ||
Los vientres son equidistantes, dos vientres consecutivos distan una semilongitud de onda. | Los vientres son equidistantes, dos vientres consecutivos distan una semilongitud de onda. | ||
| - | Consecuencia: La distancia entre un nodo y un vientre consecutivo es un cuarto de longitud de onda. | + | Consecuencia: La distancia entre un nodo y un vientre consecutivo es un cuarto de longitud de onda. |
| + | |||
| + | [[Imagen:Varios-nodos.gif|Vientres y nodos]] | ||
==Fase== | ==Fase== | ||
| Línea 114: | Línea 135: | ||
Podremos decir que una amplitud considerada habitualmente como positiva nos vendrá dada por la expresión: | Podremos decir que una amplitud considerada habitualmente como positiva nos vendrá dada por la expresión: | ||
| - | <math> 2 A \sen (2\pi \frac{x}{lambda}\)</math> | + | <math> 2 A \sen (2\pi \frac{x}{lambda}\))</math> |
La longitud total de la cuerda, L, debe contener un número entero de husos, teniendo en cuenta que cada uso tiene una longitud igual a <math>\frac {\lambda}{2}</math> nos queda <math>L =n \frac {\lambda}{2}</math> | La longitud total de la cuerda, L, debe contener un número entero de husos, teniendo en cuenta que cada uso tiene una longitud igual a <math>\frac {\lambda}{2}</math> nos queda <math>L =n \frac {\lambda}{2}</math> | ||
| Línea 120: | Línea 141: | ||
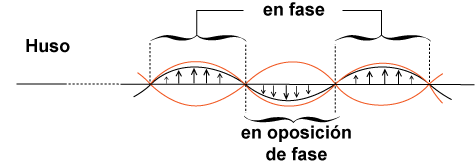
Los puntos del medio que vibran entre dos nodos consecutivos pertenecen al mismo huso tienen igualdad de fase, vibran en fase, se levantan todos a la vez, pasan al mismo tiempo por la posición de equilibrio y bajan todos juntos. En tanto que los puntos que pertenecen a los dos husos vecinos vibran igualmente en fase, pero en oposición de fase con relación a los puntos del huso vecino. | Los puntos del medio que vibran entre dos nodos consecutivos pertenecen al mismo huso tienen igualdad de fase, vibran en fase, se levantan todos a la vez, pasan al mismo tiempo por la posición de equilibrio y bajan todos juntos. En tanto que los puntos que pertenecen a los dos husos vecinos vibran igualmente en fase, pero en oposición de fase con relación a los puntos del huso vecino. | ||
| - | Con lo cual, todos los puntos que se encuentran entre dos nodos consecutivos tienen la misma fase, <math> +\frac{\pi}{2} | + | Con lo cual, todos los puntos que se encuentran entre dos nodos consecutivos tienen la misma fase, <math> +\frac{\pi}{2}</math> o <math> -\frac{\pi}{2}</math> |
Hay estacionareidad de fase, de ahí que se les llame ondas estacionarias. | Hay estacionareidad de fase, de ahí que se les llame ondas estacionarias. | ||
| Línea 128: | Línea 149: | ||
[[Imagen:fase.gif|Fase]] | [[Imagen:fase.gif|Fase]] | ||
| + | |||
| + | [[Categoría: Física]] | ||
Revisión actual
Tabla de contenidos |
Definición
Llamamos onda estacionaria al fenómeno vibratorio de un punto del medio resultante de la superposición de dos ondas progresivas, de igual frecuencia, igual amplitud, pero que se propagan en sentidos opuestos.
Una onda estacionaria ideal es aquella cuya vibración se efectúa sin pérdida ni ganancia de energía, sea por fricción o por emisión radiante, sin que haya propagación de la fase.
Ese estado límite, ideal y conservativo, no se puede encontrar en estado puro salvo en condiciones muy particulares. Como ya veremos, los electrones en un átomo se encuentran en estados estacionarios en el estado de energía fundamental de un átomo.
La realidad, nos permite a menudo observar sistemas casi-estacionarios, que se forman en determinados medios limitados. Sus puntos mantienen siempre el mismo estado de vibración, es decir, no hay propagación de fase, pero su energía se degrada por fricción o por emisión de energía.
Percepción de las ondas estacionarias
Si percibimos el sonido de una cuerda de guitarra, hay pérdida de energía por amortiguamiento y radiación. En efecto, las ondas casi-estacionarias que se forman en la cuerda, ceden energía por medio del puente a la caja, la cual irradia energía mediante una onda sonora.
En la cuerda, observamos también que los puntos donde la vibración tiene amplitud máxima permanecen fijos, así como aquellos en los que la amplitud es cero.
Veremos como casi todas las ondas estacionarias o casi-estacionarias, se encuentran asociados a fenómenos de resonancia.
Las ondas estacionarias se producen en medios limitados (acotados). Como ejemplos podemos poner, la cuerda de una guitarra cerrada por los extremos (clavija y puente), al igual que las de un violín, un tambor, etc un tubo semiabierto como la trompeta, la flauta o el órgano.
Estudio analítico
Cuando estudiamos como se refleja un pulso en una cuerda al encontrar un extremo fijo, observamos que se reflejaba con la misma velocidad y amplitud, pero con un cambio de signo de la elongación.
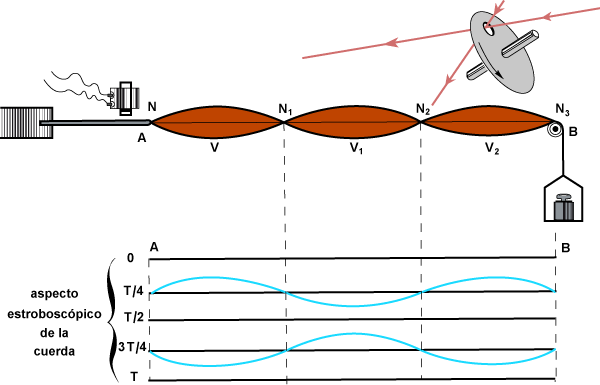
Consideremos una cuerda de longitud L, sujeta por un extremo, sometida a una tensión - si no se ejerce tensión sobre la cuerda no habrá velocidad de propagación de las ondas- en tanto que en el otro extremo la sometemos a un movimiento vibratorio (Experiencia de la cuerda de Melde)
El tren de ondas se refleja en el extremo fijo y se superpone al tren incidente pero con sentido opuesto. Ambos trenes de onda se superponen.
Consideremos una cuerda de longitud L, sujeta por un extremo, sometida a una tensión - si no se ejerce tensión sobre la cuerda no habrá propagación de las ondas- en tanto que en el otro extremo la sometemos a un movimiento vibratorio (Experiencia de Melde)
La segunda figura nos indica cómo veremos la cuerda si la iluminamos con un estroboscopio cuya frecuencia f´ sea 4f, siendo f la frecuencia del vibrador.
Estudiemos en primer lugar, un caso general en el que dos ondas sinusoidales, de la misma pulsación y la misma amplitud, se propagan en la misma dirección y sentido opuesto.
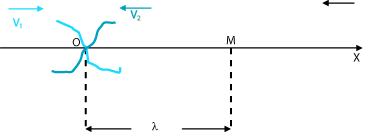
Si consideramos que la recta soporte de las velocidades de propagación fuese el eje x´Ox, una de las ondas se propaga en el sentido creciente de las x y la otra, necesariamente, en el sentido de x decreciente.
Hay puntos del medio en los cuales las ondas se encontrarán en oposición de fase. La superposición de las ondas en esos puntos daría una vibración nula. Los llamaremos nodos de vibración , o simplemente, nodos.
Escojamos como origen de abcisas uno de esos puntos y un origen de tiempos de tiempos de modo que la ecuación de la elongación 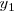 , cuando la onda 1 este sola, quede
, cuando la onda 1 este sola, quede
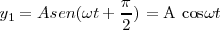
Es decir, para 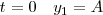
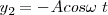
con lo cual para 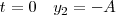
En ese caso la ecuación de la elongación del punto O será la superposición de las elongaciones de las dos ondas y nos da una elongación y = 0, será un nodo de vibración.
En un punto M, de abcisa x, encontraremos que la ecuación de los dos frentes de ondas sería:
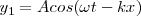
![\left . \begin{matrix}y_2 = -A \cos [ \omega t - k (- x) ] \\y_2 = - A cos (\omega t + k x) \end{matrix} \right \} \left . \begin{matrix}y_2 = -A \cos [ \omega t - k (- x) ] \\y_2 = - A cos (\omega t + k x) \end{matrix} \right \}](/images/math/math-2d98d7fb52056642e0e2e24303d6c053.png)
Con lo cual la elongación del punto M sería:
![y = y_1 + y_2 = A [cos(\omega t - k x) - cos (\omega t + k x)] y = y_1 + y_2 = A [cos(\omega t - k x) - cos (\omega t + k x)]](/images/math/math-fa229258804070b4f48b8ef4c6a275a2.png)
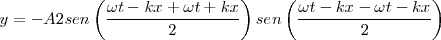
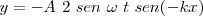
pero 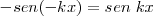 , entonces
, entonces
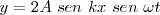
Ecuación de un movimiento armónico simple.
Todos los puntos de la cuerda estarán vibrando, salvo los nodos, sin que haya un desplazamiento de la fase.
La amplitud resultante,  , será
, será
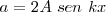
En la figura se representan dos ondas, 1 y 2, que se propagan en sentido opuesto y en el instante inicial, t = 0. En ese instante, las dos ondas están en oposición de fase en el punto 0, donde se produce un nodo.
Como resultado de la superposición de las ondas 1 y 2 se obtiene la onda estacionaria 3, cuya amplitud es 2A.
Nodos y Vientres
Nodos
Se llaman así a los puntos en los que la amplitud es cero. Se caracterizan por sen kx = 0, lo cual se cumple cuando  .
.
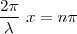 , de donde,
, de donde,
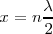 con n perteneciente a N.
con n perteneciente a N.
Los sucesivos nodos de vibración se encontrarán a 0, 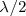 ,
, 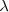 ,
, 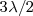 ,…
,…
Los nodos de vibración son equidistantes, dos nodos consecutivos distan una semilongitud de onda.
Vientres
Son los puntos del medio donde la amplitud es máxima, es decir, 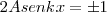
Entonces: 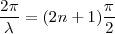
Con lo cual 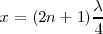
Los sucesivos vientres se encontrarán a  ,
, 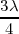 ,
, 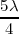 ,
, 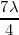 ….
….
Los vientres son equidistantes, dos vientres consecutivos distan una semilongitud de onda.
Consecuencia: La distancia entre un nodo y un vientre consecutivo es un cuarto de longitud de onda.
Fase
Podremos decir que una amplitud considerada habitualmente como positiva nos vendrá dada por la expresión:
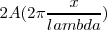
La longitud total de la cuerda, L, debe contener un número entero de husos, teniendo en cuenta que cada uso tiene una longitud igual a  nos queda
nos queda 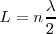
Los puntos del medio que vibran entre dos nodos consecutivos pertenecen al mismo huso tienen igualdad de fase, vibran en fase, se levantan todos a la vez, pasan al mismo tiempo por la posición de equilibrio y bajan todos juntos. En tanto que los puntos que pertenecen a los dos husos vecinos vibran igualmente en fase, pero en oposición de fase con relación a los puntos del huso vecino.
Con lo cual, todos los puntos que se encuentran entre dos nodos consecutivos tienen la misma fase, 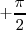 o
o 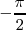
Hay estacionareidad de fase, de ahí que se les llame ondas estacionarias.
La fase varía bruscamente  cuando atravesamos un nodo
cuando atravesamos un nodo