Posiciones relativas de dos rectas
De Wikillerato
(→Coincidentes: Rango ( A ) = Rango ( A | B ) = 2) |
|||
| (47 ediciones intermedias no se muestran.) | |||
| Línea 1: | Línea 1: | ||
| - | |||
| - | |||
==Introducción== | ==Introducción== | ||
| Línea 33: | Línea 31: | ||
s | s | ||
</math> | </math> | ||
| - | | + | cada una de las cuales vienen dada como la interseccion de dos planos: |
<br/> | <br/> | ||
| Línea 123: | Línea 121: | ||
\ge 2 | \ge 2 | ||
</math> | </math> | ||
| - | . Según el teorema de Rouché- | + | . Según el teorema de Rouché-Fröbenius, se pueden presentar los casos que describimos a continuacion. |
<br/> | <br/> | ||
| Línea 135: | Línea 133: | ||
<br/> | <br/> | ||
| - | El sistema de ecuaciones es compatible indeterminado | + | El sistema de ecuaciones es compatible indeterminado ( tiene infinitas |
| - | rectas tienen todos sus puntos comunes. Son '''''rectas coincidentes.''''' | + | soluciones ). Las |
| + | rectas tienen todos sus puntos comunes. Son '''''rectas coincidentes.''''' | ||
| - | <br/> | + | <br/> |
===Paralelas: Rango ( A ) = 2, Rango ( A | B ) = 3=== | ===Paralelas: Rango ( A ) = 2, Rango ( A | B ) = 3=== | ||
| Línea 154: | Línea 153: | ||
<br/> | <br/> | ||
| - | El sistema de ecuaciones es compatible determinado | + | El sistema de ecuaciones es compatible determinado ( tiene una solución única ). Las rectas |
| - | tienen un solo punto común, que es el punto de corte. Son '''''rectas secantes.''''' | + | tienen un solo punto común, que es el punto de corte de ambas rectas. Son '''''rectas secantes.''''' |
<br/> | <br/> | ||
Revisión actual
Tabla de contenidos |
Introducción
Dos rectas pueden adoptar en el espacio las cuatro posiciones relativas siguientes:
1. Coincidentes.
2. Paralelas.
3. Secantes.
4. Rectas que se cruzan.
Supongamos que tenemos dos rectas
 y
y
 cada una de las cuales vienen dada como la interseccion de dos planos:
cada una de las cuales vienen dada como la interseccion de dos planos:
![r:
\left\{
</p>
<pre> \begin{array}[c]{rcl}
a_1 \cdot x \, + \, b_1 \cdot y \, + \, c_1 \cdot z \, + \, d_1 \, = \, 0
\\
a_2 \cdot x \, + \, b_2 \cdot y \, + \, c_2 \cdot z \, + \, d_2 \, = \, 0
\end{array}
</pre>
<p>\right.
\qquad s:
\left\{
</p>
<pre> \begin{array}[c]{rcl}
a_3 \cdot x \, + \, b_3 \cdot y \, + \, c_3 \cdot z \, + \, d_3 \, = \, 0
\\
a_4 \cdot x \, + \, b_4 \cdot y \, + \, c_4 \cdot z \, + \, d_4 \, = \, 0
\end{array}
</pre>
<p>\right.
r:
\left\{
</p>
<pre> \begin{array}[c]{rcl}
a_1 \cdot x \, + \, b_1 \cdot y \, + \, c_1 \cdot z \, + \, d_1 \, = \, 0
\\
a_2 \cdot x \, + \, b_2 \cdot y \, + \, c_2 \cdot z \, + \, d_2 \, = \, 0
\end{array}
</pre>
<p>\right.
\qquad s:
\left\{
</p>
<pre> \begin{array}[c]{rcl}
a_3 \cdot x \, + \, b_3 \cdot y \, + \, c_3 \cdot z \, + \, d_3 \, = \, 0
\\
a_4 \cdot x \, + \, b_4 \cdot y \, + \, c_4 \cdot z \, + \, d_4 \, = \, 0
\end{array}
</pre>
<p>\right.](/images/math/math-af3d8faf36c8a6a95d82f367f6cbeb0b.png)
Para determinar su posición relativa en el espacio tendremos que analizar el sistema formado por las ecuaciones de los cuatro planos, cuyas matrices asociadas son:
![A \, = \,
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_1 & b_1 $ c_1
\\
a_2 & b_2 $ c_2
\\
a_3 & b_3 $ c_3
\\
a_4 & b_4 $ c_4
\\
\end{array}
</pre>
<p>\right)
\qquad \mathrm{y} \qquad A | B \, = \,
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
a_1 & b_1 $ c_1
\\
a_2 & b_2 $ c_2
\\
a_3 & b_3 $ c_3
\\
a_4 & b_4 $ c_4
\\
\end{array}
\right|
\begin{array}[c]{ccc}
-d_1
\\
-d_2
\\
-d_3
\\
-d_4
\\
\end{array}
</pre>
<p>\right)
A \, = \,
\left(
</p>
<pre> \begin{array}[c]{ccc}
a_1 & b_1 $ c_1
\\
a_2 & b_2 $ c_2
\\
a_3 & b_3 $ c_3
\\
a_4 & b_4 $ c_4
\\
\end{array}
</pre>
<p>\right)
\qquad \mathrm{y} \qquad A | B \, = \,
\left(
</p>
<pre> \left.
\begin{array}[c]{ccc}
a_1 & b_1 $ c_1
\\
a_2 & b_2 $ c_2
\\
a_3 & b_3 $ c_3
\\
a_4 & b_4 $ c_4
\\
\end{array}
\right|
\begin{array}[c]{ccc}
-d_1
\\
-d_2
\\
-d_3
\\
-d_4
\\
\end{array}
</pre>
<p>\right)](/images/math/math-5985e3acb7aa748e2bac1137a39082aa.png)
Las dos primeras filas de
 son linealmente independientes, ya que ambos planos determinan una recta. Por
tanto, Rango ( A )
son linealmente independientes, ya que ambos planos determinan una recta. Por
tanto, Rango ( A )
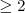 y Rango ( A | B )
y Rango ( A | B )
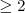 . Según el teorema de Rouché-Fröbenius, se pueden presentar los casos que describimos a continuacion.
. Según el teorema de Rouché-Fröbenius, se pueden presentar los casos que describimos a continuacion.
Casos que se pueden dar:
Coincidentes: Rango ( A ) = Rango ( A | B ) = 2
El sistema de ecuaciones es compatible indeterminado ( tiene infinitas soluciones ). Las rectas tienen todos sus puntos comunes. Son rectas coincidentes.
Paralelas: Rango ( A ) = 2, Rango ( A | B ) = 3
El sistema es incompatible, no tiene solución. Las rectas no tienen ningún punto en común, pero como Rango ( A ) = 2, las rectas son coplanarias ( estan en el mismo plano ). Son rectas paralelas.
Secantes: Rango ( A ) = Rango ( A | B ) = 3
El sistema de ecuaciones es compatible determinado ( tiene una solución única ). Las rectas tienen un solo punto común, que es el punto de corte de ambas rectas. Son rectas secantes.
Rectas que se cruzan: Rango ( A ) = 3, Rango ( A | B ) =4
El sistema es incompatible, no tiene solucion. No tienen ningún punto en común, y como Rango ( A ) = 3, las rectas no son coplanarias ( no estan contenidas en un mismo plano ). Son rectas que se cruzan.
Otro procedimiento para determinar la posicion relativa de dos rectas es el siguiente:
1. Obtenemos dos vectores directores
 y
y
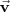 de ambas rectas ( uno de cada recta ).
de ambas rectas ( uno de cada recta ).
2. Si estos son paralelos entonces las rectas son coincidentes o paralelas. Para saber si son coincidentes o paralelas, hallamos un punto en una de las rectas y comprobamos si esta en la otra: si esta, entonces las rectas son coincidentes, si no esta, las rectas son paralelas.
3. Si
 y
y
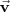 no son paralelos, entonces las rectas son secantes o se cruzan. En este caso,
juntariamos las ecuaciones de las dos rectas y resolveriamos el sistema resultante: si no
tiene solucion, las rectas se cruzan, si tiene solucion, las rectas son secantes.
no son paralelos, entonces las rectas son secantes o se cruzan. En este caso,
juntariamos las ecuaciones de las dos rectas y resolveriamos el sistema resultante: si no
tiene solucion, las rectas se cruzan, si tiene solucion, las rectas son secantes.
Este procedimiento no requiere que las rectas esten dadas como interseccion de dos planos paralelos.



