Distribuciones discretas
De Wikillerato
(Diferencias entre revisiones)
| Línea 1: | Línea 1: | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
__TOC__ | __TOC__ | ||
| Línea 94: | Línea 29: | ||
</math> | </math> | ||
de la variable le hace corresponder la probabilidad de que la variable tome dicho | de la variable le hace corresponder la probabilidad de que la variable tome dicho | ||
| - | valor | + | valor: |
<br/> | <br/> | ||
| Línea 107: | Línea 42: | ||
\mathrm{P} | \mathrm{P} | ||
\left( | \left( | ||
| - | \, X \, = \, x_i\, | + | \, X \, = \, x_i \, |
\right) | \right) | ||
</math> | </math> | ||
| Línea 131: | Línea 66: | ||
<math> | <math> | ||
\sum_{i \, = \, 1}^n \mathrm{f} \left( \, x_i \, \right) \, = \, x_1 \, + \, x_2 \, + \, | \sum_{i \, = \, 1}^n \mathrm{f} \left( \, x_i \, \right) \, = \, x_1 \, + \, x_2 \, + \, | ||
| - | + | \ldots \, + \, x_n | |
</math> | </math> | ||
</center> | </center> | ||
| Línea 145: | Línea 80: | ||
<br/> | <br/> | ||
| - | En el experimento de lanzar tres monedas al aire, la aplicación | + | En el experimento de lanzar tres monedas al aire, la aplicación |
| - | + | ||
<math> | <math> | ||
X | X | ||
</math> | </math> | ||
| - | de cruces obtenidas es una variable aleatoria. En este caso: | + | que asigna a cada resultado el numero de cruces obtenidas es una variable aleatoria. En este caso: |
<br/> | <br/> | ||
| Línea 161: | Línea 95: | ||
\, X \, = \, 0 \, | \, X \, = \, 0 \, | ||
\right) | \right) | ||
| - | \, = \, \frac{1}{8} | + | \, = \, \frac{1}{8} \qquad |
& | & | ||
\mathrm{f} | \mathrm{f} | ||
| Línea 169: | Línea 103: | ||
\, = \, \mathrm{P} | \, = \, \mathrm{P} | ||
\left( | \left( | ||
| - | \, X \, = \, | + | \, X \, = \, 1 \, |
\right) | \right) | ||
\, = \, \frac{3}{8} | \, = \, \frac{3}{8} | ||
| + | \\ | ||
| + | \hline | ||
\\ | \\ | ||
\mathrm{f} \left( \, 2 \, \right) \, = \, \mathrm{P} | \mathrm{f} \left( \, 2 \, \right) \, = \, \mathrm{P} | ||
\left( | \left( | ||
| - | \, X \, = \, | + | \, X \, = \, 2 \, |
\right) | \right) | ||
| - | \, = \, \frac{3}{8} | + | \, = \, \frac{3}{8} \qquad |
& | & | ||
\mathrm{f} \left( \, 3 \, \right) \, = \, \mathrm{P} | \mathrm{f} \left( \, 3 \, \right) \, = \, \mathrm{P} | ||
\left( | \left( | ||
| - | \, X \, = \, | + | \, X \, = \, 3 \, |
\right) | \right) | ||
\, = \, \frac{1}{8} | \, = \, \frac{1}{8} | ||
| Línea 193: | Línea 129: | ||
<math> | <math> | ||
\mathrm{f} \left( \, 0 \, \right) \, + \, \mathrm{f} \left( \, 1 \, \right) \, + \, | \mathrm{f} \left( \, 0 \, \right) \, + \, \mathrm{f} \left( \, 1 \, \right) \, + \, | ||
| - | + | \mathrm{f} \left( \, 2 \, \right) \, + \, \mathrm{f} \left( \, 3 \, \right) \, = \, 1 | |
</math> | </math> | ||
| - | + | ||
| + | <br/> | ||
| + | |||
| + | [[Category:Matemáticas]] | ||
Revisión de 22:19 26 dic 2006
Tabla de contenidos |
Función de probabilidad
Denotaremos como
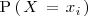 a la probabilidad de que la variable aleatoria tome el valor
a la probabilidad de que la variable aleatoria tome el valor
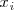 .
.
Se llama función de probabilidad de una variable aleatoria discreta
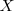 a la aplicacion que a cada valor de
a la aplicacion que a cada valor de
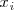 de la variable le hace corresponder la probabilidad de que la variable tome dicho
valor:
de la variable le hace corresponder la probabilidad de que la variable tome dicho
valor:
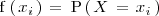
Por definición, deducimos que si
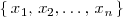 son los valores que puede tomar la variable
son los valores que puede tomar la variable
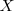 , entonces:
, entonces:
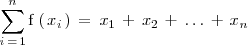
ya que esta suma es, en realidad, la probabilidad del suceso seguro.
Ejemplo
En el experimento de lanzar tres monedas al aire, la aplicación
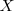 que asigna a cada resultado el numero de cruces obtenidas es una variable aleatoria. En este caso:
que asigna a cada resultado el numero de cruces obtenidas es una variable aleatoria. En este caso:
![\begin{array}[c]{cc}
\mathrm{f} \left( \, 0 \, \right) \, = \, \mathrm{P}
</p>
<pre>\left(
\, X \, = \, 0 \,
\right)
\, = \, \frac{1}{8} \qquad
&
\mathrm{f}
\left(
\, 1 \,
\right)
\, = \, \mathrm{P}
\left(
\, X \, = \, 1 \,
\right)
\, = \, \frac{3}{8}
\\
\hline
\\
\mathrm{f} \left( \, 2 \, \right) \, = \, \mathrm{P}
\left(
\, X \, = \, 2 \,
\right)
\, = \, \frac{3}{8} \qquad
&
\mathrm{f} \left( \, 3 \, \right) \, = \, \mathrm{P}
\left(
\, X \, = \, 3 \,
\right)
\, = \, \frac{1}{8}
</pre>
<p>\end{array}
\begin{array}[c]{cc}
\mathrm{f} \left( \, 0 \, \right) \, = \, \mathrm{P}
</p>
<pre>\left(
\, X \, = \, 0 \,
\right)
\, = \, \frac{1}{8} \qquad
&
\mathrm{f}
\left(
\, 1 \,
\right)
\, = \, \mathrm{P}
\left(
\, X \, = \, 1 \,
\right)
\, = \, \frac{3}{8}
\\
\hline
\\
\mathrm{f} \left( \, 2 \, \right) \, = \, \mathrm{P}
\left(
\, X \, = \, 2 \,
\right)
\, = \, \frac{3}{8} \qquad
&
\mathrm{f} \left( \, 3 \, \right) \, = \, \mathrm{P}
\left(
\, X \, = \, 3 \,
\right)
\, = \, \frac{1}{8}
</pre>
<p>\end{array}](/images/math/math-caa2252e081f8d4cf87c94bbcb0d456d.png)
Observa que