Sistemas de ecuaciones lineales
De Wikillerato
| Línea 132: | Línea 132: | ||
<br/> | <br/> | ||
| - | + | De izquierda a derecha, la primera matriz, en la igualdad anterior es la '''''matriz de los coeficientes''''' y la llamaremos | |
| + | | ||
| + | <math> | ||
| + | A | ||
| + | </math> | ||
| + | , la segunda matriz es la matriz de las incognitas y la llamaremos | ||
| + | <math> | ||
| + | X | ||
| + | </math> | ||
| + | . La tercera es la matriz de los terminos indedependientes y la llamaremos | ||
| + | <math> | ||
| + | B | ||
| + | </math> | ||
| + | . | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | Con esta notación, nuestro sistema de ecuaciones lineales se puede representar de la | ||
| + | siguiente manera: | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | <center> | ||
| + | <math> | ||
| + | A \cdot X \, = \, B | ||
| + | </math> | ||
| + | </center> | ||
| + | |||
| + | <br/> | ||
| + | |||
| + | La | ||
'''''matriz ampliada''''' es la matriz de los coeficientes, | '''''matriz ampliada''''' es la matriz de los coeficientes, | ||
<math> | <math> | ||
| Línea 170: | Línea 200: | ||
\end{array} | \end{array} | ||
\right) | \right) | ||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
| - | |||
</math> | </math> | ||
</center> | </center> | ||
Revisión de 11:34 28 dic 2006
Un sistema de ecuaciones lineales con incógnitas
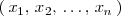 es un conjunto formado por
es un conjunto formado por
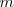 igualdades de la forma:
igualdades de la forma:
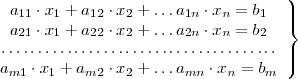
donde los
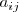 se llaman coeficientes y los
se llaman coeficientes y los
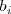 , terminos independientes del sistema.
, terminos independientes del sistema.
En los coeficientes
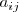 , el subindice
, el subindice
 indica la ecuación del sistema en la que aparece dicho coeficiente, y el subíndice
indica la ecuación del sistema en la que aparece dicho coeficiente, y el subíndice
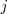 señala de que incognita es coeficiente
señala de que incognita es coeficiente
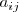 .
.
El subindice
 que aparece en el término
que aparece en el término
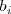 , indica la ecuación de la que
, indica la ecuación de la que
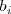 es término independiente.
es término independiente.
El sistema anterior de
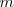 ecuaciones lineales con
ecuaciones lineales con
 incognitas se puede escribir matricialmente de la siguiente forma:
incognitas se puede escribir matricialmente de la siguiente forma:
![\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & a_{1n}
\\
a_{21} & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{c}
x_1
\\
x_2
\\
\vdots
\\
x_n
\end{array}
</pre>
<p>\right)
\, = \,
\left(
</p>
<pre> \begin{array}[c]{c}
b_1
\\
b_2
\\
\vdots
\\
b_m
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & a_{1n}
\\
a_{21} & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right)
\cdot
\left(
</p>
<pre> \begin{array}[c]{c}
x_1
\\
x_2
\\
\vdots
\\
x_n
\end{array}
</pre>
<p>\right)
\, = \,
\left(
</p>
<pre> \begin{array}[c]{c}
b_1
\\
b_2
\\
\vdots
\\
b_m
\end{array}
</pre>
<p>\right)](/images/math/math-5e0cb3bd7b16ad7e059ce5fa38814c2a.png)
De izquierda a derecha, la primera matriz, en la igualdad anterior es la matriz de los coeficientes y la llamaremos
 , la segunda matriz es la matriz de las incognitas y la llamaremos
, la segunda matriz es la matriz de las incognitas y la llamaremos
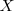 . La tercera es la matriz de los terminos indedependientes y la llamaremos
. La tercera es la matriz de los terminos indedependientes y la llamaremos
 .
.
Con esta notación, nuestro sistema de ecuaciones lineales se puede representar de la siguiente manera:

La
matriz ampliada es la matriz de los coeficientes,
 , a la que se añade la columna de los terminos independientes,
, a la que se añade la columna de los terminos independientes,
 :
:
![A|B \, = \,
\left(
</p>
<pre> \left.
\begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & a_{1n}
\\
a_{21} & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right|
\begin{array}[c]{c}
</p>
<pre> b_1
\\
b_2
\\
\vdots
\\
b_m
</pre>
<p>\end{array}
\right)
A|B \, = \,
\left(
</p>
<pre> \left.
\begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & a_{1n}
\\
a_{21} & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & a_{mn}
\end{array}
</pre>
<p>\right|
\begin{array}[c]{c}
</p>
<pre> b_1
\\
b_2
\\
\vdots
\\
b_m
</pre>
<p>\end{array}
\right)](/images/math/math-f6c1ca9004acfe12b309a46ceb07de9b.png)
Resolver un sistema de ecuaciones lineales es encontrar todas sus soluciones. Al conjunto de todas las soluciones del sistema se le llama solución general, y a cada una de las soluciones que forman dicho conjunto, solución particular.
Serán soluciones del sistema todas las n-tuplas
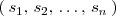 tales que al sustituir
tales que al sustituir
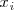 por
por
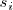 , para
, para
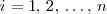 , todas las ecuaciones del sistema se conviertan en identidades.
, todas las ecuaciones del sistema se conviertan en identidades.



