Navegación
Regla de Cramer
De Wikillerato
(Diferencias entre revisiones)
| Línea 4: | Línea 4: | ||
A | A | ||
</math> | </math> | ||
| - | de coeficientes del sistema | + | de coeficientes del sistema es cuadrada y de determinante no nulo. El que |
| - | y de determinante no nulo. El que | + | |
<math> | <math> | ||
A | A | ||
Revisión de 23:11 28 dic 2006
Esta regla es un metodo de resolución de sistemas de ecuaciones lineales que se puede
utilizar cuando la matriz
de coeficientes del sistema es cuadrada y de determinante no nulo. El que
sea cuadrada significa que el numero de incognitas y el numero de ecuaciones
coincide.
Cuando el sistema de ecuaciones
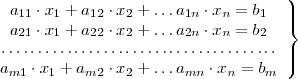
satisface esas condiciones, su solución viene dada por:
![x_1 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
b_1 & a_{12} & \ldots & a_{1n}
\\
b_2 & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
b_m & a_{m2} & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|A|}
, \qquad \qquad x_2 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & b_1 & \ldots & a_{1n}
\\
a_{21} & b_2 & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & b_m & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|A|}, \qquad \qquad \ldots \ldots](/images/math/math-150b5190ce0e6220c11001b683e002fd.png "x_1 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
b_1 & a_{12} & \ldots & a_{1n}
\\
b_2 & a_{22} & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
b_m & a_{m2} & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|A|}
, \qquad \qquad x_2 \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & b_1 & \ldots & a_{1n}
\\
a_{21} & b_2 & \ldots & a_{2n}
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & b_m & \ldots & a_{mn}
\end{array}
\right|
</pre>
<p>}
{|A|}, \qquad \qquad \ldots \ldots")
![\ldots \ldots, \qquad \qquad x_n \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & b_1
\\
a_{21} & a_{22} & \ldots & b_2
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & b_m
\end{array}
\right|
</pre>
<p>}
{|A|}](/images/math/math-d98f027b0fbef3a275e17f38d915d14b.png "\ldots \ldots, \qquad \qquad x_n \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cccc}
a_{11} & a_{12} & \ldots & b_1
\\
a_{21} & a_{22} & \ldots & b_2
\\
\vdots & \vdots & \ddots & \vdots
\\
a_{m1} & a_{m2} & \ldots & b_m
\end{array}
\right|
</pre>
<p>}
{|A|}")
En general
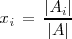
donde
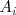es la matriz que se obtiene sustituyendo la i-esima columna de
por matriz de los terminos independientes,
.
Ejemplo
Consideremos el sistema de ecuaciones:
![\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, = \, 2
\\
x \, - \, y \, = \, 0
\end{array}
</pre>
<p>\right.](/images/math/math-9d7fa2a713677bcaf5cea62fe4a5126f.png "\left\{
</p>
<pre> \begin{array}[c]{rcl}
x \, + \, y \, = \, 2
\\
x \, - \, y \, = \, 0
\end{array}
</pre>
<p>\right.")
En este sistema de ecuaciones lineales, la matriz
de los coeficientes es una matriz cuadrada y
![|A| \, = \,
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & ~~1
\\
1 & -1
\end{array}
</pre>
<p>\right|
</p>
<pre>\, = \, -2 \neq 0
</pre>
<p>](/images/math/math-789a2f66f5ebae882988c2ace0979a33.png "|A| \, = \,
\left|
</p>
<pre> \begin{array}[c]{cc}
1 & ~~1
\\
1 & -1
\end{array}
</pre>
<p>\right|
</p>
<pre>\, = \, -2 \neq 0
</pre>
<p>")
. Por lo tanto, podemos aplicar la regla de Cramer para resolverlo:
![x \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
2 & ~~1
\\
0 & -1
\end{array}
\right|
</pre>
<p>}
{|A|} \, = \, \frac{-2}{-2} \, = \, 1
\qquad \qquad y \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
1 & 2
\\
1 & 0
\end{array}
\right|
</pre>
<p>}
{|A|}\, = \, \frac{-2}{-2} \, = \, 1](/images/math/math-8aa774c9773439ba43602bf548f68568.png "x \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
2 & ~~1
\\
0 & -1
\end{array}
\right|
</pre>
<p>}
{|A|} \, = \, \frac{-2}{-2} \, = \, 1
\qquad \qquad y \, = \, \frac
{
</p>
<pre> \left|
\begin{array}[c]{cc}
1 & 2
\\
1 & 0
\end{array}
\right|
</pre>
<p>}
{|A|}\, = \, \frac{-2}{-2} \, = \, 1")
