|
|
| Línea 1: |
Línea 1: |
| - |
| |
| - | ==Definición de matriz==
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Una matriz es un cuadrado o tabla de numeros ordenados. Se llama matriz de dimension
| |
| - |
| |
| - | <math>
| |
| - | m \times n
| |
| - | </math>
| |
| - | a un conjunto de números reales dispuestos en
| |
| - | <math>
| |
| - | m
| |
| - | </math>
| |
| - | filas y
| |
| - | <math>
| |
| - | n
| |
| - | </math>
| |
| - | columnas de la siguiente forma
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{cccc}
| |
| - | a_{11 }& a_{12} & \ldots & a_{1n}
| |
| - | \\
| |
| - | a_{21 }& a_{22} & \ldots & a_{2n}
| |
| - | \\
| |
| - | \vdots & \vdots & \ddots & \vdots
| |
| - | \\
| |
| - | a_{m1 }& a_{m2} & \ldots & a_{mn}
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | La matriz
| |
| - | <math>
| |
| - | A
| |
| - | </math>
| |
| - | se puede designar tambien como
| |
| - | <math>
| |
| - | \quad A = \left( a_{ij} \right) \quad
| |
| - | </math>
| |
| - | donde
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left\{
| |
| - | \begin{array}[c]{l}
| |
| - | i = 1, \, 2, \, \ldots, \, m
| |
| - | \\
| |
| - | j = 1, \, 2, \, \ldots, \, n
| |
| - | \end{array}
| |
| - | \right.
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Un elemento generico de la matriz se designa por
| |
| - | <math>
| |
| - | a_{ij}
| |
| - | </math>
| |
| - | en el cual el subindice
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | representa el numero de fila que ocupa el elemento y el subindice
| |
| - | <math>
| |
| - | j
| |
| - | </math>
| |
| - | el numero de columna.
| |
| - |
| |
| - | El conjunto de matrices de dimension
| |
| - | <math>
| |
| - | m \times n
| |
| - | </math>
| |
| - | se denota por:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | M_{m \times n}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | El conjunto de matrices de dimension
| |
| - | <math>
| |
| - | n \times n
| |
| - | </math>
| |
| - | , tambien llamadas de orden
| |
| - | <math>
| |
| - | n
| |
| - | </math>
| |
| - | , se denota por:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | M_n
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Las matrices de este conjunto se llaman matrices cuadradas y en ellas definimos:
| |
| - |
| |
| - | * la diagonal principal formada por los elementos de la forma
| |
| - | <math>
| |
| - | a_{ii}
| |
| - | </math>
| |
| - |
| |
| - |
| |
| - | *la diagonal secundaria formada por los elementos de la forma
| |
| - | <math>
| |
| - | a_{ij}
| |
| - | </math>
| |
| - | tales que
| |
| - | <math>
| |
| - | i + j = n + 1
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | [[Image:diagonales2.gif]]
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Una '''''matriz rectangular''''' es aquella que tiene distinto número de filas que de columnas
| |
| - |
| |
| - | <math>
| |
| - | \left(
| |
| - | m \neq n
| |
| - | \right)
| |
| - | </math>
| |
| - | .
| |
| - |
| |
| - | ====Ejemplo de matriz rectangular====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 1 & -1 & ~~0
| |
| - | \\
| |
| - | 2 & ~~3 & -1
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''''Matriz fila''''' es toda matriz rectangular con una sola fila de dimension
| |
| - | <math>
| |
| - | 1 \times n
| |
| - | </math>
| |
| - | .
| |
| - |
| |
| - | ====Ejemplo de matriz fila====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | -1 & 3 & 5
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''''Matriz columna''''' es toda matriz rectangular con una sola columna de dimension
| |
| - | <math>
| |
| - | m \times 1
| |
| - | </math>
| |
| - | .
| |
| - |
| |
| - | ====Ejemplo de matriz columna====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{c}
| |
| - | -1
| |
| - | \\
| |
| - | ~~3
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Una '''''matriz nula''''' es una matriz rectangular con todos sus elementos nulos. Se denota
| |
| - | por
| |
| - | <math>
| |
| - | \mathbf{0}
| |
| - | </math>
| |
| - | .
| |
| - |
| |
| - | ====Ejemplo de matriz nula====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 0 & 0 & 0
| |
| - | \\
| |
| - | 0 & 0 & 0
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''''Matriz triangular superior''''' es toda matriz cuadrada en la que todos los terminos
| |
| - | situados por debajo de la diagonal principal son ceros.
| |
| - |
| |
| - | ====Ejemplo de matriz triangular superior====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 1 & -1 & ~~0
| |
| - | \\
| |
| - | 0 & ~~3 & -1
| |
| - | \\
| |
| - | 0 & ~~0 & ~~2
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''''Matriz triangular inferior''''' es toda matriz cuadrada en la que todos los terminos
| |
| - | situados por encima de la diagonal principal son ceros.
| |
| - |
| |
| - | ====Ejemplo de matriz triangular inferior====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 2 & ~~0 & 0
| |
| - | \\
| |
| - | 3 & -1 & 0
| |
| - | \\
| |
| - | 1 & -1 & 3
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''''Matriz diagonal''''' es toda matriz cuadrada en la que todos los terminos
| |
| - | no situados en la diagonal principal son ceros.
| |
| - |
| |
| - | ====Ejemplo de matriz diagonal====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | ~~2 & ~~0 & ~~0
| |
| - | \\
| |
| - | ~~0 & -1 & ~~0
| |
| - | \\
| |
| - | ~~0 & ~~0 & ~~3
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''''Matriz escalar''''' es toda matriz diagonal en la que todos los terminos
| |
| - | de la diagonal principal son iguales.
| |
| - |
| |
| - | ====Ejemplo de matriz escalar====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 2 & {0} & {0}
| |
| - | \\
| |
| - | {0} & 2 & {0}
| |
| - | \\
| |
| - | {0} & {0} & 2
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | '''''Matriz unidad o identidad''''' es la matriz escalar cuyos elementos de la diagonal principal son
| |
| - | todos 1.
| |
| - |
| |
| - | ====Ejemplo de matriz unidad====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 1 & {0} & {0}
| |
| - | \\
| |
| - | {0} & 1 & {0}
| |
| - | \\
| |
| - | {0} & {0} & 1
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | [[Category:Matemáticas]]
| |
| - |
| |
| - | %% }}}
| |
| - | %% {{{ =Operaciones elementales con matrices
| |
| - |
| |
| - | ==Suma de matrices==
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Para dos matrices
| |
| - | <math>
| |
| - | A = \left( a_{ij} \right)
| |
| - | </math>
| |
| - | y
| |
| - | <math>
| |
| - | B = \left( b_{ij} \right)
| |
| - | </math>
| |
| - | de la misma dimension
| |
| - | <math>
| |
| - | m \times n
| |
| - | </math>
| |
| - | , la suma de
| |
| - | <math>
| |
| - | A
| |
| - | </math>
| |
| - | y
| |
| - | <math>
| |
| - | B
| |
| - | </math>
| |
| - | es la matriz de la misma dimension
| |
| - | <math>
| |
| - | m \times n
| |
| - | </math>
| |
| - | , dada por
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A + B = \left( a_{ij} \right) + \left( b_{ij} \right) = \left( a_{ij} + b_{ij} \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A + B =
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | a_{11 }& a_{12} & a_{13}
| |
| - | \\
| |
| - | a_{21 }& a_{22} & a_{23}
| |
| - | \\
| |
| - | a_{31 }& a_{32} & a_{33}
| |
| - | \end{array}
| |
| - | \right)
| |
| - | +
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | b_{11 }& b_{12} & b_{13}
| |
| - | \\
| |
| - | b_{21 }& b_{22} & b_{23}
| |
| - | \\
| |
| - | b_{31 }& b_{32} & b_{33}
| |
| - | \end{array}
| |
| - | \right)
| |
| - | =
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | a_{11 } + b_{11 } & a_{12} + b_{12} & a_{13} + b_{13}
| |
| - | \\
| |
| - | a_{21 } + b_{21 } & a_{22} + b_{22} & a_{23} + b_{23}
| |
| - | \\
| |
| - | a_{31 } + b_{31 } & a_{32} + b_{32} & a_{33} + b_{33}
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ===Propiedades de la suma de matrices===
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 1. Asociativa
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A +
| |
| - | \left(
| |
| - | B + C
| |
| - | \right)
| |
| - | =
| |
| - | \left(
| |
| - | A + B
| |
| - | \right)
| |
| - | + C
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 2. Elemento neutro. La matriz nula,
| |
| - | <math>
| |
| - | 0,
| |
| - | </math>
| |
| - | de la dimension correspondiente es el elemento neutro para la suma, ya que:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A + 0 = 0 + A = A
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 3. Elemento opuesto. Para la matriz
| |
| - | <math>
| |
| - | A
| |
| - | </math>
| |
| - |
| |
| - | existe otra matriz que denotamos por
| |
| - | <math>
| |
| - | -A
| |
| - | </math>
| |
| - | y que llamamos matriz opuesta de
| |
| - | <math>
| |
| - | A,
| |
| - | </math>
| |
| - | que cumple:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A +
| |
| - | \left(
| |
| - | -A
| |
| - | \right)
| |
| - | = 0
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 4. Comutativa
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A + B = B + A
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ==Producto de un numero por una matriz==
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Para un número real
| |
| - | <math>
| |
| - | k
| |
| - | </math>
| |
| - | y una matriz
| |
| - | <math>
| |
| - | A = \left( a_{ij} \right)}
| |
| - | </math>
| |
| - | de dimension
| |
| - | <math>
| |
| - | m \times n
| |
| - | </math>
| |
| - | , el producto de un número real por una matriz es la matriz de la misma dimension
| |
| - |
| |
| - | <math>
| |
| - | m \times n
| |
| - | </math>
| |
| - | dada por
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | k \cdot A = k \cdot \left( a_{ij} \right) = \left( k \cdot a_{ij} \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Es decir, el producto
| |
| - | <math>
| |
| - | k \cdot A
| |
| - | </math>
| |
| - | se obtiene multiplicando el numero real por cada uno de los elementos de la
| |
| - | matriz.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | k \cdot A = k \cdot
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | a_{11 }& a_{12}
| |
| - | \\
| |
| - | a_{21 }& a_{22}
| |
| - | \\
| |
| - | a_{31 }& a_{32}
| |
| - | \end{array}
| |
| - | \right)
| |
| - | =
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | k \cdot a_{11 }& k \cdot a_{12}
| |
| - | \\
| |
| - | k \cdot a_{21 }& k \cdot a_{22}
| |
| - | \\
| |
| - | k \cdot a_{31 }& k \cdot a_{32}
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ==Producto de matrices==
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | El producto de dos matrices
| |
| - | <math>
| |
| - | A = \left( a_{ij} \right)
| |
| - | </math>
| |
| - | de dimension
| |
| - | <math>
| |
| - | m \times n
| |
| - | </math>
| |
| - | y
| |
| - | <math>
| |
| - | B = \left( b_{ij} \right)
| |
| - | </math>
| |
| - | de dimension
| |
| - | <math>
| |
| - | n \times p
| |
| - | </math>
| |
| - | , es la matriz
| |
| - | <math>
| |
| - | A \cdot B
| |
| - | </math>
| |
| - | dada por:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A \cdot B = \left( c_{ij} \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | con
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | c_{ij} = \sum_{j = 1}^n a_{ij} \cdot b_{jk}
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Es decir, cada elemento
| |
| - | <math>
| |
| - | c_{ik}
| |
| - | </math>
| |
| - | se obtiene multiplicando la fila i-ésima de la primera matriz por la columna
| |
| - | k-ésima de la segunda matriz.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{ccc}
| |
| - | 1 & 2 & 3
| |
| - | \\
| |
| - | 4 & 5 & 6
| |
| - | \end{array}
| |
| - | \right)
| |
| - | \cdot
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | ~~7 & ~~8
| |
| - | \\
| |
| - | ~~9 & ~~0
| |
| - | \\
| |
| - | -1 & -2
| |
| - | \end{array}
| |
| - | \right)
| |
| - | =
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | 1 \cdot 7 + 2 \cdot 9 + 3 \cdot \left( -1 \right) & 1 \cdot 8 + 2 \cdot 0 + 3 \cdot \left( -2 \right)
| |
| - | \\
| |
| - | 4 \cdot 7 + 5 \cdot 9 + 6 \cdot \left( -1 \right) & 4 \cdot 8 + 5 \cdot 0 + 6 \cdot \left( -2 \right)
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ===Propiedades del producto de matrices===
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 1. El producto de matrices cuadradas es asociativo:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A \cdot
| |
| - | \left(
| |
| - | B \cdot C
| |
| - | \right)
| |
| - | =
| |
| - | \left(
| |
| - | A \cdot B
| |
| - | \right)
| |
| - | \cdot C
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 2. El producto de matrices cuadradas de orden
| |
| - | <math>
| |
| - | n
| |
| - | </math>
| |
| - | posee como elemento neutro la matriz unidad o identidad
| |
| - | <math>
| |
| - | I
| |
| - | </math>
| |
| - | de orden
| |
| - | <math>
| |
| - | n
| |
| - | </math>
| |
| - | ya que:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A \cdot I = I \cdot A = A
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 3. El producto de matrices cuadradas es distributivo respecto de la suma de matrices:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A \cdot
| |
| - | \left(
| |
| - | B + C
| |
| - | \right)
| |
| - | = A \cdot B + A \cdot C
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | [[Category:Matemáticas]]
| |
| - | %% }}}
| |
| - | %% {{{ =Matriz transpuesta
| |
| - |
| |
| | ==Definición== | | ==Definición== |
| | | | |
| Línea 880: |
Línea 125: |
| | | | |
| | [[Category:Matemáticas]] | | [[Category:Matemáticas]] |
| - |
| |
| - | %% }}}
| |
| - | %% {{{ =Matriz inversa
| |
| - |
| |
| - | __TOC__
| |
| - |
| |
| - | ==Definición==
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | La matriz inversa de una matriz cuadrada
| |
| - | <math>
| |
| - | A
| |
| - | </math>
| |
| - | de orden
| |
| - | <math>
| |
| - | n,
| |
| - | </math>
| |
| - | es la matriz,
| |
| - | <math>
| |
| - | A^{-1}
| |
| - | </math>
| |
| - | , de orden
| |
| - | <math>
| |
| - | n
| |
| - | </math>
| |
| - | que verifica:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A \cdot A^{-1} = A^{-1} \cdot A = I
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | donde
| |
| - | <math>
| |
| - | I
| |
| - | </math>
| |
| - | es la matriz identidad de orden
| |
| - | <math>
| |
| - | n
| |
| - | </math>
| |
| - | .
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Las matrices que tienen inversas se llaman regulares y las que no tienen inversa matrices
| |
| - | singulares.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Las propiedades más importantes relativas a la matriz inversa:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 1. Si existe,
| |
| - | <math>
| |
| - | A^{-1}
| |
| - | </math>
| |
| - | es única.
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 2.
| |
| - | <math>
| |
| - | \left(
| |
| - | A^{-1}
| |
| - | \right)
| |
| - | ^{-1} = A
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 3.
| |
| - | <math>
| |
| - | \left(
| |
| - | A \cdot B
| |
| - | \right)
| |
| - | ^{-1} = B^{-1} \cdot A^{-1}
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ==Cálculo de la matriz inversa==
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Para calcular la matriz inversa de una matriz regular podemos utilizar dos procedimientos:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ===Mediante la definicion===
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Ejemplo====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A =
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | 1 & 2
| |
| - | \\
| |
| - | 3 & 7
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | hacemos
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | A^{-1} =
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | a & b
| |
| - | \\
| |
| - | c & d
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | como
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | I = A \cdot A^{-1} \Rightarrow
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | 1 & 2
| |
| - | \\
| |
| - | 3 & 7
| |
| - | \end{array}
| |
| - | \right)
| |
| - | \cdot
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | a & b
| |
| - | \\
| |
| - | c & d
| |
| - | \end{array}
| |
| - | \right)
| |
| - | =
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | 1 & 0
| |
| - | \\
| |
| - | 0 & 1
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Operando:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | a + 2c & b + 2d
| |
| - | \\
| |
| - | 3a + 7c & 3b + 7d
| |
| - | \end{array}
| |
| - | \right)
| |
| - | =
| |
| - | \left(
| |
| - | \begin{array}[c]{cc}
| |
| - | 1 & 0
| |
| - | \\
| |
| - | 0 & 1
| |
| - | \end{array}
| |
| - | \right)
| |
| - | \Leftrightarrow
| |
| - | \left\{
| |
| - | \begin{array}[c]{ccc}
| |
| - | a + 2c & = & 1
| |
| - | \\
| |
| - | 3a + 7c & = & 0
| |
| - | \\
| |
| - | b + 2d & = & 0
| |
| - | \\
| |
| - | 3b + 7d & = & 1
| |
| - | \\
| |
| - | \end{array}
| |
| - | \right.
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \Rightarrow \left\{
| |
| - | \begin{array}[c]{ccc}
| |
| - | a & = & 7
| |
| - | \\
| |
| - | b & = & -2
| |
| - | \\
| |
| - | c & = & -3
| |
| - | \\
| |
| - | d & = & 1
| |
| - | \\
| |
| - | \end{array}
| |
| - | \right.
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ===Método de Gauss-Jordan===
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | La inversa de una matriz regular
| |
| - | <math>
| |
| - | A
| |
| - | </math>
| |
| - | se calcular transformando la matriz
| |
| - | <math>
| |
| - | \left(
| |
| - | \, A \, \left| \, I \, \right.
| |
| - | \right)
| |
| - | </math>
| |
| - | mediante operaciones elementales por filas en la matriz
| |
| - | <math>
| |
| - | \left(
| |
| - | \, I \, \left| \, A^{-1} \, \right.
| |
| - | \right)
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | ====Operaciones elementales por filas en una matriz====
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Las operaciones elementales por filas en una matriz son las siguientes:
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 1. Intercambiar las filas
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | y
| |
| - | <math>
| |
| - | j,
| |
| - | </math>
| |
| - | que designaremos por
| |
| - | <math>
| |
| - | F_i \longrightarrow F_j
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 2. Multiplicar la fila
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | por el numero
| |
| - | <math>
| |
| - | k \neq 0
| |
| - | </math>
| |
| - | y sustituirla por el resultado; lo designamos por
| |
| - | <math>
| |
| - | F_i \to k \cdot F_i
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 3. Multiplicar la fila
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | por el numero
| |
| - | <math>
| |
| - | k \neq 0
| |
| - | </math>
| |
| - | y sustituirla por el resultado; lo designamos por
| |
| - | <math>
| |
| - | F_i \to k \cdot F_i
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | 4. Sumar las filas
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | y
| |
| - | <math>
| |
| - | j,
| |
| - | </math>
| |
| - | , multiplicadas por sendos números, y llevar el resultado a la fila
| |
| - | <math>
| |
| - | i
| |
| - | </math>
| |
| - | o
| |
| - | <math>
| |
| - | j
| |
| - | </math>
| |
| - | . Lo designamos por
| |
| - | <math>
| |
| - | F_i
| |
| - | </math>
| |
| - | o
| |
| - | <math>
| |
| - | F_j \to k \cdot F_i + t \cdot F_j
| |
| - | </math>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | [[Category:Matemáticas]]
| |
| - |
| |
| - | %% }}}
| |
| - | %% {{{ =Rango de una matriz
| |
| - |
| |
| - | En la matriz
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \begin{array}[c]{cccc}
| |
| - | a_{11 }& a_{12} & \ldots & a_{1n}
| |
| - | \\
| |
| - | a_{21 }& a_{22} & \ldots & a_{2n}
| |
| - | \\
| |
| - | \vdots & \vdots & \ddots & \vdots
| |
| - | \\
| |
| - | a_{m1 }& a_{m2} & \ldots & a_{mn}
| |
| - | \end{array}
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | Se dice que las filas
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | F_i, \, F_j, \, F_k, \, \ldots, \, F_t
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | \left(
| |
| - | \, F_i =
| |
| - | \left(
| |
| - | \, a_{i1 }, \, a_{i2}, \, \ldots, \, a_{in} \,
| |
| - | \right)
| |
| - | \right)
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | son dependientes si existen números
| |
| - | <math>
| |
| - | \alpha_j, \, \alpha_k, \, \ldots, \, \alpha_t \in R
| |
| - | </math>
| |
| - | tales que
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | <center>
| |
| - | <math>
| |
| - | F_i = \alpha_j \cdot F_j + \alpha_k \cdot F_k + \, \ldots \, + \alpha_t \cdot F_t
| |
| - | </math>
| |
| - | </center>
| |
| - |
| |
| - | <br/>
| |
| - |
| |
| - | En caso contrario, se dice que las filas
| |
| - | <math>
| |
| - | F_i, \, F_j, \, F_k, \, \ldots, \, F_t
| |
| - | </math>
| |
| - | son linealmente independientes.
| |
| - |
| |
| - | El '''rango''' de una matriz es el número de filas o de columnas linealmente independientes
| |
| - | que tiene esa matriz.
| |
 de dimension
de dimension
 , a la matriz que se obtiene al cambiar en
, a la matriz que se obtiene al cambiar en
 las filas por columnas o las columnas por filas. Se representa por
las filas por columnas o las columnas por filas. Se representa por
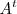 y su dimension es
y su dimension es
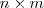
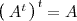
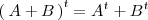
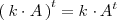
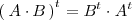
 que coincide con su transpuesta:
que coincide con su transpuesta:
 .
En una matriz simetrica cualquier par de elementos simetricos respecto a la
diagonal principal son iguales.
.
En una matriz simetrica cualquier par de elementos simetricos respecto a la
diagonal principal son iguales.
![\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
2 & 4 & 5
\\
3 & 5 & 7
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{ccc}
1 & 2 & 3
\\
2 & 4 & 5
\\
3 & 5 & 7
\end{array}
</pre>
<p>\right)](/images/math/math-707d3163e2789bbadd06f90a3c397c08.png)
 que coincide con la opuesta de su transpuesta:
que coincide con la opuesta de su transpuesta:
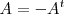 .
En una matriz simetrica cualquier par de elementos simetricos respecto a la
diagonal principal son opuestos.
.
En una matriz simetrica cualquier par de elementos simetricos respecto a la
diagonal principal son opuestos.
![\left(
</p>
<pre> \begin{array}[c]{ccc}
~~ 0 & ~~2 & -3
\\
-2 & ~~0 & ~~5
\\
~~ 3 & -5 & ~~0
\end{array}
</pre>
<p>\right)
\left(
</p>
<pre> \begin{array}[c]{ccc}
~~ 0 & ~~2 & -3
\\
-2 & ~~0 & ~~5
\\
~~ 3 & -5 & ~~0
\end{array}
</pre>
<p>\right)](/images/math/math-790d68307dd50a5291399ef733c5b199.png)



